Ackley no.4 Function

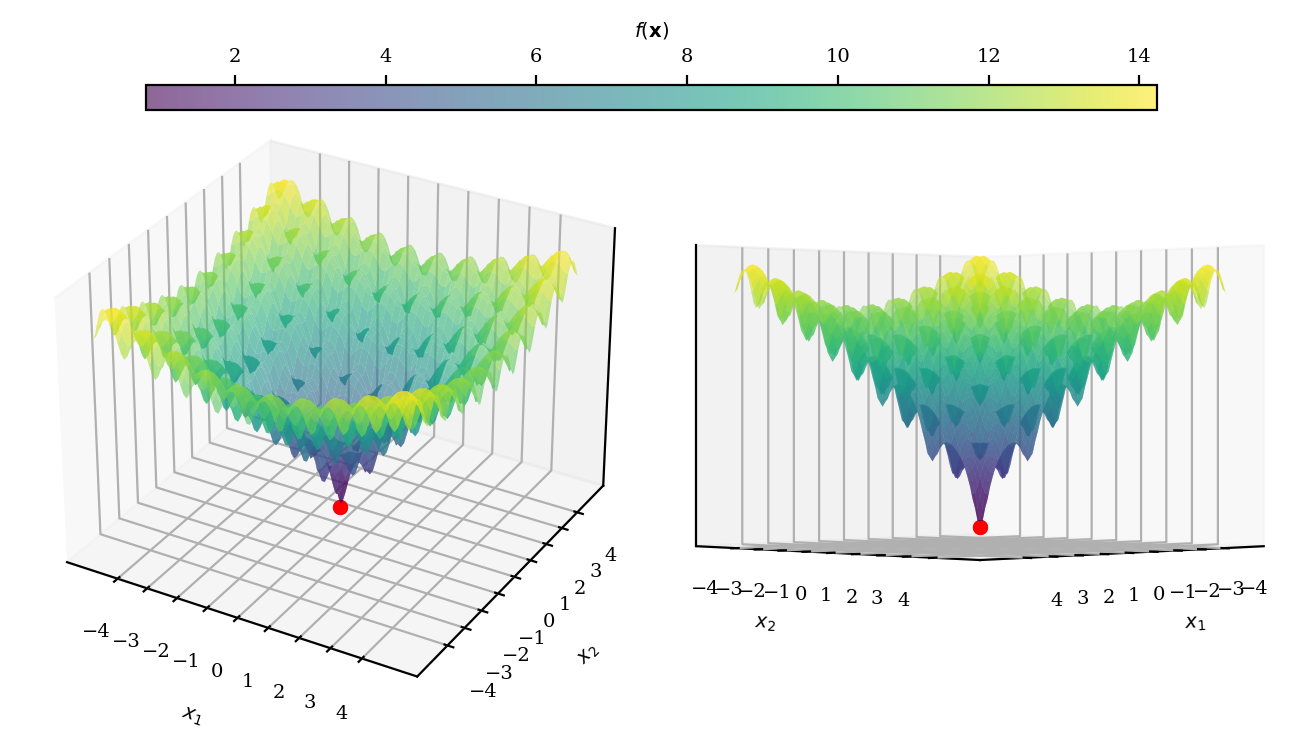
The Ackley no.4 function is a non-continuous, non-convex, non-separable, differentiable, multimodal function often used to assess the performance of optimization algorithms.

./images/example_ackley.png

Python code

> The complete python code for the example can be found in ./examples/example_ackley.py

1. Import required libraries and the optimizers:

from QOPT.QuantumPSO import QuantumPSO
from QOPT.QuantumPMSO import QuantumPMSO
import numpy as np

2. Define the Ackley function:

def ackley(x):
    x = np.array(x)
    return -20 * np.exp(-0.2 * np.sqrt(1. / len(x) * np.sum(x** 2))) - np.exp(
        1. / len(x) * np.sum(np.cos(2 * np.pi * x))) + 20 + np.e

With the current implementation the function has its minimum at $\textbf{x}=[0,0]$.

3. Set up the optimizers and run the optimization:

NParticle = 40
maxiter = 100
NDim = 2
lb = np.array([-5,-5]) ; ub = np.array([5,5])

alpha_min = 0.5
alpha_max = 1.0
sampling = 'LHS'

nworker = 1

# Quantum-behaved Particle Swarm Optimization
optimizer1 = QuantumPSO(
    function=ackley, 
    nparticles=NParticle, 
    dim = NDim,
    lower_bound=lb, 
    upper_bound=ub, 
    maxiter=maxiter, 
    sampling_method = sampling,
    alpha_min=alpha_min, 
    alpha_max=alpha_max,
    nworkers=nworker, 
    tolerance=1e-6, 
    maxiter_below_tolerance=30,
    particle_type = 'Sun-Type1')
optimizer1.update()

# Quantum-behaved Particle Multi-Swarm Optimization
NParticle = 20
nswarms = 2
beta_min = 0.1
beta_max = 0.8
optimizer2 = QuantumPMSO(
    function=ackley, 
    nparticles=NParticle, 
    dim = NDim,
    lower_bound=lb, 
    upper_bound=ub, 
    maxiter=maxiter, 
    sampling_method = sampling,
    alpha_min=alpha_min, 
    alpha_max=alpha_max,
    beta_min=beta_min, 
    beta_max=beta_max,
    nworkers=nworker, 
    tolerance=1e-6, 
    maxiter_below_tolerance=30,
    nswarms=nswarms)
optimizer2.update()