SANISAND

Parameters
1. Optional parameters
Bounds
Constraints
Usage
1. Estimation of $e_0$, $\phi_c$ and $\lambda_c$ from undrained monotonic triaxial tests
Constitutive Equations
References

Parameters

$p_{atm}$ - key: patm - provided in kPa, in most cases $p_{atm}=100$ kPa is valid.
$M_e$ - key: Me
$M_c$ - key: Mc
$\lambda_c$ - key: lambdac
$e_0$ - key: e0
$\xi$ - key: xi
$G_0$ - key: G0
$\nu$ - key: nu
$m$ - key: m
$n_b$ - key: nb
$h_0$ - key: h0
$c_h$ - key: ch
$n_d$ - key: nd
$A_0$ - key: A0
$z_{max}$ - key: zmax
$c_z$ - key: cz

Note that the model does not directly respect the critical state defined by $M_c$ and $M_e$ but rather one defined by $(1+m) M_c$ and $(1+m) M_e$

The numgeo input key for the Sanisand model is:

*Mechanical = Sanisand-2
patm, ec0, lambda, xi, Mc, Me, m, G0
nu, h0, ch, nb, A0, nd, zmax, cz

Optional parameters

Optional parameters offer advanced users more flexibility in choosing amongst different implementation strategies. None of these parameters is mandatory. To change the default values of one or more optional parameters use the keyword *Optional mechanical parameter followed by one ore more of the parameters listed below (default values are given with the keyword):

bulk_water, 0.0 - Bulk modulus of pore water $K^w$ for locally undrained simulations $tr(\dot{\boldsymbol{\varepsilon}})=0$. For any value of $K^w > 0$ the rate of pore water pressure is calculated as follows $\dot{p}^w = - K^w tr(\dot{\boldsymbol{\varepsilon}}) (1+e)/e$. The constitutive behaviour is governed by the effective stress $\boldsymbol{\sigma} = \boldsymbol{\sigma}^{tot}-p^w \boldsymbol{\delta}$, where $\boldsymbol{\sigma}^{tot}$ is the total stress and $\boldsymbol{\delta}$ is the Kronecker delta.
integration, 1 - Method for numerical integration. 1 = Modified-Euler, 2 = Forward Euler
min_pressure, 0.01 - Minimum mean effective stress in kPa (compression = positive).
tol_stress, 1d-4 - Tolerance for stress error in modified-Euler scheme (ignored for Forward Euler)
minimum_dh, 1d-6 - Modified Euler: Minimum size of subincrement, Forward Euler: target strain increment for the calculation of number of subincrements
tangent_stiffness, 2 - When the contribution of the constitutive model $J=\dfrac{\partial \sigma}{\partial \varepsilon}$ to the element stiffness is computed. 1 = tangent stiffness (evaluated at the end of the increment for the updated stress state, default), 2 = “consistent” stiffness (evaluated at the end of each subincrement, a weighted average is returned to the element).
jacobi, 1 - 1 = elastic jacobi, 2 = elaso-plastic tangent, 3 = num-diff jacobi O(h), 4 = num-diff jacobi O(h^2)
tol_yield, 1d-9 - Tolerance for yield surface. Default is $10^{-9}$
drift_correction, 0 - Method for drift correction: 0 = map yield surface by adjusting $\boldsymbol{\alpha}$, 1 = projection along deviatoric plane, else = OpenSees drift correction
drift_maxiter, 50 - Maximum number of iterations for drift correction (only for the OpenSees drift correction, ignored otherwise).
maximum_voidratio, 0.0- Maximum allowed void ratio $e^{max}$ (off per default). If active (for any value larger than zero), $e=min(e,e^{max})$ is enforced.
minimum_voidratio, 0.0- Minimum allowed void ratio $e^{min}$ (off per default). If active (for any value larger than zero), $e=max(e,e^{min})$ is enforced.
force_elastic, 0 - Enforce elastic response, 0 = no, 1 = yes
update_alpha, 1 - Method for the update of $\boldsymbol{\alpha}_\text{ini}$ according to Section Constitutive Equations

Bounds

Per default, we use the following bounds for Sanisand:

$100 \leq p_{atm} \leq 100$ in kPa
$1.1 \leq M_c \leq 1.55$
$0.7 \leq M_e \leq 1.25$
$0.005 \leq \lambda_c \leq 0.25$
$0.6 \leq e_0 \leq 1.8$
$0.2 \leq \xi \leq 1.0$
$50 \leq G_0 \leq 200$ in kPa
$0.001 \leq \nu \leq 0.1$
$0.005 \leq m \leq 0.05$
$0.6 \leq n_b \leq 2.5$
$1.0 \leq h_0 \leq 10.0$
$0.3 \leq c_h \leq 1.1$
$0.5 \leq n_d \leq 4.0$
$0.2 \leq A_0 \leq 1.4$
$1 \leq z_{max} \leq 60$
$50 \leq c_z \leq 10,000$

If you want to modify the bounds, e.g. to fine tune some parameters for the performance in cyclic tests, you can modify all of the above using the set_bounds function of the sanisand2 class:

...
# parameter from previous calibration
G0 = 126.03231709791712 
nue = 0.05 
h0 = 3.55966109923681 
# modify the bounds of G0 and m to be near the value from monotonic tests
model.set_bounds(G0=(0.25*G0,2.5*G0), m=(0.8*m,1.2*m), h0=(0.8*h0,1.2*h0))
...

Constraints

If either $M_c$ or $M_e$ or both are active during optimization, we enforce $M_e \leq M_c$ using a simple penalty approach.

Usage

To access the SANISAND constitutive model for optimization, the sanisand2 module must first be imported from numgeo-ACT:

from ACT.sanisand2 import sanisand2

Then (after some more steps to read in the experimental data and choose the constitutive model and the weighting factors) the sanisand2 class can be initialized:

model = sanisand2()

In a next step we initialize some of the parameters of the SANISAND model:

model.set(p_atm = 100, e0 = 1.0, phic = 32, c_z = 2400, z_max = 100)

We initialize $p_{atm}=100$ kPa and $\varphi_{c}$ as the angle of repose obtained from laboratory tests, respectively. Since for the sake of this example we are only interested in the calibration of “monotonic” parameters, we as well initialize $c_z$ and $z_{max}$ to - in this case - known values form a complete calibration performed in the past.

By initializing $\varphi_c$ instead of $M_e$ and $M_c$, the slopes of the CSL in triaxial compression and triaxial extension are automatically initialized as $M_c = 6\sin(\varphi_c)/(3-\sin(\varphi_c))$ and $M_e = 6\sin(\varphi_c)/(3+\sin(\varphi_c))$. Of course $M_c$ and $M_e$ could have also been initialized (without obeying above equations for $M_c(\varphi_c)$ and $M_e(\varphi_c)$) instead of $\varphi_c$.

In the last step we specify which parameters we want to vary during optimization. In the present case we want to optimize all parameters of the SANISAND model influencing the models response during monotonic loading. For convenience, the reference pressure $p_{atm}$ is kept constant.

to_optimize = \['e0','lambda_c', 'xi', 'M_c', 'M_e', 'm', 'G0', 'nue', 'h0', 'c_h', 'n_b', 'A0', 'n_d'\]

We have now successfully set up the SANISAND constitutive model for optimization by one of the implemented optimization algorithms $\rightarrow$ Optimization algorithms

Estimation of $e_0$, $\phi_c$ and $\lambda_c$ from undrained monotonic triaxial tests

In addition to a rigorous heuristic determination of the parameters $e_0$, $\phi_c$ and $\lambda_c$, we additionally provide a simple (and fast) determination of these parameters based on results of triaxial compression tests. The results can either be used as a starting (initial) value for the heuristic optimization or kept constant during the optimization.

model.estimate_e0_lambda_xi(triax_CU=excel.triax_CU)

where triax_CU requires a list of experimental results of undrained triaxial tests stored in the class triax_CU. The result of this function call is printed in the file e_p_lambdac.pdf in the results directory. An example is given in the following:

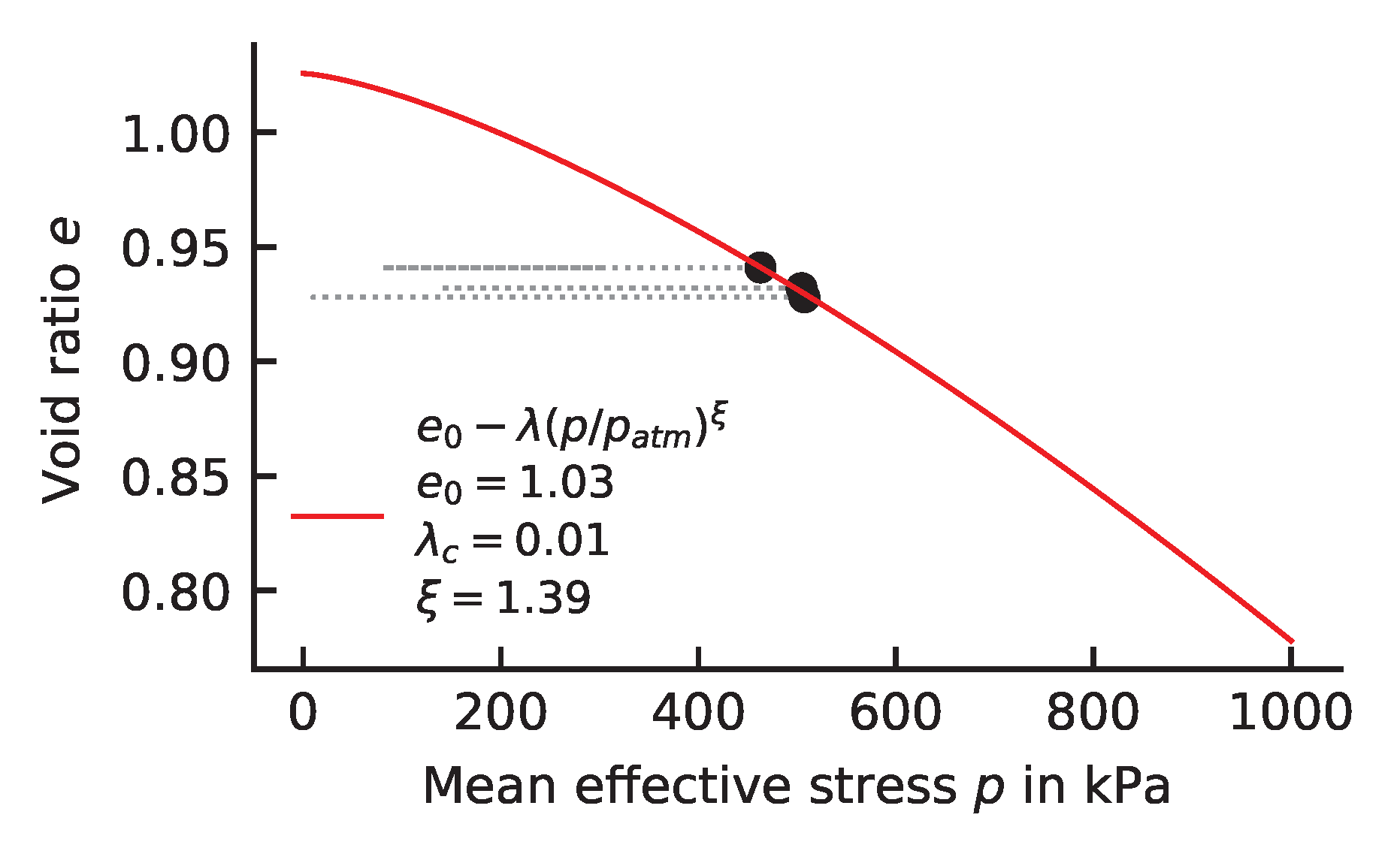
e_p_lambdac

Constitutive Equations

SANISAND [1] is an elasto-plastic model of the following form:

\[\dot{\boldsymbol{\sigma}} = \sf{E^{ep}} :\dot{\boldsymbol{\varepsilon}}\]

with total strain rate $\dot{\boldsymbol{\varepsilon}}$ and the elasto-plastic stiffness $\sf E^{ep}$:

\[\sf E^{ep} = 2G(\textbf{I}-\vec{\boldsymbol{1}}\vec{\boldsymbol{1}}) + K \vec{\boldsymbol{1}}\vec{\boldsymbol{1}} -\langle L\rangle\dot{\boldsymbol{\varepsilon}}^{-1} \big(2G\big[B\textbf{n}-C(\textbf{n}^2 - \frac{1}{3}\boldsymbol{1})\big] + KD \boldsymbol{1}\big)\]

The scalar elastic stiffness parameters $G$ and $K$ are defined as

\[\begin{aligned} G&=G_{0}~p_{atm}\frac{(2.97-e)^2}{1+e}\sqrt{\frac{p}{p_{\text{atm}}}}\\ K&=\frac{2(1+\nu)}{3(1-2\nu)}G. \end{aligned}\]

where $G_{0}$, $p_{atm}$ and $\nu$ are material parameters. The plastic multiplier (or loading index) $L$ is larger than zero if the yield surface representing a wedge in the 2D stress space and defined by

\[f=\sqrt{(\boldsymbol{\sigma}^{*}-p\boldsymbol{\alpha}):(\boldsymbol{\sigma}^{*}-p\boldsymbol{\alpha})}-\sqrt{\frac{2}{3}}pm <0\]

is no longer satisfied. The back-stress tensor $\boldsymbol{\alpha}$ defines the centre of the wedge and $m$ is the opening of the wedge. For stress states inside of the wedge, a hypoelastic material response is assumed.

\[\textbf{n} = \frac{\boldsymbol{\sigma}^{*}/p - \boldsymbol{\alpha}}{\sqrt{2/3}pm}\]

The plastic multiplicator $L$ is given by

\[L = \dfrac{2G \textbf{n}:\dot{\boldsymbol{\varepsilon}}^* - K \textbf{n}:\textbf{r}~ \text{tr}(\dot{\boldsymbol{\varepsilon}})} { K_p 2G (B -C \text{tr}~\textbf{n}^3) - KD \textbf{n}:\textbf{r}}.\]

$K_p$ is a hardening variable and defined as

\[K_p=\frac{2}{3}ph(\boldsymbol{\alpha}^b_{\theta} - \boldsymbol{\alpha}):\textbf{n}\]

where $h$ is given by

\[h=\dfrac{G_{0}h_{0}(1-c_{h}e)}{\sqrt{p/p_{\text{atm}}} (\boldsymbol{\alpha}-\boldsymbol{\alpha}_{\text{ini}}):\textbf{n}}\]

and $\boldsymbol{\alpha}^b_{\theta}$ by

\[\boldsymbol{\alpha}^b_{\theta}=\sqrt{\frac{2}{3}}\bigg[g(\theta,c)M\text{exp}(-n^b\psi)-m\bigg]\textbf{n}.\]

The update of the initial back-stress is performed in case of a load reversal which is detected according to one of the following conditions (depending on the method update_alpha specified in Optional parameters):

\[\boldsymbol{\alpha}_{\text{ini}}=\boldsymbol{\alpha} ~~~ if ~~~ \begin{cases} (1)&~~~ (\boldsymbol{\alpha}-\boldsymbol{\alpha}_{\text{ini}}):\boldsymbol{n} < 0 \\ (2)&~~~ (\boldsymbol{\alpha}-\boldsymbol{\alpha}_{\text{ini}}):\Delta \boldsymbol{T}^{el} < 0 \\ (3)&~~~ (\boldsymbol{\alpha}-\boldsymbol{\alpha}_{\text{ini}}): [\boldsymbol{T}-\text{tr}(\boldsymbol{T})/3 (\boldsymbol{\delta}+\boldsymbol{\alpha})] < 0 \end{cases}\]

$M$ is the stress ratio in the critical state, $n^b$ and $m$ are parameters introduced later. $\psi$ is the Been & Jefferies [2] state variable and defined as

\[\psi = e - e_c= e-e_{0}+\lambda_{c}~(p_c/p_{\text{atm}})^{\xi},\]

with the Lode angle function $g(\theta,c)$:

\[g(\theta,c) = \frac{2c}{(1+c)-(1-c)\cos(3\theta)} ~~~;~~~ \text{where}: ~\cos (3\theta) = \sqrt{6}\text{tr}(\textbf{n}^3).\]

The dilatancy $D$ is defined by:

\[D = A_d(\boldsymbol{\alpha}^d_{\theta} - \boldsymbol{\alpha}):\textbf{n}\]

where $\boldsymbol{\alpha}^d_{\theta}$ is

\[\boldsymbol{\alpha}^d_{\theta}=\sqrt{\frac{2}{3}}\bigg[g(\theta,c)M \text{exp}(n^d\psi)-m\bigg]\textbf{n}\]

and $A_d$

\[A_{d}=A_{0}(1+\langle \textbf{z}:\textbf{n}\rangle).\]

The change of the fabric-dilatancy tensor $\textbf{z}$ is

\[\dot{\textbf{z}}= -c_z\langle -d\varepsilon_{v}^{p}\rangle (z_{\text{max}}\textbf{n}+\textbf{z}).\]

Lastly, the change of the back-stress tensor $\boldsymbol{\alpha}$ is

\[\dot{\boldsymbol{\alpha}}= \frac{2}{3}\langle L\rangle h (\boldsymbol{\alpha}^b_{\theta} - \boldsymbol{\alpha})\]

References

[1] Y. F. Dafalias and M. T. Manzari, ‘Simple plasticity sand model accounting for fabric change effects’, Journal of Engineering mechanics, vol. 130, no. 6, pp. 622–634, 2004.

[2] K. Been and M. G. Jefferies, ‘A state parameter for sands’, Géotechnique, vol. 35, no. 2, pp. 99–112, Jun. 1985, doi: 10.1680/geot.1985.35.2.99.