Oedometric Compression Test
Table of contents
Finite Element (FE) representation
For the simulation of oedometric compression tests we perform a so-called ‘‘single-element-simulation’’ with the FE program numgeo and by doing so enforce element test assumptions, i.e. a homogeneous distribution of stress/strain within the test sample. A schematic of the FE representation of the oedometric compression test is given below.
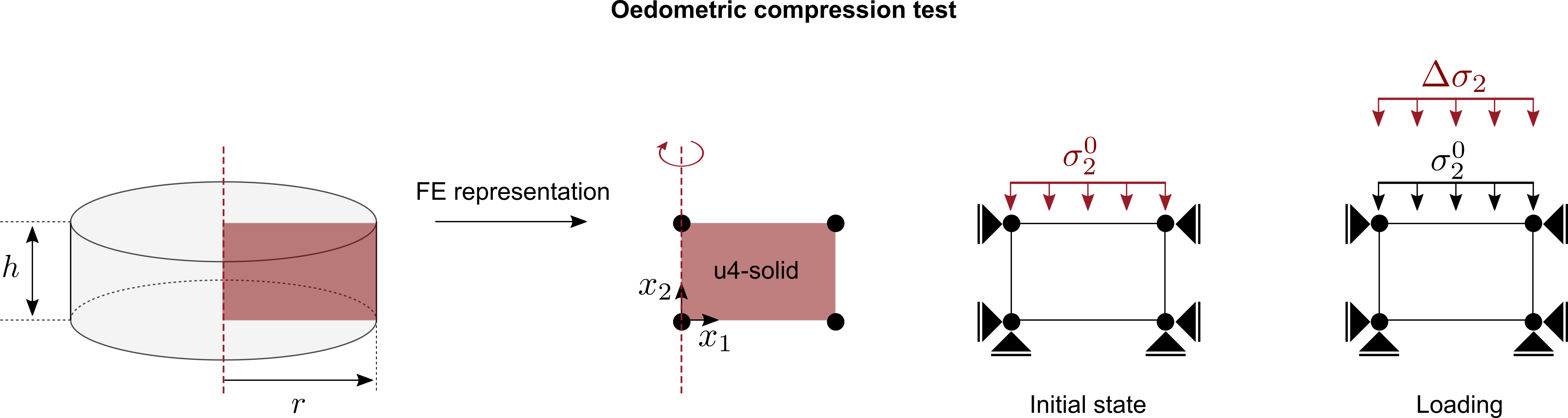
- An axisymmetric solid element with four nodes and linear shape functions for the displacement field is used
- In a first initial step, the initial conditions are applied, i.e. initial stress ($\sigma_2^0$ and, assuming $K_0=1$, $\sigma_1^0 = \sigma_2^0$), initial void ratio $e_0$ or any other initial state variable required by the constitutive model to be calibrated.
- In the second loading step, the loading is applied by prescribing an additional vertikal stress $\Delta \sigma_2$ on the top surface of the element. $\Delta \sigma_2$ is increased linearly starting from $\Delta \sigma_2=0$ until $\Delta \sigma_2^{max}$ is reached.
Sample numgeo input file
An example input file for the simulation of an oedometric compression test using Hypoplasticity with numgeo is shown below.
**=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=
** numgeo-ACT
** Copyright (C) 2022 Jan Machacek
**=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=
*Node
1 , 0.0 , 0.00
2 , 0.05, 0.00
3 , 0.05, 0.018
4 , 0.00, 0.018
*Nset, Nset=nall
1 , 2 , 3 , 4
*Nset, Nset=nleft
1 , 4
*Nset, Nset=nright
2 , 3
*Nset, Nset=nbottom
1 , 2
*Nset, Nset=ntop
3 , 4
*Element, Type=U4-solid-ax
1 , 1 , 2 , 3 , 4
*Elset, Elset = eall
1
** ----------------------------------------
*Solid Section, Elset = eall, material=soil
** ----------------------------------------
*Material, name = soil, phases = 1
*Mechanical = Hypoplasticity
0.561,0.0,27771046.0,0.19,0.621,1.123,1.15,0.254
2.483,1.0,1.0,0.0001,0.2,2.0, 0.0
*Density
2.65
** ----------------------------------------
*Initial conditions, Type = stress, geostatic
eall, 0.0, -1.548, 0.1, -1.548, 0.46778501154445673, 0.46778501154445673
*Initial conditions, Type = state variables
eall, void_ratio, 0.98968
eall, int_strain22, -0.0001
** ----------------------------------------
*Amplitude, name = LoadingRamp, Type=ramp
0.0, 0.0, 1.0, 1.0
** ----------------------------------------
*Step, name = Geostatic, inc=1
*Geostatic
*Body force, instant
eall, grav, 0.0, 0., -1, 0.
*Dload, instant
eall, p3, -1.548
*Boundary
nleft, u1, 0.
nright, u1, 0.
nbottom, u2, 0.
*Output, print
*Element output, Elset = eall
S, E, void_ratio
*End Step
** ----------------------------------------
*Step, name = Loading, inc = 100000, maxiter = 16
*Static
0.00001, 1., 0.00001, 0.01
*Body force, instant
eall, grav, 0.0, 0., -1, 0.
*Dload, instant
eall, p3, -1.548
*Dload, amplitude = LoadingRamp
eall, p3, -405.541
*Boundary
nleft, u1, 0.
nright, u1, 0.
nbottom, u2, 0.
*Output, print
*Element output, Elset = eall
S, E, void_ratio
*End Step
** ----------------------------------------
*End Input