Undrained monotonic triaxial test
Development of geometry model
The initial step to set up a problem in numgeo with GiD is creating a geometry. For this, use the straight line 
or enter exact coordinates into the command line.
The following coordinates are used for the undrained monotonic triaxial test.
0.0, 0.0
1.0, 0.0
1.0, 1.0
0.0, 1.0
Mesh generation
A quadrilateral mesh element is defined in this test, since it is a quadratic geometry and only one mesh element is needed. Create the mesh by entering the element size of 1.0 m. For a better overview toggle the mesh-view using the button 
on the left bar. Speed up the mesh creation using 'CTRL+G'.
Input definition
To add properties to the input file, the numgeo problem type 
must be loaded in GiD (Data -> Problem type -> numgeo). A data tree will then be shown on the left side.
The relevant groups can be added either before or while getting through the data tree. The groups will be shown on the tab on the right side. For the groups nleft, nright, ntop and nbottom select each line. For the group eall the complete surface needs to be elected.
Now, use the data tree in the left to navigate through the settings and proceed in the order in which they are listed.
- First, choose the right problem dimension
(2D: Axisymmetric) and assign an element type 
(single-phase solid) for all elements. - Define the material name 'soil', the number of phases and the density of the material. Next, choose the material model under Stress-Strain
and define the listed material parameters. Then assign the material 
to all elements.
For the undrained monotonic triaxial test the material parameters of Hypoplasticity + Intergranular Strain Anisotropy are defined as follows:
| parameters | value | parameters | value | |
|---|---|---|---|---|
| \( φ \) | 0.578 rad | \( β_{h0} \) | 0.07 | |
| \( h_s \) | 9958000 kN/m² | \( χ^0 \) | 10.149 | |
| \( n \) | 0.252 | \( χ^{max} \) | 10.832 | |
| \( e_{d0} \) | 0.643 | \( ϵ^{acc} \) | 0.017 | |
| \( e_{c0} \) | 1.066 | \( c^{z} \) | 762.0 | |
| \( e_{i0} \) | 1.119 | \( β_{hmax} \) | 2.078 | |
| \( α \) | 0.155 | \( E_{ph} \) | 50.0 | |
| \( β \) | 2.906 | \( ν_{ph} \) | 0.450 | |
| \( m_R \) | 1.345 | \( p_{min,ph} \) | 1.0 | |
| \( R \) | 0.000179 | \( K^{ω} \) | 0.0 0.0 kN/m² |
- Next, we define the amplitude
as a ramp and change the name to 'LoadingRamp'. The default values are correct for the undrained monotonic triaxial test. - The initial stress
and some state variables 
must be applied for this element test to all elements. For the state variables, the name of every variable must be typed in with the corresponding value.
Initial stress:
- option:
geostatic- \( z_1 \):
0.0- \( σ_1 \):
-402.7- \( z_2 \):
0.1- \( σ_2 \):
-402.7- \( k_{0,x} \):
0.994- \( k_{0,y} \):
0.994State variables:
- void_ratio:
0.819- int_strain11:
-0.0001035- int_strain22:
-0.0001035- int_strain33:
-0.0001035- int_back_strain11:
-5.18e-05- int_back_strain22:
-5.18e-05- int_back_strain33:
-5.18e-05
Step 1: 
Static
- Finally, the step can be defined. For this, change the name of the step to 'Static' and enter the number of increments of 10000.
- Change the analysis type
to static. Now the input of time integration 
is unlocked. The following values for time integration are used:
- Initial time step:
0.001 s- Time step (total):
1 s- Minimum time step:
0.001 s- Maximum time step:
0.001 s
- Below the tab '
Dirichlet boundary conditions’ the solid displacements in both directions can be defined. Fix the displacements in the x-direction of nleft and in the y-direction for nbottom. - In addition, the linear increasing vertical displacement of the top nodes is prescribed to -0.05. Similiar to that, the linear increasing hotizontal displacement of the right nodes is prescribed to 0.025. Note: Select LoadingRamp for the amplitude, as this is a non-constant displacement.
- Apply the gravity force to all elements. The default values are already given there. In addition to the gravity force, define a pressure of -402.7 kN/m² on the top and a pressure of -400.3 kN/m² on the right side, both with an instant loading rate.
- Since this is a basic simulation, only print output
for all elements is requested for stress, strain, and void ratio.
Results and visualization
Save the file in a folder, where the problem should run and start the calculation process (numgeo -> Generate numgeo files). numgeo will automatically create two input files and start calculating. Once the calculation process is finished, the results can be plotted using python for example.
The following Python script was used to plot the data shown in figure 1.
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
plt.rcParams['text.usetex'] = True
plt.rcParams['font.size'] = 12
plt.rcParams['axes.spines.right'] = False
plt.rcParams['axes.spines.top'] = False
def cm2inch(*tupl):
inch = 2.54
if isinstance(tupl[0], tuple):
return tuple(i/inch for i in tupl[0])
else:
return tuple(i/inch for i in tupl)
sim = np.genfromtxt('./undr-mono-print-out/EALL_element_1.dat', skip_header=1)
fig, (ax1,ax2) = plt.subplots(ncols=2, sharey=True, figsize=cm2inch(16,8))
ax1.plot(-sim[:,8]*100, -(sim[:,2]-sim[:,1]), label='Simulation', color='purple')
ax1.set_ylabel('Deviatoric stress $q$ in kPa')
ax1.set_xlabel('Axial strain $\\varepsilon_{ax}$ in \%')
ax1.legend(loc='lower right', frameon=False)
ax2.plot(-(sim[:,1]+sim[:,2]+sim[:,3])/3., -(sim[:,2]-sim[:,1]), label='Simulation', color='purple')
ax2.set_xlabel('Mean effective stress $p^\prime$ in kPa')
fig.tight_layout()
plt.savefig("stress-strain",dpi = 900)
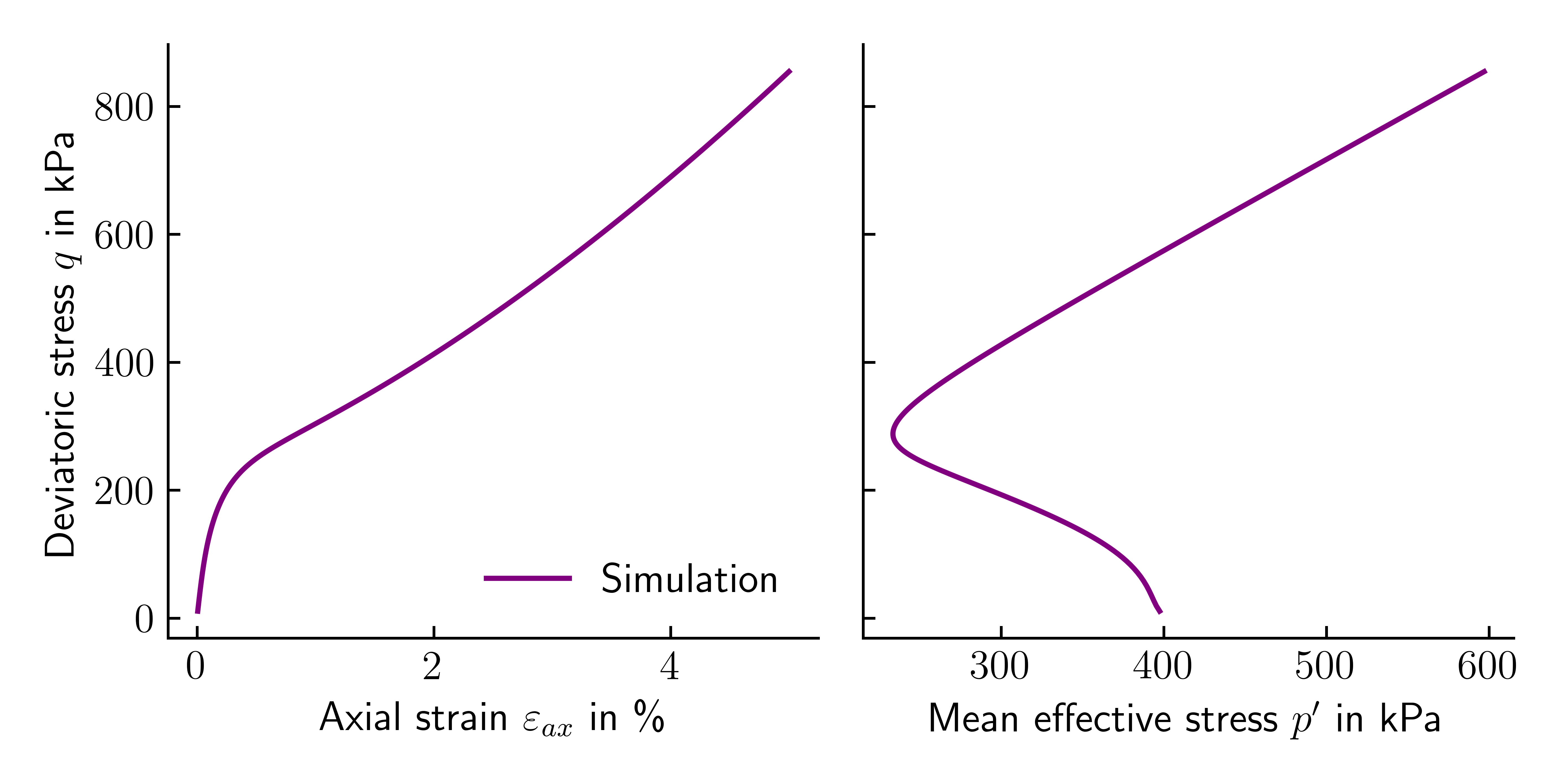
For more information please refer to the corresponding numgeo tutorial for the Undrained monotonic triaxial test.