Observations (Sand)
In the previous section on Triaxial Test, we delved into the setup and execution of monotonic triaxial tests. Our focus was on how various factors - namely the initial mean effective pressure (\(p^\prime\)), the initial relative density (\(D_{r0}\)), and the drainage conditions - influence the stress-strain behaviour of sand. The main observations were:
- Increasing the initial mean effective pressure (\(p^\prime\)) leads to an increase in the sand's shear strength.
- A higher initial relative density (\(D_{r0}\)) correlates with increased shear strength.
- Dense sand samples exhibit higher peak shear strengths compared to loose samples at the same \(p^\prime\). However, as shear strain increases, the shear strength of dense samples decreases, eventually aligning with that of loose samples.
When comparing tests on sand with identical \(D_{r0}\) and \(p^\prime\) but varying drainage conditions (refer to undrained triaxial compression tests and undrained triaxial extension tests), a fundamental difference in stress-strain behaviour emerges, dependent on the drainage condition. Yet, at high shear strains, the stress state in the \(p^\prime-q\) plane can be approximated by a single line, characterized by slopes \(M_c\) for triaxial compression and \(M_e\) for triaxial extension.
This brings us to an essential question: Are these observations consistent across a broad range of relative densities and mean effective pressures? Can we replicate these findings, and do they provide a reliable foundation for a framework (model) to describe the behaviour of soils, both cohesive and non-cohesive, under varying (loading) conditions? To edge closer to these answers, we'll examine the comprehensive experimental data on Karlsruhe fine sand from 1. Our exploration will be structured in subsections, starting with drained and undrained conditions separately and then considering both in conjunction.
Drained monotonic triaxial tests
The results of 25 drained triaxial compression tests on Karlsruhe Finesand for different initial relative densities \(D_{r0}\) and initial mean effective pressures \(p^\prime\) are summarized in the following animation. The results of these tests are reported by means of deviatoric stress over axial strain (\(\varepsilon_1-q\)), deviatoric stress and void ratio over mean effective pressure (\(p^\prime-q\) and \(p^\prime-e\)). All samples were created by air pluviation of dry sand and subsequent saturation of the soil sample. The initial densities span from 0.15 to 0.95.
Test results of 25 drained monotonic triaxial tests on Karlsruhe Finesand. The solid dots represent the initial conditions and the hollow points the final state of the experiments. (click to play)
Undrained monotonic triaxial tests
In addition to the drained triaxial tests, more than 100 undrained triaxial compression tests were performed. However, the complete experimental data is available only for a limited number of these tests. In the following animation, the test results of 9 undrained triaxial compression tests are depicted. The tests are performed on samples of different initial relative densities and at different initial effective pressures.
Test results of 9 undrained monotonic triaxial tests on samples of Karlsruhe Finesand created by air pluviation. The solid dots represent the initial conditions and the hollow points the final state of the experiments. (click to play)
The relative densities in these tests ranged from 0.28 to 0.82. Very low relative densities, e.g. below 20%, can hardly be achieved using the air pluviation technique. In order to reach even lower initial densities, many of the undrained triaxial tests have been prepared by moist tamping. Again, these tests were performed on samples with different initial relative densities in the range of \(0.04 \leq D_{r0} \leq 0.4\). The results of 9 of these tests are shown in the animation below.
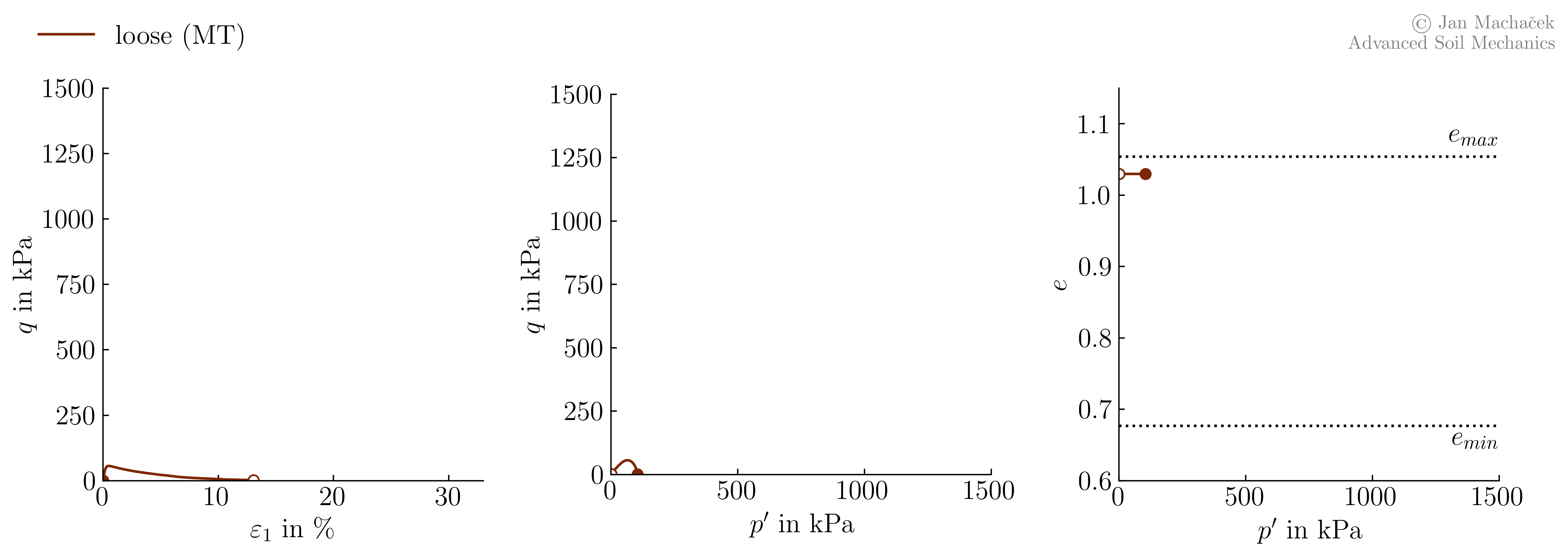Test results of 9 undrained monotonic triaxial tests on samples of Karlsruhe Finesand created by moist tamping. The solid dots represent the initial conditions and the hollow points the final state of the experiments. (click to play)
Observation 1
Comparing the results of the undrained triaxial compression tests on samples created by air pluviation and by moist tamping it becomes obvious that the sample preparation method influences the stress-strain behaviour significantly, especially in the early stages of the experiments at small to medium strains.
The reason for this is the inherent fabric generated during the sample preparation process, i.e. the grain skeleton has a different structure for samples obtained by air pluviation and by moist tamping. Very loose samples (prepared by moist tamping) tend to show contractive behaviour leading to full liquefaction (\(p^\prime=0\)). In contrast, denser samples show slight contraction initially, followed by dilatancy at larger strains. However, it can also be observed that at very large shear strains, the behaviour of sand does not depend so much on the initial fabric, because this fabric is presumably erased at large shear strains.
Combining the data
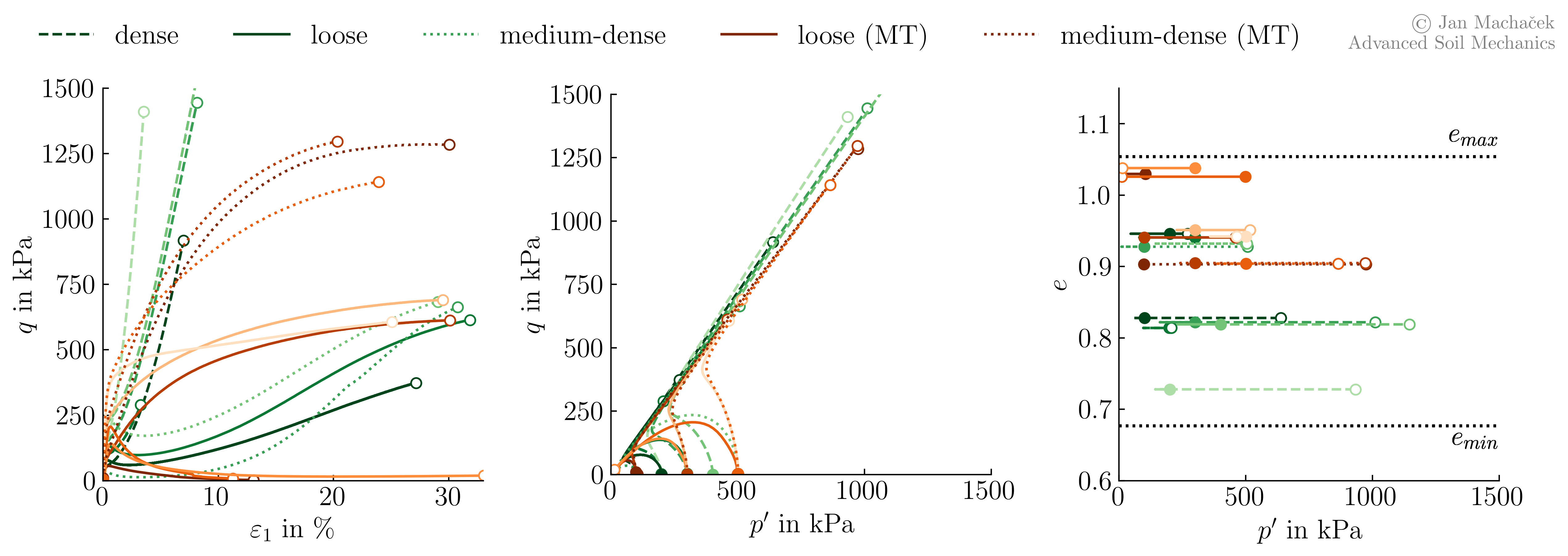
To spot similarities in soil behaviour for different drainage conditions, we combine all test results in one common plot. Different colors represent different tests: blue are the drained triaxial compression tests on samples created by air pluviation (CD AP), green are the undrained triaxial compression tests on samples created by air pluviation (CU AP) and orange are the undrained tests on samples created by moist tamping (CU MT).
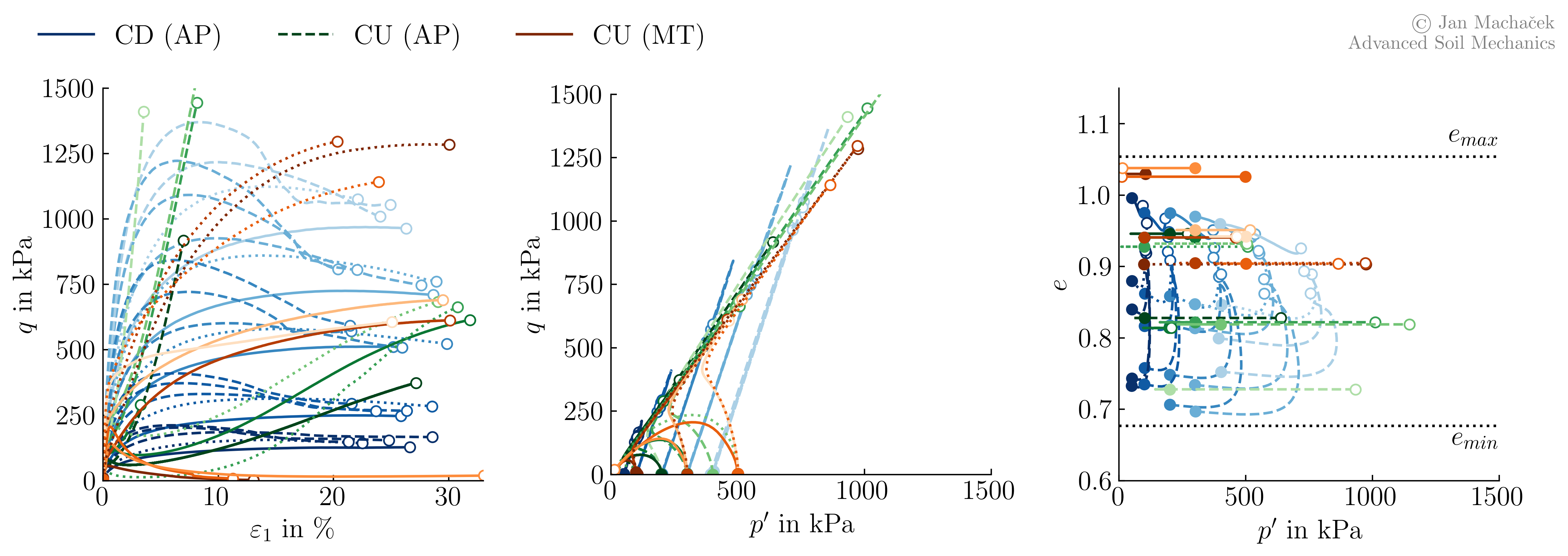Test results of 25 drained and 18 undrained monotonic triaxial tests on samples of Karlsruhe Finesand. The solid dots represent the initial conditions and the hollow points the final state of the experiments.
From these results we can observe that, independent from the initial conditions (\(p^\prime\), \(D_{r0}\), sample preparation), at large strains the stress paths (\(p^\prime-q\)) of all samples are similar and seem to converge to (or near) common line, usually referred to as the failure line. In order to make this better visible, we reduce above plot to only show the final stage of all experiments in \(p^\prime-q\) and in \(p^\prime-e\) space.
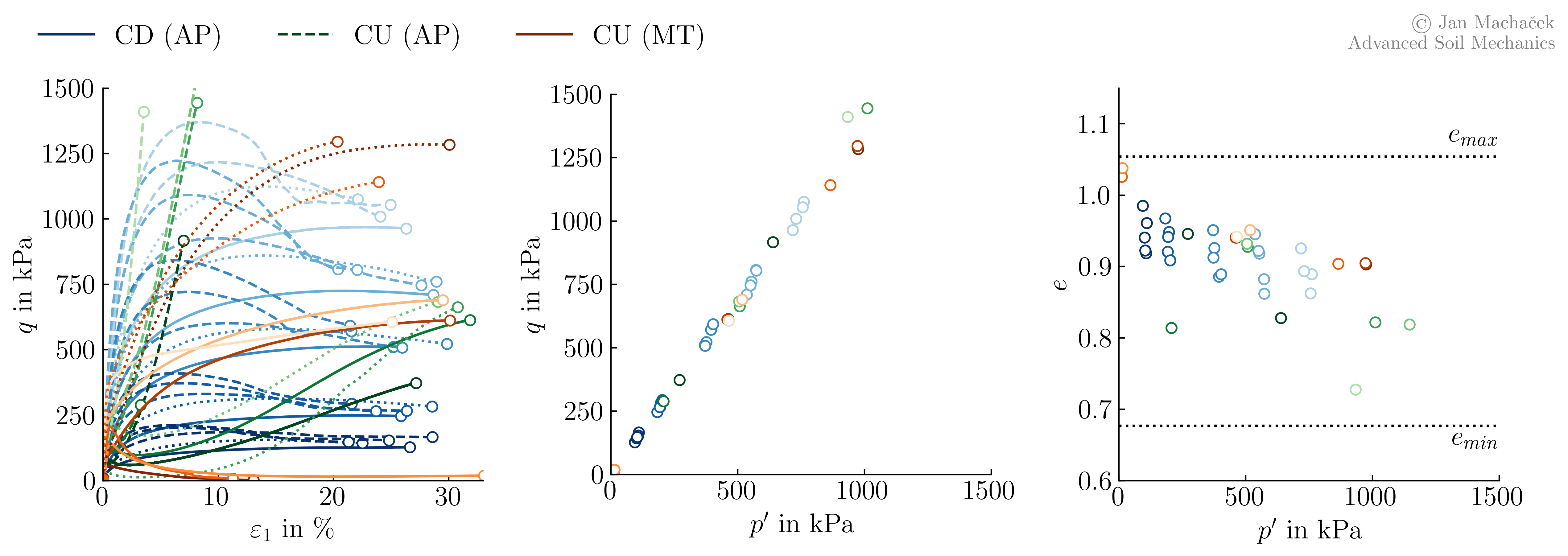
Observation 2
Regardless of the drainage conditions (undrained or drained), initial conditions (mean effective pressure \(p^\prime\) and initial density \(D_{r0}\)) or the sample preparation method (air pluviation or moist tamping) stress paths in \(p^\prime-q\) space of Karlsruhe Finesand converge to a common line at large strains, known as the failure line.
Compared to the observed behaviour in the \(p^\prime-q\) plane, such a unique relation is not as clearly visible in the \(p^\prime-e\) plane, where larger scatter of the final state in terms of void ratio is apparent. The reason for this lies in the high sensitivity of the void ratio to sample inhomogeneities, i.e. the formation of shear bands. Especially for triaxial tests on dense samples the formation of shear bands (see below and Section Concluding comparison) is inevitable.
After the formation of a shear band, dilatancy only happens within a narrow range of deformation inside the shear band. It is compensated for by a slight compression in the remaining volume of the specimen, so that the total volume of the specimen remains unchanged. For this reason the post-peak behaviour of drained monotonic triaxial tests on dense samples is often considered not "trustworthy" and if too excessive sample deformations are observed in the experiments they are stopped. Since we are interested in the behaviour at large strains anyway, these tests can simply be filtered out by considering a threshold shear strain. As a rule, a minimum strain of \(\varepsilon_1=25\) % is required. If this is taken into account when analysing the data, the following picture emerges:
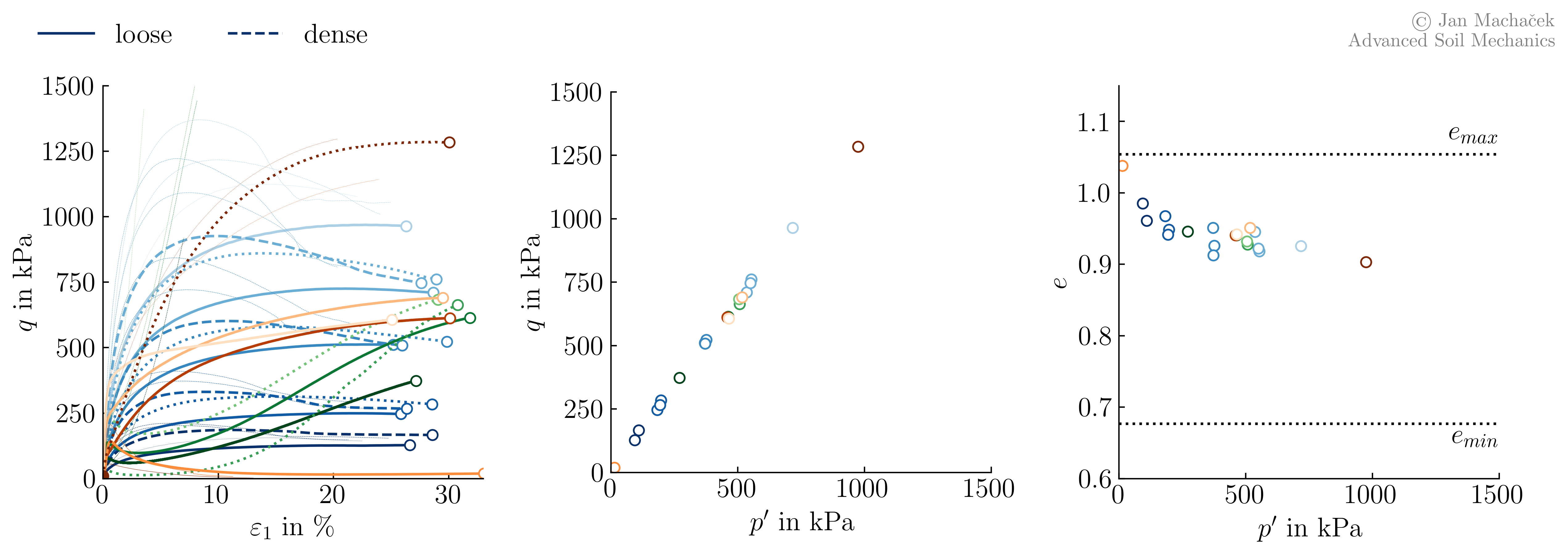
From the figure above, a logarithmic relationship between the void ratio \(e\) and the mean effective pressure \(p^\prime\) can be anticipated. For further consideration, a corresponding representation of \(e\) via the logarithm of the mean effective pressure is therefore used.
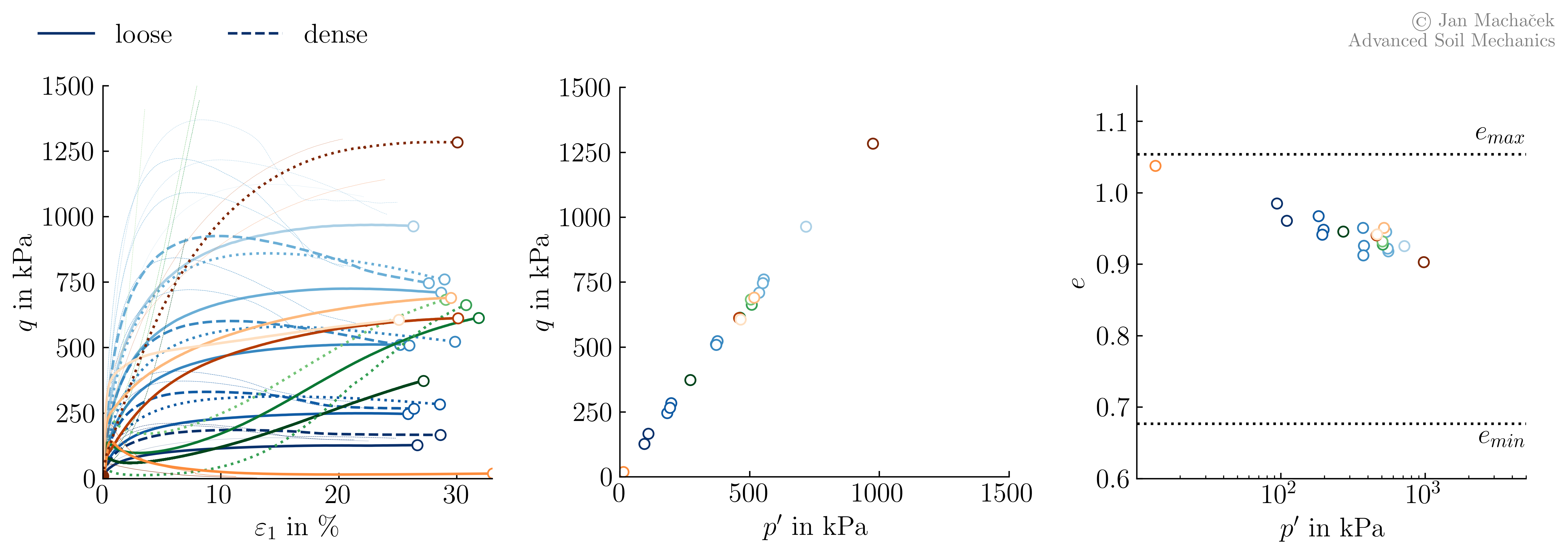
As stated at the beginning of this chapter, more than 100 undrained monotonic triaxial tests have been performed in the study reported in 1. Although the complete data is only available for a subset of these tests, the final void ratios for undrained monotonic compression tests evaluated at \(\varepsilon_1=25\) % are available as well. Adding these to the already discussed data, we obtain the following:
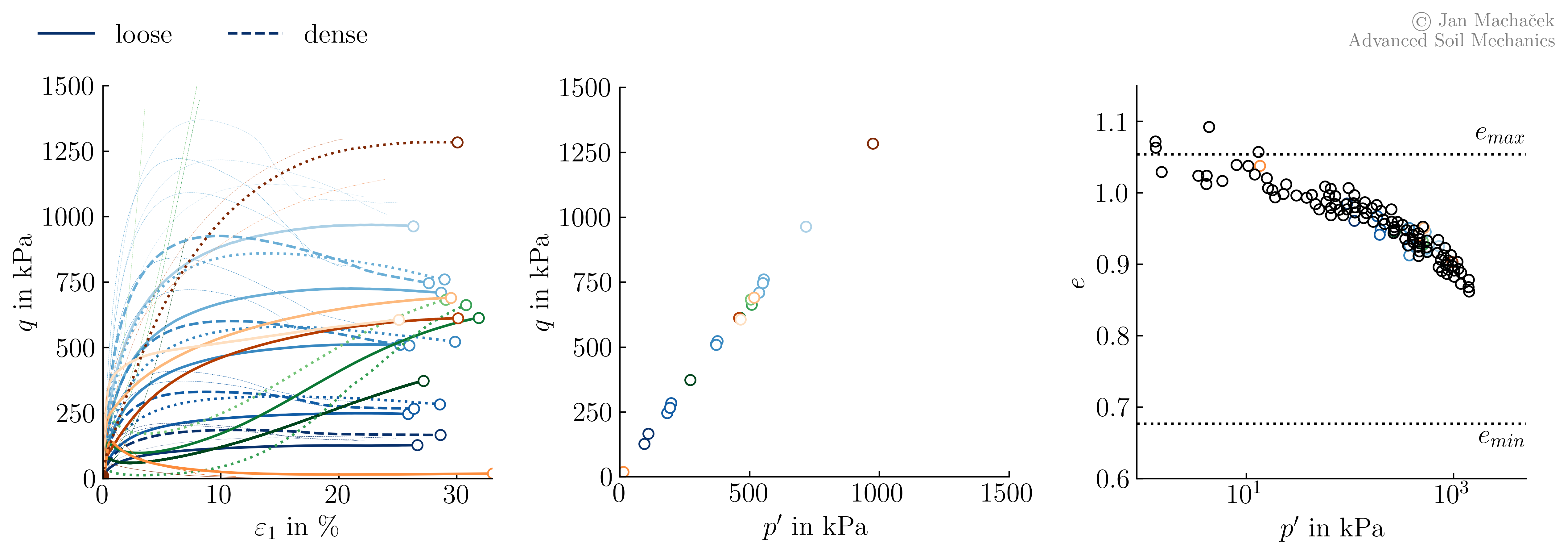
What was previously only a "suspicion" of a unique relationship between the void ratio and the mean effective pressure at the critical state is now confirmed by the entirety of the data leading to the third observation:
Observation 3
When considering a minimum strain of 25%, we observe a logarithmic relationship between void ratio (\(e\)) and mean effective pressure (\(p^\prime\)). This relationship holds true across all tests, confirming a unique correlation at the critical state.
-
T. Wichtmann and T. Triantafyllidis, ‘An experimental database for the development, calibration and verification of constitutive models for sand with focus to cyclic loading: part I—tests with monotonic loading and stress cycles’, Acta Geotech., vol. 11, no. 4, pp. 739–761, Aug. 2016, doi: 10.1007/s11440-015-0402-z. ↩↩