Numerical Integration

To solve the discretised integral over the weighted residual

\[ R_I(u^*(x),x) = \approx \sum_{Ie}^{Ne} \int_{\Omega_e} N_I(x) D(u^*(x),x) d \Omega_e ~~~\text{with:}~ I = \{1,2,...N\}, \]

the individual terms must be integrated over the volume $\Omega_e$ of each element. The evaluation of these integrals is however difficult and their analytical solution if often impossible. This is mainly due to the fact that the coefficients of the integrals, e.g. stiffness or the permeability, are often complicated functions of position $\mathbf{x}$, i.e. they may vary greatly across space. Consequently, numerical integration is used instead of exact integration. The numerical method used here is the Newton-Cotes approach. The idea of this approach is to approximate the integral of a given function $f(x)$ by a suitable polynomial function $P(x)$ and to integrate this exactly. In the context of the FEM, so-called Lagrange basis functions $L_I(x)$ are often used to build $P(x)$. These have the property that they are exactly 1 at the considered grid point and 0 at all other grid points. If we want to write it down formally for a 1D function, we get:

\[ \begin{equation}\label{eq:numerical-integration-1} \int_a^b f(x) d x \approx \int_a^b P(x) d x = \sum_{I=1}^N f(x_I) \int_a^b L_I(x) dx \end{equation} \]

Note on Equation ($\ref{eq:numerical-integration-1}$)

If there is a sum within an integral, then this is equivalent to the sum of the single integrals:

\[ \int_a^b \sum_{I=1}^N f(x_I)L_I(x) dx = \sum_{I=1}^N \int_a^b f(x_I)L_I(x) dx \]

Further, constants ($f(x_I)$ is the value of the function $f$ at the point $x_I$ and thus constant) may be subtracted from the integral:

\[ \sum_{I=1}^N \int_a^b f(x_I)L_I(x) dx = \sum_{I=1}^N f(x_I) \int_a^b L_I(x) dx \]

If we now take a closer look at this equation, we can see that the function to be integrated $f(x)$ is no longer inside the integral. Its value is only needed at single, discrete points $x_I$ - which we denote as "integration point". This in turn means that we can think in advance how to solve the integral $\int_a^b L_I(x) dx$, which makes the approximation of the integral of $f(x)$ easier. We only have to multiply the discrete values $f(x_I)$ with the numbers which come from the integral $\int_a^b L_I(x) dx$. A sketch illustrating this is given in Figure 1.

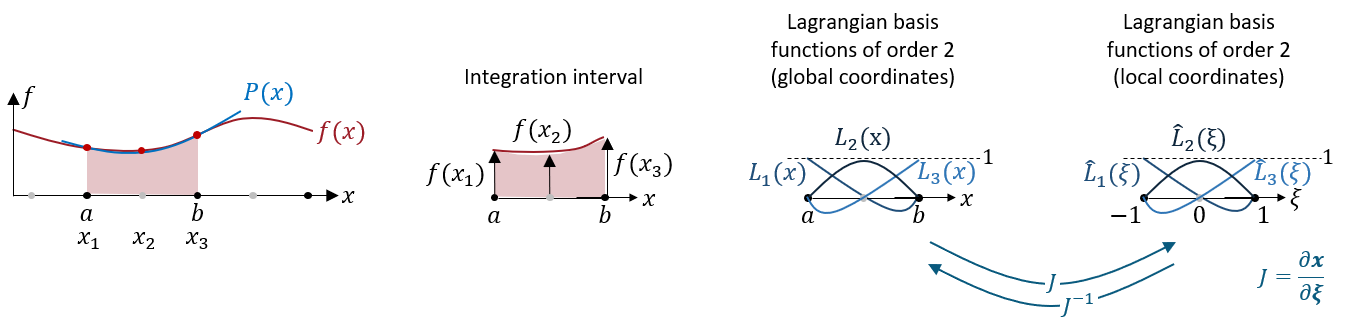
Figure 1. Simplified representation of the numerical integration with the Newton-Cotes approach and its components.

If we think back to the field of application - the FEM - it becomes obvious that the integration limits $a$ and $b$ are not constant, after all, the individual elements can have different dimensions. In order to be able to determine the integral nevertheless in the apron, still another step is necessary. The derivation of this step I will owe in the context of this script - but it can be read in the most important standard works. Anyway, the result of this step is that it is wise to formulate the Lagrangian basis functions $\hat{L}_I(\xi)$ in so-called natural (or local) coordinates $\xi$, which in most cases range from $-1$ to $1$ (or in the case of triangular elements from $0$ to $1$) - independent of the dimensions of the element in the physical (global) coordinate system. This requires, that the integration area (defined in the global or physical domain) is mapped in a local (or reference) domain with the local (natural) coordinate $\xi$. The mapping has to be bijective, as it has to provide also the inverse mapping from local coordinates $\xi$ to global coordinates $x$. This mapping is depicted for a 1D example under investigation in Figure 1 and exemplarily for a triangular finite element in Figure 2.

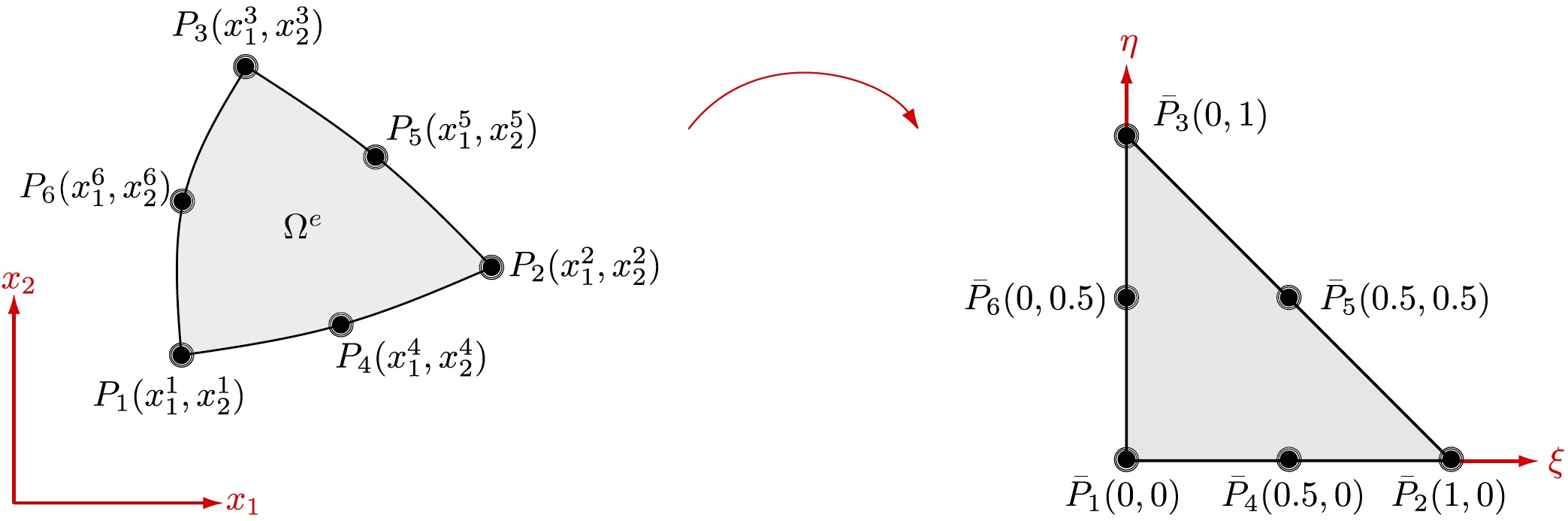
Figure 2. Triangular element with six nodes in current, global configuration (left) and in local (reference) configuration (right).

With this mapping of the element in the physical domain to the natural domain, the integration from Eq. \ref{eq:numerical-integration-1} for the 1D example from Figure 1 becomes:

\[ \begin{equation}\label{eq:numerical_integration_2} \int_a^b f(x) d x \approx \sum_{I=1}^N f(x_I) J \int_{-1}^1 \hat{L}_I(\xi) d\xi. \end{equation} \]

Therein, $J = \partial x/\partial \xi = (\partial \boldsymbol{\hat{L}}/\partial \xi) x$ is known as the Jacobian of the transformation / mapping $x \rightarrow \xi$. The integral $\int_{-1}^1 \hat{L}_I(x) d\xi$ now depends exclusively on the functions $\hat{L}$ (defined in natural coordinates) and the natural coordinates $\xi$. It can therefore be pre-calculated. And this is where the mathematician Gauss came into play: he found that there exists an optimal choice of interpolation points with which polynomials of degree $2N-1$ can be integrated exactly. The optimal position of the integration points depends on the element shape / functions $\hat{L}$. Equation ($\ref{eq:numerical_integration_2}$) reduces then to a simple summation:

\[ \begin{equation}\label{eq:numerical_integration_3} \int_a^b f(x) d x \approx \sum_{I=1}^N f(x_I) w_I J \end{equation} \]

In this $w_I$ is the so-called weighting factor - which is nothing else than the integral calculated at the integration point $I$ (with position $\xi_I$). For the example of the 2D triangular element depicted in Figure 2, the numerical integration reads:

\[ \begin{equation}\label{eq:numerical_integration_4} \int_{\Omega_e} f(x) d \Omega_e \approx \int_0^{-1} \int_0^{1-\xi} f\big(\mathbf{x}(\boldsymbol{\xi})\big) J d \eta ~ d \xi = \sum_{I=1}^{N} \sum_{J=1}^N w_I w_N f\big(x_1(\xi_I,\eta_J),x_2(\xi_I,\eta_J)\big) J(\xi_I,\eta_J) \end{equation} \]

Now that we have moved from a 1D system to a 2D system, the number of dimensions also increases. So the global and local positions are now defined by $\boldsymbol{x}=\{x_1,x_2\}$ and $\boldsymbol{\xi}=\{\xi,\eta\}$, respectively. The area of the element $d \Omega_e = J d \eta ~ d \xi$, where $J = \text{det}(\boldsymbol{J})$ now denotes the determinant of the Jacobian. Note that the positions of the integration points $\xi_I$ and their corresponding weights $w_I$ are constant and independent from the actual element dimension. They only depend on the element shape (e.g. triangular, rectangular,...) and the number of nodes of the element (e.g. tri-noded or six-noded triangular element). An example is given in Figure 3, where the location of the integration points as well as their corresponding weighting factors are depicted for a six-noded triangular shaped element with quadratic shape functions. The transfer to rectangular elements or three-dimensional elements is straight forward and is not shown in detail.

Figure 3. Location and weights of integration (Gauss) points for a six-noded triangular shaped element with quadratic shape functions.

The question now naturally arises as to what these functions $\hat{L}$ are. In the FEM they correspond exactly to the functions which are used for the approximation of the solution $\phi$ (and in the approach according to Galerkin also to the weighting functions $\psi$). Therefore, in the following we will only speak of the shape functions $N$. More precisely, we will speak of $N_I(\mathbf{x})$, i.e. the shape function $N$ which belongs to node $I$ and is evaluated at a point within the element with position $\mathbf{x}$. Each element type has - depending on its shape and the number of nodes - its "own" shape functions. A list of all functions would go too far at this point, so reference is made to corresponding standard works such as Belytschko (2014)¹ or Bathe (2014)². An example is given for triangular elements, one with 3 nodes (a so-called linear interpolated element) and one with 6 nodes (a so-called quadratic interpolated element).

Figure 4. Example of a triangular shaped element. Top: six-noded (quadratic) element, bottom row: three-noded (linear) element.

The shape functions depicted in Figure 4 are given in the following. For the six-noded triangular element biquadratic shape functions are used:

\[ \begin{equation} \begin{aligned} N_1 &= (1-\xi-\eta)(1-2\xi-2\eta) &,~~~~~ N_2 &= \xi(2\xi-1)&,~~~~~ N_3 &= \eta(2\eta-1) \\ N_4 &= 4 \xi (1-\xi-\eta) &,~~~~~ N_5 &= 4\xi\eta &,~~~~~ N_6 &= 4 \eta (1-\xi-\eta), \end{aligned} \end{equation} \]

whereas for the tri-noded triangular element bilinear shape functions are used:

\[ \begin{equation} N_1 = (1-\xi-\eta) ~~~,~~~~~ N^p = \xi ~~~,~~~~~ N_3 = \eta. \end{equation}\$$5 mm \]

Practical relevance

It is important to always keep in mind that FEM is a numerical method to solve partial differential equations (PDEs) approximately by reducing the continuous mathematical model to a discrete idealization. This is done by dividing the domain into a (finite) number of small elements with simple geometry on which the physical fields are approximated in a piece-wise manner. The primary solution of the PDE is sought at the nodes (i.e. the connection points of the individual elements) - in the context of geotechnical calculations, these are usually displacements or pore water pressures. Between the nodes, the distribution of the solution is assumed, following (comparably) simple approximation functions. Secondary solution variables, i.e. those that are required for the PDE but have not been discretised at the nodes, are calculated within the elements at fixed positions (so-called integration points). In geotechnics, these could be e.g. stresses, degree of saturation or pore water velocity. Although it has not been shown here, it is important to emphasize that the choice of approximation functions can have a significant impact on the solution, especially on the secondary solution variables. We will consider this in the following with a simple example.

Ted Belytschko, W. K. Liu, B. Moran, and Khalil I. Elkhodary. Nonlinear Finite Elements for Continua and Structures. Wiley, Chichester, West Sussex, United Kingdon, second edition edition, 2014. ISBN 978-1-118-63270-3. ↩
Klaus-Jürgen Bathe, editor. Finite Element Procedures. K.J. Bathe, Watertown, MA, 2nd edition edition, 2014. ISBN 978-0-9790049-5-7. ↩