Unsaturated soils
So far - in this course, but also in other courses in your curriculum - the concepts of soil mechanics have primarily navigated the extremes: soils in dry states or fully saturated conditions, whether drained or undrained. These scenarios, while fundamental, represent only the tip of the iceberg in our understanding of soil behavior.
Consider the natural world around you – the soil in your garden, the sand at the beach, or even the earth under a construction site. Rarely are these soils purely dry or completely saturated; they exist in a more complex and dynamic state. These are partially saturated soils, where the water content is nonzero yet insufficient to achieve full saturation.
In this lecture, we delve into the realm of partially saturated soils. Our objective is twofold: to expand your conceptual understanding of soil-water interactions beyond the binary of 'dry' or 'fully wet' and to appreciate the nuanced ways in which partial saturation influences soil properties.
A comprehensive description of partially saturated soils requires consideration of many aspects of fluid-solid interaction at the microscale. A mere look at the phenomenological relationships - usually measured at the macroscale - is not sufficient for a deep understanding of the matter. Unfortunately, this depth cannot be covered in this course. While this course will provide an overview and introduction to this important topic, it's worth noting that the complete picture of partially saturated soils involves a depth of understanding that goes beyond our current scope. Nevertheless, our aim is to ignite curiosity and provide a foundational understanding of the key principles and considerations in dealing with partially saturated soils.
In partially saturated soils, four zones/states can be distinguished, as shown in below figures.
- The fully saturated zone lies below the water table: almost all pore spaces are filled with pore fluid, which can move freely or is bound to the soil particles by attractive forces of various origins. The fully saturated zone is bounded at the top by the water table. The pore water pressure \(p^w = 0\) kPa prevails along the water table (relative to atmospheric pressure). Below the water table, the pore water pressure increases linearly with depth (\(p^w(z) = \gamma^w z\), where \(\gamma^w\) is the unit weight of water, and \(z\) is the depth below the water table). However, a very small proportion of the pore space is filled by residual pore gas inclusions, known as residual air.
- Above the water table is the closed capillary zone, where all pore spaces are still filled with water. The pore water is bound by capillary forces in the pore channels and is therefore under tension despite full saturation (\(p^w < 0\) kPa). The closed capillary zone is limited upwards by the capillary rise, which can range from a few centimetres (sand) to several metres (clay), depending on the soil type. In both the fully saturated zone and the closed capillary zone, the weight of the soil acts as a buoyant force.
- Above the closed capillary zone is the partially saturated zone in which both pore fluids (pore water and pore gas) are mobile. The height of this zone depends largely on the soil's water tension properties. A relationship between the suction and the degree of saturation is provided by the Water Retention Curve (WRC), which is discussed in more detail in Saturation-suction relation.
- Soil particles above the area filled with capillary water may be surrounded by adhesive water which is held against gravity and, unlike free pore water, is immobile. In addition to the electrostatically and osmotically bound water, the pore angle water is also part of the adhesive water, which is bound by capillary forces at the contact points of the soil particles. The pore air is mobile.
Phase Boundaries and capillarity
In order to understand the influence of partial saturation on soil behaviour, we first need to better understand the interaction behaviour of the individual phases solid, water and air. For this purpose we distinguish between the interaction at the a) air-water interface and b) air-water-solid interface as illustrated in Figure 2.
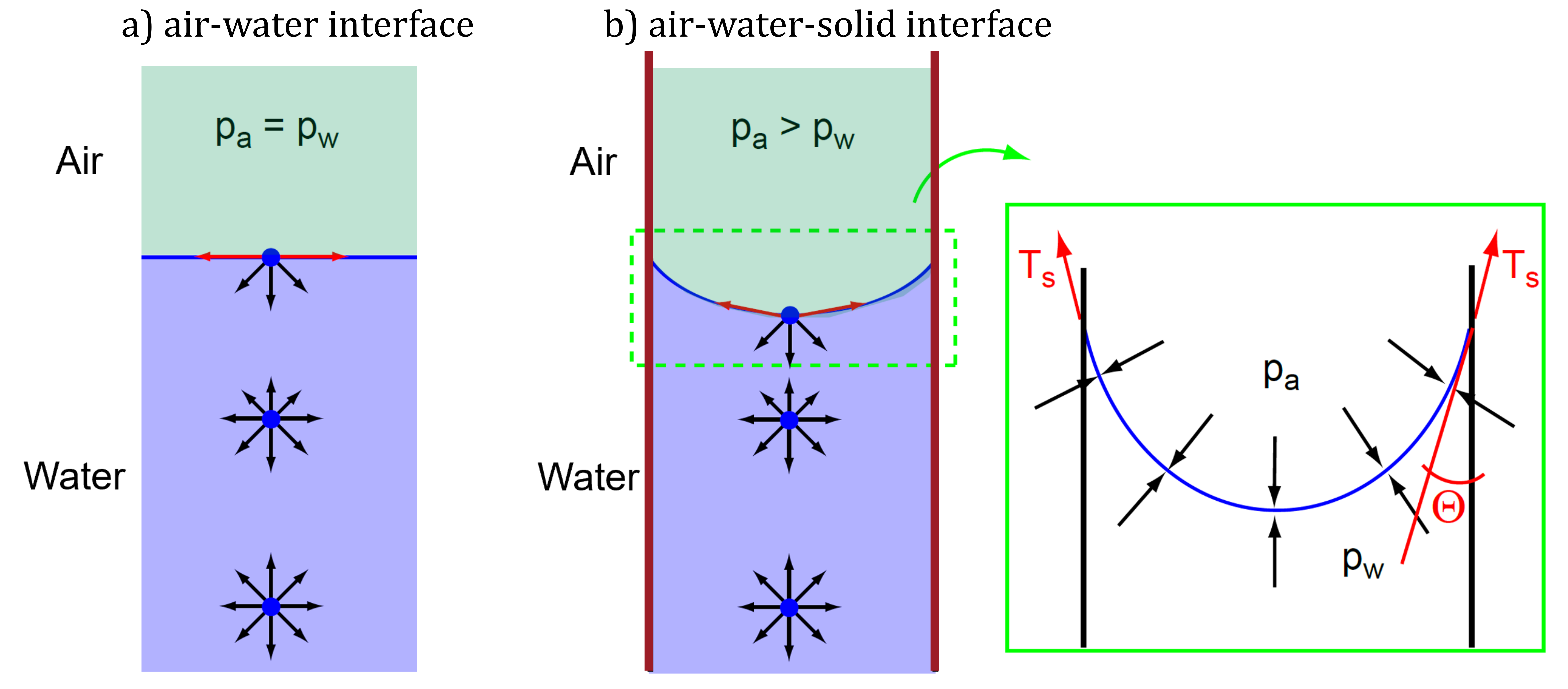Figure 2. Surface tension phenomenon at a) air-water and b) air-water-solid interface.
Water-air interface
Let us first consider the interface between water and air – without any solid as displayed in Figure 2 a). A liquid consists of molecules (blue dot in Figure 2). Attractive and repulsive forces (illustrated as arrows) act between these molecules. Within the volume of a liquid, the forces are balanced. Which is denoted here with arrows of equal length. At the interface between water and air, the density of the water changes abruptly in the range of just a few molecule lengths. This causes the repulsive forces in the water to also increase abruptly.
At the surface of the liquid, the symmetry is disturbed, that is, the molecules at the surface have no neighboring molecules in the vertical direction. With this in the vertical direction, only repulsive forces act on the molecules from below.
To maintain the balance of forces, the repulsive forces in the vertical direction are balanced by attractive forces. The resulting force of the molecules at the surfaces are thus directed inwards. Which then leads to the so-called surface tension \(T_s\) that results in the interface between the water and the air acting like a membrane under tension. Surface tension is measured as the tensile force per unit length of the contractile skin (i.e., units of mN/m). Surface tension is tangential to the contractile skin surface and the reason why water strider can walk on water.
The surface tension \(T_s\) decreases with increasing temperature. The value of \(T_s\) at different temperatures is given in below Table according to Kayne and Laby (1928)1.
| Temperature (°C) | Surface Tension, \(T_s\) in mN/m |
|---|---|
| 0 | 75.7 |
| 10 | 74.2 |
| 20 | 72.75 |
| 30 | 71.2 |
| 40 | 69.6 |
| 60 | 66.2 |
| 80 | 62.6 |
| 100 | 58.8 |
Water-air-solid interface
If the fluids come into contact with solid, three forces have to be considered:
-
First we have the surface tension at the interface between the pore air and the pore water
-
Then we have the attractive forces between the water molecules
-
And third there are adhesive forces acting between the solid and the fluid
If these attractive forces are larger than the others, the resulting forces is upwards directed. Fluids, such as water, where the attractive forces prevail are called wetting fluids. The upwards directed forces pull the water up at the interface to the solid. As a consequence, the interface between the water and the air becomes curved.
And whenever we have a curved surface there is a pressure difference. In this case, the air pressure is larger than the water pressure. The pressures acting on the membrane are \(p^w\) and \(p^a\). The membrane has a radius of curvature \(R_s\) and a surface tension \(T_s\). The horizontal forces along the membrane balance each other. Force equilibrium in the vertical direction requires that
Therein, \(2 R_s \sin \Theta\) is the length of the membrane projected onto the horizontal plane. The angle \(\Theta\) (see Figure 2) is known as the contact angle, and its magnitude depends on the adhesion between the molecules in the contractile skin and the material to which the fluid (water) is in contact. Following above equation, the pressure difference \(p^a-p^w\) is
where, for the 3D case, the radii of curvature of a warped membrane in two orthogonal principal planes are assumed to be identical, i.e. \(R_1=R_2=R_s\). For this pressure difference to develop, the pore water needs to rise in the tube such that a negative water pressure acts. This is the physical cause of the capillary rise of water in the soil.
Capillary rise
The capillary phenomenon is associated with the pressure difference \(p^a-p^w\). To introduce the concept of capillary rise, consider glass tubes of different diameter inserted into water under atmospheric conditions as displayed in Figure 3.
Water rises up in the tubes as a result of the surface tension of the contractile skin and the tendency of water to wet the surface of the glass tube. Capillary behavior can be analysed considering the vertical force equilibrium of the capillary water in the tubes:
The vertical component of surface tension \(F_{Ts,v}\) is responsible for holding the weight of the water column \(W_w\), which has a height \(h_c\). Above equation can be rearranged to give the maximum height of water in the capillary tube:
Considering that \(R_s = r/ \cos \Theta\), with the radius of the tube \(r\), the maximum capillary height is given by
From above equation it is clear, that the maximum capillary height depends on the radius (diameter) of the tube: the capillary height increases as the tube radius gets smaller.
If instead of a tube with constant diameter a so-called Jamin-tube with variable diameter is used for this experiment, it will be observed that the capillary height is different for wetting and drying processes. This effect is illustrated in slides 3 and 4 of Figure 3. When the end of the Jamin-tube is immersed in water, the water level in the tube rises to a height corresponding to the capillary rise height of a pipe of diameter \(d_2\). On the other hand, if the pipe is completely filled with water, the water level will fall to a height corresponding to the capillary rise height of a pipe of diameter \(d_1\). The capillary head during drainage is therefore determined by the small cross-sections, whereas the wide cross-sections determine the behaviour during wetting.
The capillary rise is different for the wetting and drying processes due to variations in capillary pore size.
Analogy to soils
The obvious question at this point is: Why are we concerned with water rise in tubes?
The structure of soils is very complex and difficult to describe in all its details. In a simplified consideration, we can think of the pore space in the soil as an assembly of tubes with very different diameters. From above observations, we can conclude that in narrow pore channels the water will rise higher than in pore channels with larger diameters. Empirical values for the height of capillary rise in natural soils during wetting or drying events are provided in below tables.
| Soil | Grain size (in mm) |
Capillary height \(h_c\) (in m) |
|---|---|---|
| Sand | 2.00 - 0.60 | 0.03 - 0.10 |
| 0.60 - 0.20 | 0.10 - 0.30 | |
| 0.20 - 0.06 | 0.30 - 1.00 | |
| Silt | 0.06 - 0.02 | 1.00 - 3.00 |
| 0.02 - 0.006 | 3.00 - 10.00 | |
| 0.006 - 0.002 | 10.00 - 30.00 | |
| Clay | < 0.002 | > 30.00 |
| Soil Type | Capillary Height \(h_c\) (in m) |
|---|---|
| Medium to Coarse Gravel | 0.05 |
| Sandy Gravel or Fine Gravel | ≤ 0.2 |
| Coarse Sand or Silty Gravel | ≤ 0.5 |
| Medium and Fine Sand | ≤ 1.5 |
| Silt | ≤ 5 |
| Clay | up to > 50 |
Surface tension has the ability to support a column of water, \(h_c\), in a capillary tube. The surface tension associated with the contractile skin places a reaction force on the wall of the capillary tube. The vertical component of this reaction force produces compressive stresses on the wall of the tube. The interface behaviour from the water column and the tube transfers to the interface behaviour of pore water and soil particles. Similar to the meniscy at the interface between the tube and the water, meniscy between the particles and the pore water form:
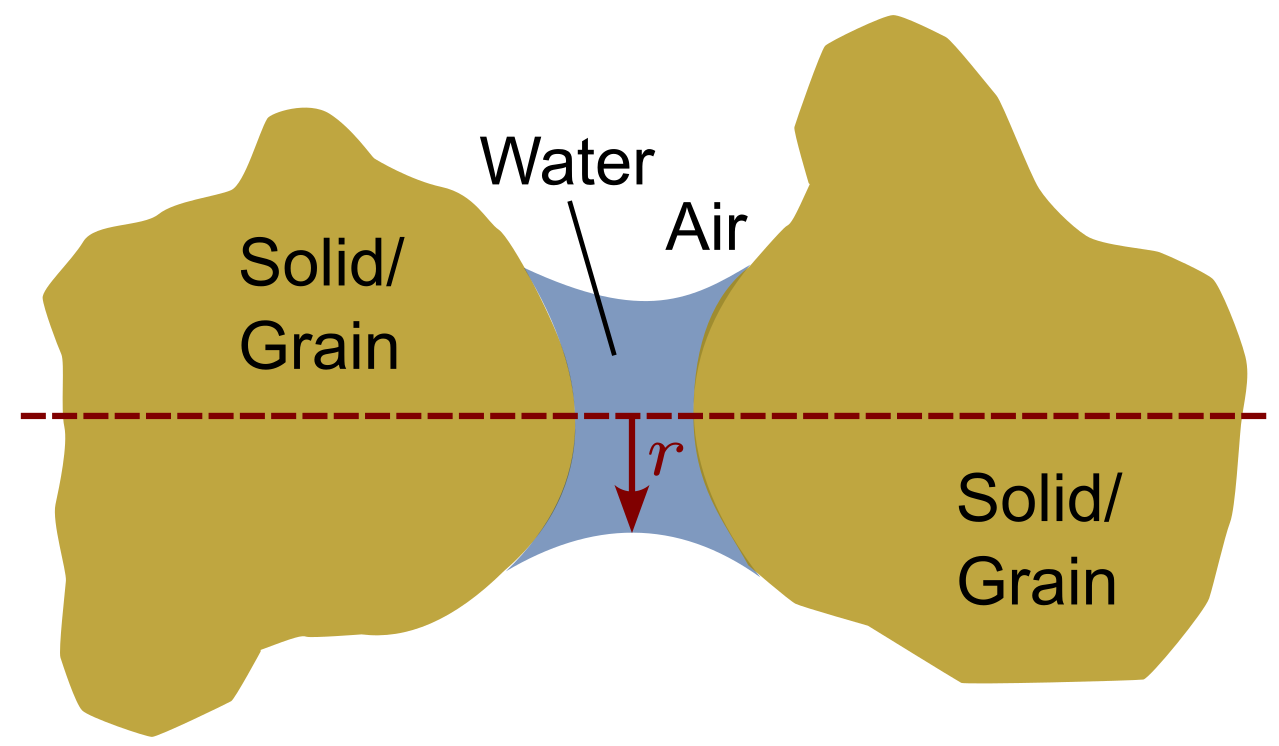
Figure 4. Water meniscy between two soil grains
The compressive stresses acting on the wall of the tube translate to an increase of the grain-to-grain forces and thus an increase in effective stress. Consequently, the presence of capillary pressure \(p^c=p^a-p^w\) in unsaturated soils produces a volume decrease and an increase in the shear strength of the soil. The extent of the additional effective stress due to the water in the contact zone between the two grains is discussed in the following section.
Effective stress in partially saturated soils
The effective stress concept for saturated soils has been introduced in section Effective stress. From the considerations in the previous section it becomes clear, that additional forces need to be taken into account for the calculation of the effective stress (grain-to-grain forces) in partially saturated soils. Various "effective" stresses have also been proposed for unsaturated soils in a form similar to the one for saturated soils
where \(s=p^a-p^w\) is the suction and \(\chi(S)\) an empirical factor depending on the degree of saturation \(S\). The primary objective is to find a definition of effective stress which allows to describe strength and stiffness of partially saturated soils as observed in laboratory tests. However, so far no scalar function \(\chi(S)\) was proposed that satisfactorily fulfils this objective.
Bishop effective stress
The relationship most often mentioned in this context is the so-called Bishop's stress. Although it is not a sufficient basis for describing the soil behaviour observed in laboratory experiments, we will discuss it in detail in the lecture. The reason for this is that it is the basis of all available computer programs for simulating partially saturated soils.
To derive the Bishop effective stress, we consider the idealised representation of two soil grains as spheres, as shown in Figure 5.
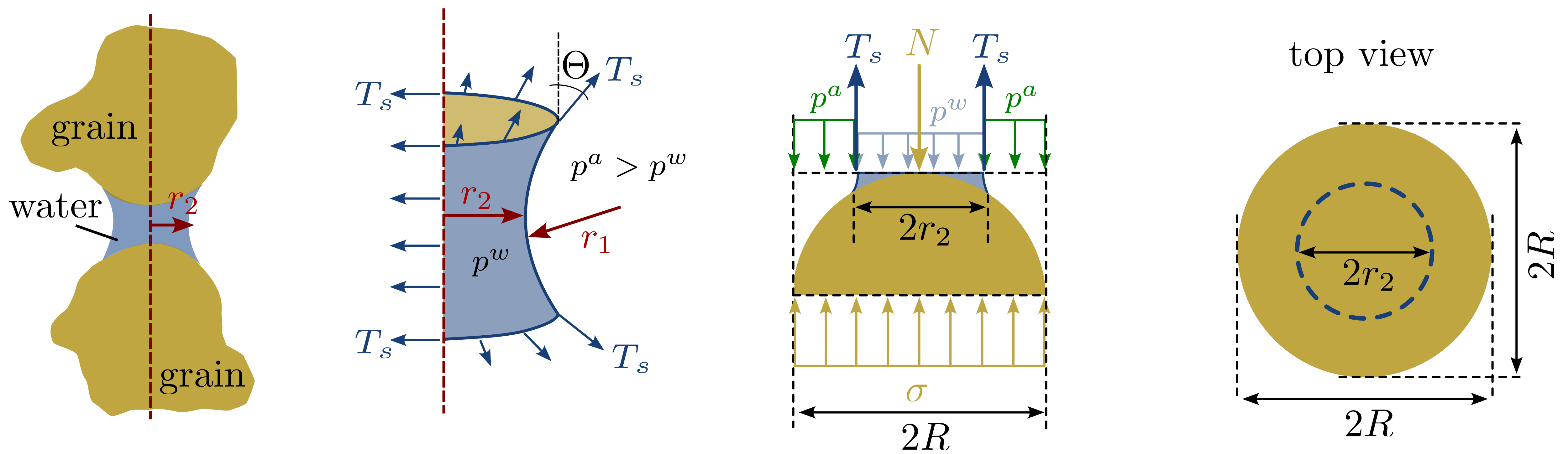
Figure 5. Idealised representation of two soil particles in the capillary zone being in contact with water
In above illustration, the radii of curvature are labelled \(r_1\) and \(r_2\), while the radius of a grain is labelled \(R\). \(N\) are the grain-to-grain (effective) forces in normal direction, \(\sigma\) is the total stress. From this representation, the following equilibrium of forces can be established in the vertical direction:
which reads in terms of effective stress
substituting \(T_s = (p^a-p^w) \left(\dfrac{1}{r_1}+\dfrac{1}{r_2}\right)\) in above equation yields
This corresponds to the formulation of Bishop (1959) with the parameter \(\chi\):
or in 3D
The difficulty in the above equation lies in determining the factor \(\chi\). As can be seen from the presented derivation, \(\chi\) performs the task of "geometrically weighting" the contribution of the suction \(s=p^a-p^w\) to the effective stress \(\sigma^\prime_{ij}\). This factor is difficult to determine for real soils, which has led to the development of various approaches to estimating \(\chi\).
The most commonly used relationship is \(\chi = S^\kappa\), where in most cases (and computer programs) \(\kappa = 1\). The advantage of linking the factor \(\chi\) to the degree of saturation \(S\) in this way is that the original formulation of effective stress is recovered at the limits:
- for completely dry soils, \(S = 0\) and \(\chi=0\) and thus \(\sigma_{ij}^\prime = \sigma_{ij} - p^a 1_{ij}\)
- for fully saturated soils, \(S=1\) and \(\chi=1\) and thus \(\sigma_{ij}^\prime = \sigma_{ij} + p^w 1_{ij}\)
Saturation-suction relation
At this point it should be clear that the suction \(s=p^a-p^w\) and degree of saturation \(S\) play an important role in describing the behaviour of partially saturated soils. The variation of saturation with respect to suction is defined by soil–water retention curve (SWRC). It is commonly presented in a graph of either gravimetric water content (\(w\)), volumetric water content (\(\theta_w\)) or degree of saturation (\(S\)) in the vertical axis against matric suction \(s\) in the horizontal axis in a logarithmic scale. Different methods exist to determine the SWRC for soils. In most methods, the suction in a soil sample is controlled/changed and the degree of saturation is measured. The methods differ in particular in the maximum suction that can be applied. A typical SWRC for granular soils is represented in Figure 6.
The SWRC in Figure 6 was obtained by draining water from an initially saturated soil sample (\(S=1\) and \(s=0\) kPa) by increasing the suction.
- During the first stage of the experiment, no change in saturation is observed although the suction was increased (\(s>0\) kPa).
- After further increasing the suction, water starts to drain from the soil sample and the degree od saturation decreases. The suction at which the water starts to drain out from the biggest soil pores is referred to as the air-entry value (AEV). The AEV has been found to depend on the grain size distribution of the soil. A larger proportion of fine particles implies smaller intra-particle pore spaces between soil particles, resulting in a higher AEV.
- With increasing suction, more water drains from the soil sample and the degree of saturation decreases (Phase 3). During drainage, the large pore channels drain first and, as the suction continues to increase, the pore channels with a narrower diameter drain as well - analogous to the observations in the Jamin-tube in section Capillary rise.
- At some point (Phase 4), further increase in suction does not result in any significant change in saturation. This point on the SWRC is referred to as the residual degree of saturation \(S^{res}\) or residual suction.
- The last slide of Figure 6 shows the observed behaviour for a wetting of the previously drained soil sample. As can be seen from the illustration a hysteresis exists between the drainage and the wetting curve. At the same suction, the soil contains more water during drainage than during wetting. The reason for this is that drainage is determined by the small pores, as these can retain the water at the passive capillary rise height. Wetting (rise of the water to the active capillary rise height), on the other hand, is determined by the large pores, as these cannot be overcome. See the observations for the Jamin-tube in section Capillary rise.
Measuring the SWRC in the laboratory
Mathematical description
Many different mathematical models exist linking the degree of saturation \(S\) to the suction \(s\). Alternatively, these models are sometimes formulated in terms of volumetric water content \(\theta_w\) instead of the degree of saturation \(S\). A widely used model is the one proposed by Van Genuchten3:
Therein, \(S^{sat}\) and \(S^{res}\) are the degree of saturation after a wetting process at zero suction and the residual degree of saturation at very high suctions, respectively. \(\alpha\), \(n\) and \(m\) are parameters controlling the shape of the SWRC. \(m=1-(1/n)\) is often assumed. \(\alpha\) controls the AEV, the smaller the value of \(\alpha\) the larger the AEV is. The parameter \(n\) controls the steepness of the transition zone. The influence of the models parameter are illustrated in Figure 7.
Shear strength of partially saturated soil
... to come ...
Hydraulic conductivity in partially saturated soils
The rate of flow of water through a porous medium is regulated by the hydraulic conductivity or coefficient of permeability of the soil. The hydraulic conductivity is the primary soil property required when analyzing steady-state and transient (or unsteady-state) flow of an incompressible fluid through a porous medium.
For saturated soils, the hydraulic conductivity is generally assumed to be a constant. However, the hydraulic conductivity for an unsaturated soil can change by several orders of magnitude depending on the degree of saturation of the soil.
An experiment illustrating this behaviour was performed by Mualem (1976)2. The experiment involved flowing water through glass beads subjected to different negative pore-water pressures, i.e. different suctions. The glass beads were initially saturated and then subjected to a series of steps with decreasing water pressures, i.e. increasing suction. At the different steps, the hydraulic conductivities of the glass beads and the degree of saturation was measured starting at saturated conditions. The results of this experiment are presented in Figure 8.
The results showed that the hydraulic conductivity of the glass beads started to decrease when the suction was approx. 3 kPa. A further increase in suction caused the hydraulic conductivity to rapidly decrease by several orders of magnitude from \(k^w\approx 2\cdot 10^{-2}\) m/s to \(k^w\approx 10^{-5}\) m/s.
The experiments of Mualem (1976) also show that the hydraulic conductivity is different for wetting and drying processes and that similar hysteretic effects are observed similar to the ones of the saturation-surction relation.
The reason for the decrease of the hydraulic conductivity is that water can only flow through that portion of a porous medium that consists of water. As the amount of water (i.e. the degree of saturation) in a soil decreases, the hydraulic conductivity decreases as well because there is less cross-sectional area through which water can flow. However, there is not a one-to-one relationship between the amount of water in the soil and the hydraulic conductivity. The hydraulic conductivity decreases at a much faster rate than the degree of saturation. The reason for this non-linear relation is that a reduction in the amount of water in the soil also increases the tortuosity of the flow path. As a consequence, an arithmetic decrease in the degree of saturation generally results in a logarithmic decrease in the hydraulic conductivity. A dry soil has a much lower hydraulic conductivity than a wet soil.
Mathematical description
Different methods for the estimation of the partially saturated hydraulic conductivity exist. Most methods rely on the concept of "relative permeability" where the hydraulic conductivity for various degrees of saturation \(k^{ps}\) is expressed as the product of the saturated hydraulic conductivity \(k^s\) and a relative permeability \(k^{rw}\):
where \(k^{rw}\) is most often assumed to be a function of the degree of saturation \(S\) and thus \(k(S)\). \(k^s\) is often assumed to be constant or depending on the porosity \(n\). Compared to the relative permeability \(k^{rw}\), the saturated hydraulic conductivity \(k^s\) is easier to measure. For the estimation of \(k^{rw}\) one often relies on empirical relations, two of which are discussed in more detail in the following subsections.
Cozeny/Carman
The famous Cozeny/carman model linking the saturated hydraulic conductivity \(k^s\) to the porosity \(n\) reads
Therein, \(C\) is a fitting parameter usually in the range of \(180-270\). \(\gamma_w\), \(\mu_w\) and \(d_e\) are the unit weight of water, the dynamic viscosity of water and the effective grain diameter, respectively. In a partially saturated soil, the pore space \(n\) is only partly occupied by water. The pore space that is occupied by water can be calculated as \(n_w = Sn\). In the saturated case (\(S=1\)) \(n_w=n\) and in the dry case (\(S=0\)) \(n_w=0\) hold. Considering \(n_w\) instead of \(n\) allows to apply the Cozeny/Carman relation to unsaturated soils:
With the definition of the relative permeability \(k^{rw}=k^{ps}/k^s\) we obtain:
Van Genuchten - Mualem
-
Kaye, G. W. C., & Laby, T. H. (1928). Tables of physical and chemical constants and some mathematical functions. Longmans, Green and Company Limited. ↩
-
Y. Mualem, ‘A new model for predicting the hydraulic conductivity of unsaturated porous media’, Water Resources Research, vol. 12, no. 3, pp. 513–522, Jun. 1976, doi: 10.1029/wr012i003p00513. ↩
-
M. Th. van Genuchten, ‘A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils’, Soil Science Society of America Journal, vol. 44, no. 5, pp. 892–898, Sep. 1980, doi: 10.2136/sssaj1980.03615995004400050002x. ↩