Galerkin method of weighted residuals

Several approaches exist to transform the physical formulation of the problem to its finite element discrete analogue. If the physical formulation of the problem is known as a differential equation then the most popular method of its finite element formulation is the Galerkin method of weighted residuals. If the physical problem can be formulated as minimization of a functional then variational formulation of the finite element equations is usually used. In the following we will focus on the Galerkin method of weighted residuals. The method of weighted residuals is based on the idea that the (unknown) solution \(u(x)\) of any function \(f(u,x)\) can be approximated by a linear combination (or the sum) of assumed trial functions \(\phi_J\) with unknown coefficients \(\tilde{u}_J\):

\[ \begin{equation}\label{eq:approx-solution} u(x) \approx u^*(x) = \sum_{J=1}^N \tilde{u}_J \phi_J(x) = \tilde{u}_1 \phi_1(x) + \tilde{u}_2 \phi_2(x) + ... + \tilde{u}_N \phi_N(x) \end{equation} \]

where \(u^*(x)\) is the approximation of \(u(x)\) and \(N\) is the number of terms (functions) in the approximation. The choice of trial functions \(\phi_J\) is arbitrary as long as they satisfy the essential boundary conditions. Note that the trial functions are functions in space \(\phi_J(x)\), the unknown coefficients \(\tilde{u}_J\), on the other hand, are discrete (point wise) values - which are at this stage unknown. \(\tilde{u}_J\) could also be regarded as the amplitude of the interpolation function \(\phi_J(x)\) or as the value of \(f\) at the \(J\)th position in space. Depending on the problem to be solved (or the underlying partial differential equation), the unknowns can be, for example, a displacement quantity, temperature or pore water pressure. They are often referred to as primary unknowns or degrees of freedom.

From a continuous problem to a discrete one

Note that by approximating the (true) solution by Eq. (\(\ref{eq:approx-solution}\)), the dimensionality of the solution is drastically reduced. Remember, the true solution is continuous, thus infinitely many solutions exist in the domain \(\Omega\). In contrast, the dimensionality of the approximated solution is equal to the number of test functions chosen, i.e. \(N\). In other words: at this stage we have transformed the continuous problem to a discrete one.

In principle, this procedure is identical to the approximation of a function \(f(x)\) by a Taylor series with which you are familiar. Here the function is represented as an infinite sum of terms. These terms are expressed in terms of the function's derivatives at a single point \(x^*\):

\[ T_{f(x,x^*)} = \sum_{I=0}^\infty \frac{f^{'(I)}(x^*)}{I!}\left(x-x^*\right)^I \]

For the evaluation of the Taylor series, one restricts oneself to a maximum of \(n\) terms. The special case of \(n=2\) terms is also called "linearisation of \(f\) at the point \(X^*\)", we will encounter this again in Section Newton-Raphson method.

\[ T^N_{f(x,x^*)} \approx \sum_{I=0}^N \frac{f^{'(I)}(x^*)}{I!}\left(x-x^*\right)^I = f(x^*) + f'\left(x-x^*\right) + \frac{f"}{2!}\left(x-x^*\right)^2 + ... + \frac{f^{'(N)}(x^*)}{N!}\left(x-x^*\right)^N \]

For a better understanding, an exemplary application of the approximation is shown graphically for illustration in Figure 1. For this purpose, an arbitrary one-dimensional differential equation \(D(u,x)\) (shown in blue) with the (exact) solution \(u(x)\) is considered.

Figure 1. Schematic of the approximation of the true solution \(u(x)\) with a linear combination \(u^*(x)\) of basis functions \(\phi_I(x)\) with coefficients \(\tilde{u}_I\) (discrete points).

The solution of \(D(u,x)\) is approximated by the linear combination \(u^*(x)\) as defined in Equation (\(\ref{eq:approx-solution}\)). Three functions \(\phi_I(x)\) (shown in red) with the three unknown coefficients \(\tilde{u}_I\) are used for the approximation. Simplified linear functions are chosen for \(\phi_I(x)\). It becomes clear that the actual solution \(u(x)\) agrees with the approximated solution only at the positions of the coefficients \(\tilde{u}_I\). At all other positions there is a more or less large discrepancy between the approximation \(u^*(x)\) and the actual solution \(u(x)\). By choosing linear functions \(\phi_I(x)\), this discrepancy is very pronounced, since the course of \(u(x)\) is strongly non-linear. The choice of higher order functions would have led to a better result here, more on this later. Figure 1 also shows how the value of the approximated solution at any coordinate \(x_{\star}\) can be evaluated by evaluating Equation (\(\ref{eq:approx-solution}\)) at position \(x_{\star}\).

Next, Equation (\(\ref{eq:approx-solution}\)) is substituted in the PDE \(D(u,x)\) (e.g. the balance of linear momentum). However, since the approximation is not exact at every point in the domain, a residuum \(R\) is obtained (the difference from the exact solution, so to speak):

\[ \begin{equation}\label{eq:fem-error} R(u^*(x),x) = D(u^*(x),x). \end{equation} \]

The residual \(R\) is a continuous function of \(X\) and \(u\) in the general case and tells us by how much the approximate solution \(u^*(x)\) does not satisfy the PDE. If \(u^*(x)\) were exact, the residual vanishes \(R=0\) for all \(x\). At this point we now have one equation with \(N\) unknowns, which is not solvable. Instead, we require a weighted integral of the residual to zero in an average sense over the domain. A weighted residual is simply the integral over the domain of the residual \(R(x)\) multiplied by a weight function \(\psi(x)\):

\[ \begin{equation}\label{eq:fem-error-weighted} \int_\Omega \psi(x) R(u^*(x),x) dv = 0. \end{equation} \]

By choosing \(N\) weight functions, \(\psi_I(x)\) for \(I=1,2,...N\), and setting these \(N\) weighted residuals to zero, we obtain \(N\) equations (as many linearly independent equations as there are linear independent weight functions):

\[ \begin{align}\label{eq:fem-error_2} R_1(u^*(x),x) &= \int_\Omega \psi_1(x) D(u^*(x),x) = 0 \nonumber \\ R_2(u^*(x),x) &= \int_\Omega \psi_2(x) D(u^*(x),x) = 0 \\ &\vdots \nonumber \\ R_N(u^*(x),x) &= \int_\Omega \psi_N(x) D(u^*(x),x) = 0 \nonumber \end{align} \]

By doing so, we obtain a system of \(N\) equations that we can solve to determine the \(N\) unknowns \(\tilde{u}_J\) (\(J=\{1,2,...N\}\)). The task now is to determine the constants \(\tilde{u}_J\) in Eq. (\(\ref{eq:approx-solution}\)) in such a way that the residual \(R(x)\) disappears or is minimized. In the method of weighted residuals, the next step is to determine appropriate weight functions \(\psi_I(x)\). A common approach, known as the Galerkin method, is to set the weight functions equal to the functions used to approximate the solution: \(\phi_I(x) = \psi_I(x) = N_I(x)\):

\[ \begin{align} u(x) \approx u^*(x) &= \sum_{I=1}^N \tilde{u}_I N_I(x), \\ R_I(u^*(x),x) &= \int_\Omega N_I(x) D(u^*(x),x) = 0 ~~~\text{with:}~ I = \{1,2,...N\}. \label{eq:weighted-integral} \end{align} \]

Up to this point we have looked at the general procedure using an abstract one-dimensional partial differential equation \(D(u^*(x),x)\). If we now apply this procedure to the two-dimensional boundary value problem of the earth dam under earthquake load described at the beginning, the following results:

\[ \begin{align} u_i(x) \approx u_i^*(x) &= \sum_{I=1}^N \tilde{u}_{Ii} N_I(x_i), \\ R_I(u_i^*(x_i),x_i) &= \int_\Omega N_I(x_i) D(u^*_i(x_i),x_i) = 0 ~~~\text{with:}~ I = \{1,2,...N\}, \\ &~~ \text{where:} ~~D(u_i^*(x_i),x_i) = \rho \ddot{u}^*_i - \frac{\partial \sigma_{ij}(u^*_i)}{\partial x_j} - \rho b_i. \end{align} \]

Notice the difference in indices: capital indices such as \(I,J\) are simple counters (1,2,3,4,5,...) whereas small indices such as \(i,j=\{1,2\}\) denote dimensions in space. Consequently, \(\tilde{u}_{Ii}\) denotes the \(i\)th component of the unknown solution \(u^*\) at point \(I\). Even if the procedure seems complicated at first sight, its application to a three-dimensional problem or another PDE is straight forward. The result is the transformation of a continuous problem whose solution is a function into a system of \(N\) equations with \(N\) unknowns. Only in this way does an approximate solution of the problem become possible at all. The question remains what functions (and how many) to choose for \(N_I(x)\), which will be discussed in the next Section.

---

A simple example (string sagging under a linearly increasing load)

In this illustrative problem we imagine a light, perfectly flexible string that spans the horizontal \(x\)-axis from the left support at \(x=0\) to the right support at \(x=L\). The string is pulled taut by a constant axial tension \(T\) (newtons) and is subjected to a vertical, downward‐acting distributed load whose intensity increases linearly along the span, \(q(x)=q_0\,x/L\). With small deflections the vertical force balance on an infinitesimal element \(\mathrm dx\) is simply \(T\,u''(x)=-q(x)\), where \(u(x)\) denotes the downward displacement. Both ends of the string are pinned, so \(u(0)=u(L)=0\).

Figure 2. Example: String sagging under a linearly increasing load.

To keep the algebra transparent we non‑dimensionalise the model: measure length in units of \(L\) (\(x\mapsto x/L\)), let downward displacements remain positive, and choose units so that \(T=1\) and \(q_0=1\). In these scaled variables the boundary‑value problem reduces to

\[ u''(x)=-\,x,\qquad 0\le x\le 1,\qquad u(0)=u(1)=0, \]

which is the starting point for the Galerkin weighted‑residual demonstration.

Step 1 – choose a trial (shape) function

Pick the smallest polynomial that satisfies both boundary conditions:

\[ u^*(x)=a\,x(1-x)=a\,(x-x^{2})\quad(\text{one unknown }a). \]

Step 2 – compute the residual

Insert \(u^*\) into the differential equation:

\[ R(x)=(u^*)''(x)+x=-2a+x. \]

Step 3 – pick the weight function
For the Galerkin variant we set \(w(x)\) equal to the shape function:

\[ w(x)=x(1-x). \]

Step 4 – enforce the weighted‑residual condition

\[ \int_{0}^{1} w(x)\,R(x)\,dx=0 \;\;\Longrightarrow\;\; \int_{0}^{1}(x-x^{2})(-2a+x)\,dx=0. \]

Step 5 – evaluate the integral and solve for \(a\)

Expand the integrand: \((-2a+x)(x-x^{2})=-2a(x-x^{2})+x^{2}-x^{3}\).

• \(\displaystyle\int_{0}^{1}-2a(x-x^{2})\,dx=-2a\Bigl[\tfrac12-\tfrac13\Bigr]=-\,\frac{a}{3}\)
• \(\displaystyle\int_{0}^{1}(x^{2}-x^{3})\,dx=\Bigl[\tfrac13-\tfrac14\Bigr]=\frac1{12}\)

Set their sum to zero:

\[ -\frac{a}{3}+\frac1{12}=0\;\;\Longrightarrow\;\;a=\frac14. \]

Step 6 – write the approximate solution

\[ \boxed{\,u^*(x)=\frac14\,x(1-x)\,}\qquad(\text{for }T=1). \]

Consistency check

A comparison of the approximate solution with the exact solution is depicted in Figure 3.

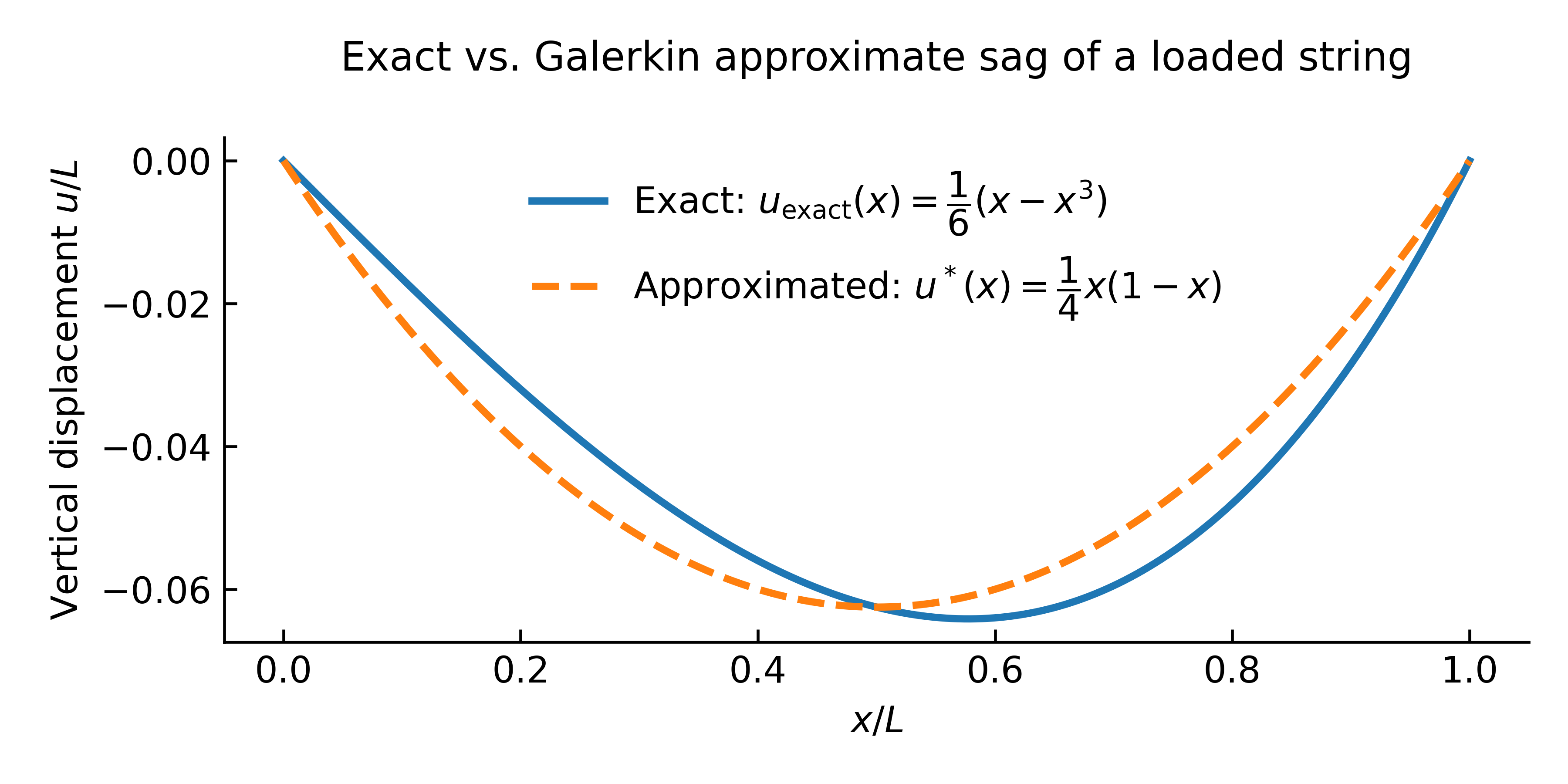
Figure 3. Galerkin approximate vs. exact sag of a loaded string.

Observe that the exact and approximate curves coincide at the two supports and at the midpoint:

• At the boundaries \(x=0\) and \(x=1\) the match is trivial because both functions satisfy the same essential boundary conditions.
• At the midpoint \(x=\tfrac12\) the match is a genuine interpolation property: with only one interior degree of freedom the quadratic projects the cubic part of the exact solution so that the weighted residual vanishes. Geometrically that pushes the error curve to cross zero at the centre.

Mathematically this can be shown by examining the difference between the exact solution \(u(x)\) and the approximate solution \(u^*(x)\):

\[ \begin{aligned} e(x)&=u_{\text{exact}}(x)-u^*(x) \\ &=\frac{-1}{12}\;x\,(1-x)\,(2x-1). \end{aligned} \]

Hence \(e(x)=0\) at

\[ x=0,\;x=\tfrac12,\;x=1. \]

Except at these three points, the curves differ. In particular, the true maximum sag occurs at \(x \approx 0.63\), whereas the single-term approximation under-predicts that peak.

The reason the midpoint is captured exactly is twofold: the cubic term in the exact solution vanishes at both ends, and the Galerkin condition enforces orthogonality of the residual to the quadratic weight \(x(1-x)\). For a cubic error function, that orthogonality guarantees one interior root—and, by symmetry, it falls at \(x=0.5\). Adding higher-order shape functions yields more matching points; with the full cubic basis, the approximation becomes exact everywhere.