Effective stress in saturated soils

Terzaghi & Fillunger

The decomposition of total stress into effective stress and pore water pressure is a cornerstone of today's geotechnical field. This concept stems from the experimental observations of Karl von Terzaghi, who meticulously investigated the behavior of soils under various loading conditions. Terzaghi observed that upon applying a load to saturated soil, water was expelled from the voids over time, a phenomenon known as consolidation. He postulated that both the rate and degree of consolidation were significantly influenced by the effective stress—the component of stress directly borne by the soil grains. He further articulated that the strength and deformation behavior of soils weren't determined by the total stress, but rather by the effective stress, which is the difference between the total stress and the pore water pressure within the soil voids.

While the effective stress principle is predominantly attributed to Karl von Terzaghi, Paul Fillunger, a colleague of Terzaghi, concurrently delved into similar terrain. Fillunger emphasized the mechanical interactions of soil particles. He too recognized the role of pore water but contended that the primary mechanisms of soil deformation and strength arose from the reorientation and sliding of soil particles. In Fillunger's perspective, hydraulic shifts, such as variations in pore water pressure, emerged as a consequence of these mechanical changes, taking a more secondary role in soil behavior.

Their concurrent but differing insights inevitably led to intellectual disputes¹. While both were rooted in empirical observations, Terzaghi's emphasis on the hydraulic attributes of soils and Fillunger's leaning towards the mechanical intricacies brought about contrasting paradigms. As soil mechanics evolved, history has placed Terzaghi in a more prominent position.

Theoretical considerations

For the theoretical derivation of the effective stress concept let us consider a representative volume element of saturated soil as depicted below.

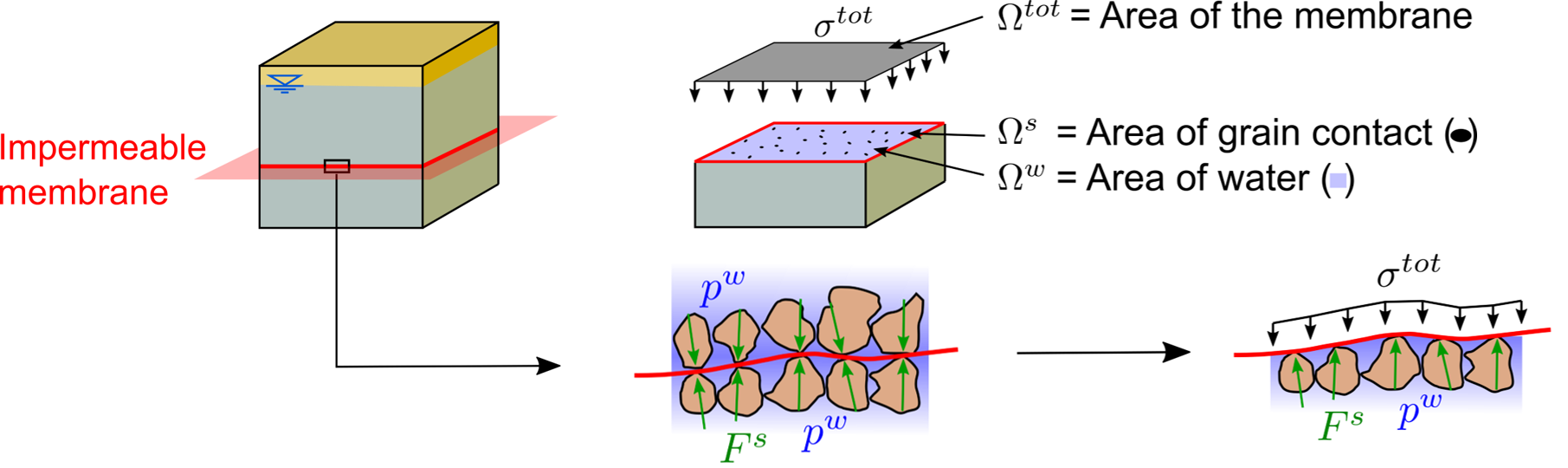
• In the simplified micro-mechanical representation the forces acting in the saturated soil body are depicted. The green arrows represent the grain-to-grain forces \(F^s\) acting between the individual particles. Both, the solid grains as well as the pore water are considered to be incompressible. The pore water pressure \(p^w\) is a hydrostatic stress, e.g. acting in all directions with the same magnitude
• We first divide the soil into two parts by placing an imaginary impermeable transparent membrane in-between these two parts. The membrane is placed as straight as possible but is not allowed to cut through the particles.
• The area of the membrane inside the soil element corresponds to the total area of the cross section \(\Omega^{tot}\). Looking in plane view on the membrane, we see a very large blue area and many very small black dots. The blue are corresponds to the area of water \(\Omega^w\) while the black dots represent the grain contacts. The area of all grain contacts together is denoted as \(\Omega^s\).
• From the view point of the soil beneath the membrane, the soil volume above the membrane (since hydraulically decoupled) exerts an external homogeneous load resulting from the dead weight of the pore water and solid grains that has to be carried by the pore water pressure and grains below the membrane.

Requiring the soil to be in static equilibrium the sum of all vertical forces is nil, i.e.

\[ \sum F_v = 0 \]

which yields

\[ \sigma^{tot} \Omega^{tot} = \sum F^s + p^w \Omega^w \]

We can rewrite above equation considering that \(\Omega^{tot} = \Omega^w + \Omega^s\) to

\[ \sigma^{tot} \Omega^{tot} = \sum F^s + p^w \left(\Omega^{tot}-\Omega^s\right) \]

and dividing by \(\Omega^{tot}\) yields

\[ \sigma^{tot} = \frac{F^s}{\Omega^{tot}} + p^w \frac{\Omega^{tot}-\Omega^s}{\Omega^{tot}} \]

Considering that the area of the grain-to-grain contacts is negligibly small compared to the total area \(\Omega^s \approx 0\) finally yields:

\[ \sigma^{tot} = \frac{F^s}{\Omega^{tot}} + p^w \]

identifying the area averaged grain-to-grain forces as the effective stress \(\sigma^\prime = \frac{F^s}{\Omega^{tot}}\) yields the well known equation of effective stress:

\[ \sigma^{tot} = \sigma^\prime + p^w \]

or in 3D:

\[ \sigma_{ij}^{tot} = \sigma_{ij}^\prime + \delta_{ij} p^w \]

Biot

While Terzaghi's effective stress concept assumes both the pore fluid (typically water) and the soil grains to be incompressible, this assumption doesn't universally apply, especially when considering materials beyond soils, like rocks or even concrete. Specifically, Terzaghi's concept relies on the idea that the stiffness of individual grains, denoted as \(K^s\), is much larger than the stiffness of the assembled grain skeleton or solid matrix, represented as \(K\). In essence, it assumes \(K^s \gg K\).

However, many geomaterials, especially rocks, and other porous media, such as concrete, don't strictly follow this principle. Maurice Biot's recognized the potential influence of the compressibility of different phases in porous media on the effective stress and introduced a new parameter, \(\alpha\), to address it. The effective stress, as given by Biot, is:

\[ \sigma_{ij}^{tot} = \sigma_{ij}^\prime + \alpha \delta_{ij} p^w ~~~ \text{with} ~~~ \alpha = 1 - \frac{K}{K^s} \]

In situations where the solid matrix's stiffness is significantly less than that of the individual grains—as is typical for soils—the value of \(\alpha\) approaches 1. This brings Biot's equation in line with Terzaghi's original effective stress formula. However, for materials like many rocks or concrete, \(\alpha\) can vary, often ranging between 0.5 and 0.9.

References

---

1. R. de Boer, Theory of Porous Media. Berlin, Heidelberg: Springer Berlin Heidelberg, 2000. doi: 10.1007/978-3-642-59637-7. ↩