Skip to content

Influence of mean effective pressure

So far, our discussion has been focused on the effects of density and loading direction (compression versus extension) on the behaviour of sands under both drained and undrained conditions. We have not yet delved into the influence of mean effective pressure \(p^\prime\), also known as barotropy or pressure dependency. Next, we will expand our analysis of the previous triaxial test results by incorporating data from tests conducted on samples subjected to higher initial mean effective stresses.

Drained triaxial compression

The results of four drained triaxial compression tests on sand samples of different initial densities and at different initial mean effective pressures \(p^\prime_0=100\) kPa and \(p^\prime_0=400\) kPa are summarized in below animation. The observations are explained after the animation.

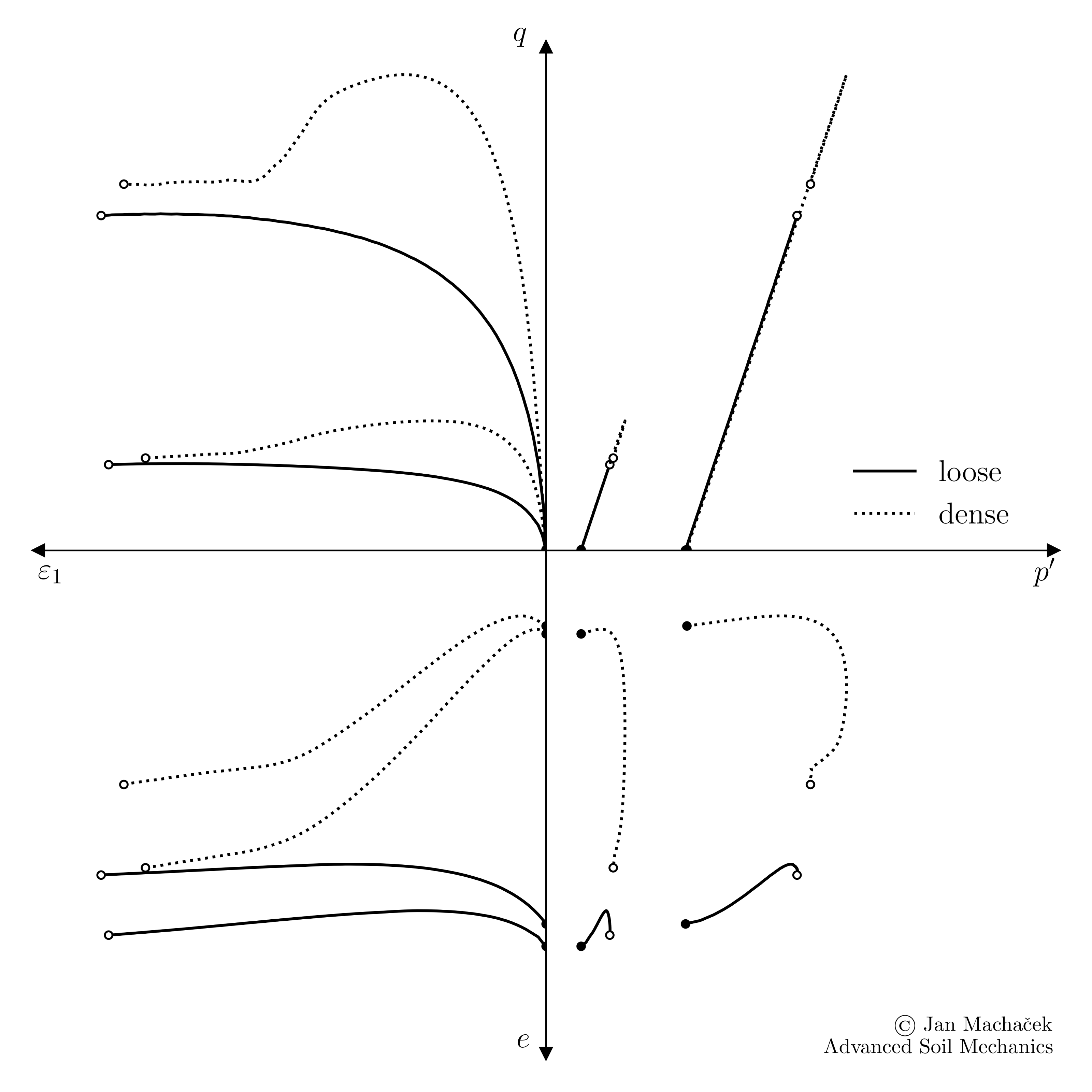Typical results of a monotonic triaxial test on loose and dense sand for two different initial mean effective pressures \(p^\prime_0\) in the \(\varepsilon_1-\varepsilon_v\) plane and \(p^\prime-e\) plane (click to play)

Observations

  • Comparing the test results of the loose samples, it becomes evident that the initial mean effective pressure \(p^\prime_0\) has a significant influence on the shear strength at the residual state. For instance, the loose sample with an initial mean effective pressure of \(p^\prime_0 = 100\) kPa reaches a maximum deviatoric stress of \(q_r(p^\prime_0=100) = 250\) kPa. In contrast, a sample of similar density but with a higher initial mean effective pressure of \(p^\prime_0 = 400\) kPa achieves a substantially greater maximum deviatoric stress of \(q_r(p^\prime_0=400) = 970\) kPa.
  • Furthermore, at the residual state, it is observed that the deviatoric stress \(q_r\) for all samples aligns closely with predictions made by the Mohr-Coulomb failure line described by the inclination \(M_c\). For more details, including the dense samples' deviation from the failure line, readers are directed to the section on Consolidated Drained Monotonic Triaxial Tests on Sand.
  • Focusing on the behaviour of the dense samples, both exhibit a distinct peak strength followed by strain softening independent of the initial mean effective pressure. Closer examination reveals that the peak is less pronounced for the sample with a higher \(p^\prime_0\). While this difference is subtle in the presented example, Lade and Bopp2 demonstrate that this effect becomes more pronounced with increasing \(p^\prime_0\), in their studies covering a range from \(p^\prime_0=250\) kPa to \(p^\prime_0=60\) MPa.
  • In the \(e-p^\prime\) plane, the influence of mean effective pressure on the behaviour of sand is evident when observing dense and loose samples. Dense samples subjected to high mean effective pressures tend to exhibit a smaller increase in void ratio upon shearing, indicating reduced dilatancy compared to when these samples are subjected to lower pressures. In contrast, loose samples under high pressures demonstrate a more pronounced decrease in void ratio, signifying greater contractive behaviour than their counterparts compressed under lower pressures.

Undrained triaxial compression and extension

The influence of mean effective stress \(p^\prime\) on the behaviour of sands under undrained conditions is demonstrated in below figure. This figure shows the results of two undrained triaxial compression and extension tests conducted on dense sand samples at different initial mean effective pressures \(p^\prime_0\).

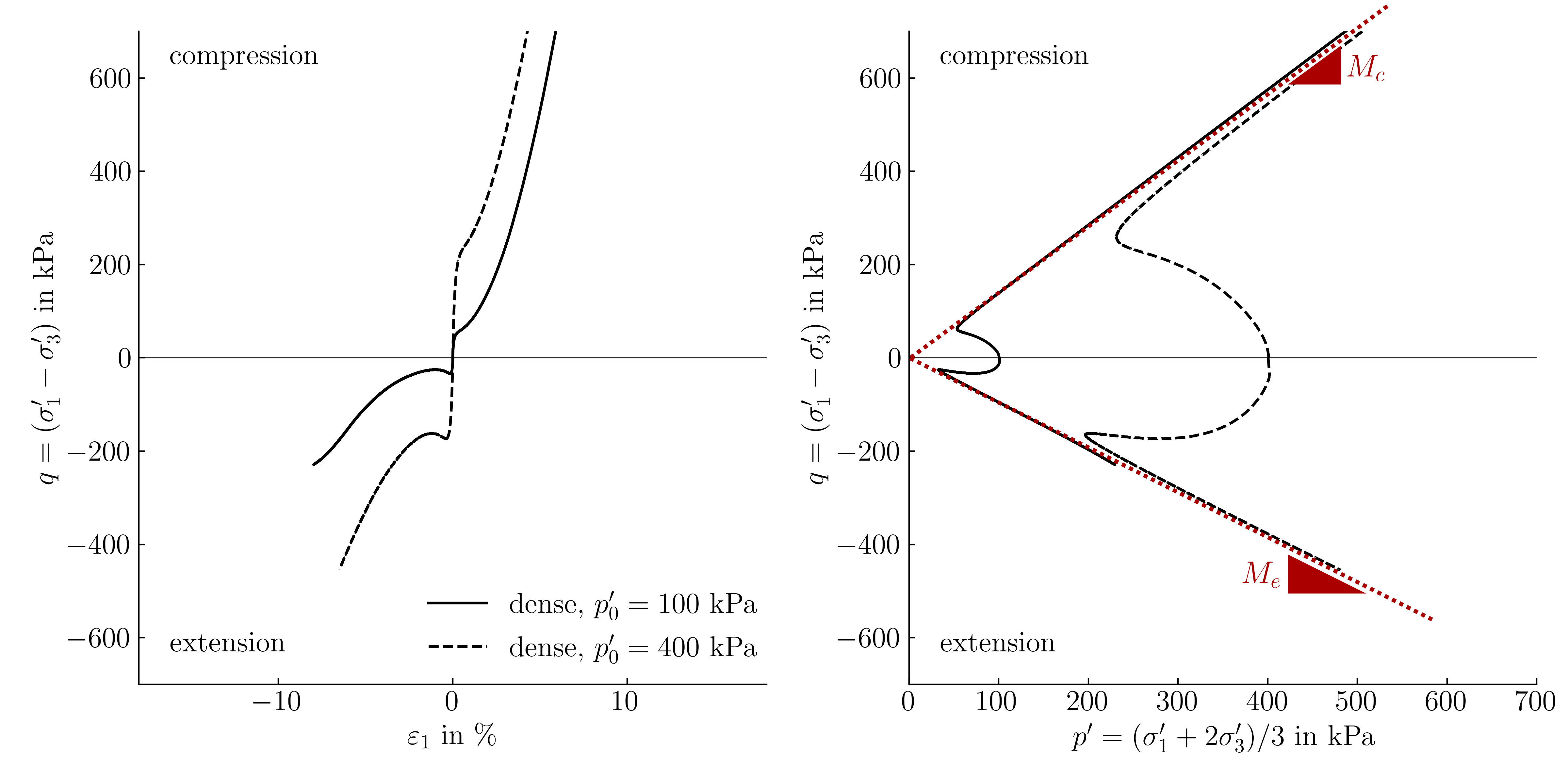triax-cu-density-stress Typical results of undrained monotonic triaxial compression and extension tests on sand in the \(\varepsilon_1-q\) plane and \(p^\prime-q\) plane for two different initial mean effective pressures

Observations

Consistent with findings from drained triaxial compression tests, a significant increase in shear strength with increasing initial mean effective pressures is observed. Furthermore, at the critical state, the stress ratios closely conform to the Mohr-Coulomb failure criterion, as evidenced by their alignment with the failure envelope's inclination, denoted by \(M_c\) in compression and \(M_e\) in extension—with \(M_e\) generally being less than \(M_c\).

  1. T. Wichtmann and T. Triantafyllidis, ‘An experimental database for the development, calibration and verification of constitutive models for sand with focus to cyclic loading: part I—tests with monotonic loading and stress cycles’, Acta Geotech., vol. 11, no. 4, pp. 739–761, Aug. 2016, doi: 10.1007/s11440-015-0402-z. ↩

  2. P. V. Lade and P. A. Bopp, ‘Relative density effects on drained sand behavior at high pressures’, Soils and Foundations, vol. 45, no. 1, pp. 1–13, Jan. 2005, doi: 10.3208/sandf.45.1_1. ↩