Soil behaviour under undrained cyclic shearing

Undrained cyclic triaxial test

Undrained cyclic triaxial tests share similarities with their monotonic counterparts in terms of sample preparation, geometry, and the testing apparatus used. However, unlike monotonic triaxial tests where loading is applied in a single direction (either in compression or extension), cyclic triaxial tests involve alternating loading, such as compression-extension-compression cycles. These tests can be initiated from either isotropic ($\sigma_1 = \sigma_3$) or anisotropic ($\sigma_1 \neq \sigma_3$) stress states and can be conducted under either stress-controlled or strain-controlled conditions. In stress-controlled tests, the following procedures are typically followed:

The top cap of the apparatus is displaced at a constant rate, inducing a consistent shear strain rate in the sample.
During shearing, the axial force and consequently the stress within the sample are continuously monitored.
Upon the measured stress reaching a predetermined target value, the direction of displacement is reversed (for example, switching from compression to extension).
The reversal of displacement direction is repeated for a specified number of cycles or until a certain soil behavior is observed, such as the onset of liquefaction or significant degradation of stiffness.
Throughout the test, pore water pressure is also measured, which is crucial in undrained conditions to understand the soil's response to cyclic loading and its potential for liquefaction.

Typical test results of an undrained cyclic triaxial compression test on loose sand are represented in the following animation, illustrating the development of axial stress $\sigma_1$, radial stress $\sigma_3$, pore water pressure $p^w$, and axial strain $\varepsilon_1$. The applied stress amplitude to the sample is $\Delta \sigma_1 = q^{ampl} = 25$ kPa. Note that these are total stresses. The initial effective stresses are defined as $\sigma_1^\prime = \sigma_1-p^w=100$ kPa and $\sigma_3^\prime = \sigma_3-p^w=100$ kPa, resulting in a mean effective stress at the beginning of the test of $p^\prime_0 = 100$ kPa.

Development of (total) stresses $\sigma_1$ and $\sigma_3$, pore water pressure $p^w$ and axial strain $\varepsilon_1$ during an undrained cyclic triaxial test on sand.

From the above simulation, we observe that the axial stress $\sigma_1$ (blue) oscillates around its mean value of 600 kPa, with maximum and minimum values of 625 and 575 kPa, respectively. The radial stress $\sigma_3$ (green) remains constant throughout the test. The axial stress cycles correspond with fluctuations in pore water pressure $p^w$ (red). However, unlike $\sigma_1$, the mean value of $p^w$ increases with each loading cycle. In terms of effective stress, this increase in pore water pressure with each loading cycle results in a decrease of the mean effective stress. At the test's final stage, the condition $\sigma_1 = \sigma_3 = p^w$ is reached, leading to zero mean effective stress $p^\prime=0$. Regarding axial strain $\varepsilon_1$ (blue, bottom), initial loading cycles produce only small strain amplitudes. However, as the cyclic loading continues, an increase in strain amplitude is observed, peaking when $p^w$ approaches $\sigma_1$ and $\sigma_3$.

Initially, the time per cycle ($\sigma_1: 600 \rightarrow 625 \rightarrow 600 \rightarrow 575 \rightarrow 600$ kPa) is almost consistent. As the strain amplitude increases, so does the time per loading cycle, reflecting the progressive decrease in stiffness and the constant displacement rate condition.

Behaviour of sands

... yet to come ...

Behaviour of fine-grained soils

So far, we have concentrated on the behavior of sands under undrained cyclic loading. However, as we have already seen with monotonic loading, fine-grained soils are expected to behave differently than their granular (coarse-grained) counterparts, especially with increasing plastic fines content. Typical test results for normally consolidated, medium-plastic fine-grained soils under isotropic conditions are shown in the figure below (experimental data from ²).

Development of (total) stresses $\sigma_1$ and $\sigma_3$, pore water pressure $p^w$, and axial strain $\varepsilon_1$ during an undrained cyclic triaxial test on Kaolin. (click to play)

In the first part of the test, we observe behaviour similar to that in the sand test: ongoing cyclic loading leads to an increase in the mean value of pore water pressure $p^w$. Compared to the test on sand, the increase in strain amplitude is more gradual in fine-grained soils. Contrary to the tests on sand, full liquefaction ($\sigma_1=\sigma_3=p^w \rightarrow p^\prime=0$) is not reached. Observing the test results in the $p^\prime-q$ plane, an eight-shaped stress loop is seen, not reaching $p^\prime=q=0$ (as opposed to the butterfly-shaped stress loop in sand). The increase in strain amplitude with decreasing $p^\prime$ is evident on the right-hand side of the figure.

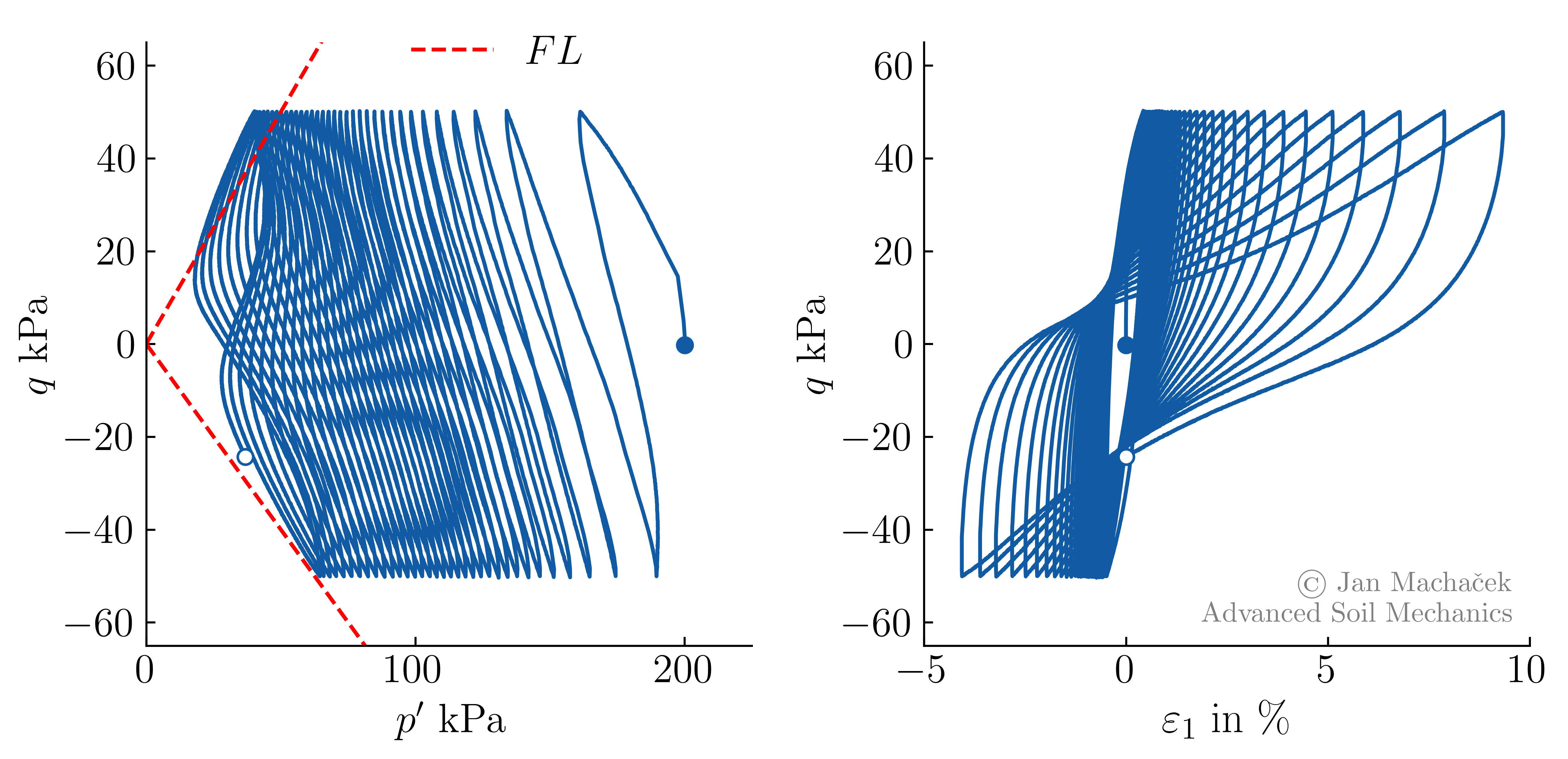
Undrained cyclic triaxial test on normally consolidated Kaolin: deviatoric stress $q$ over mean effective pressure $p^\prime$ (left) and over axial strain $\varepsilon_1$ (right), FL = Failure Line from monotonic tests.

A typical result from a test with anisotropic consolidation in the triaxial compression regime ($q_0=50$ kPa at $p_0^\prime=200$ kPa) is shown below. OCR and $q^{ampl}$ are the same as in the test under isotropic conditions shown above. In this test, the minimum deviatoric stress remained positive, i.e., $\sigma_1 > \sigma_3$.

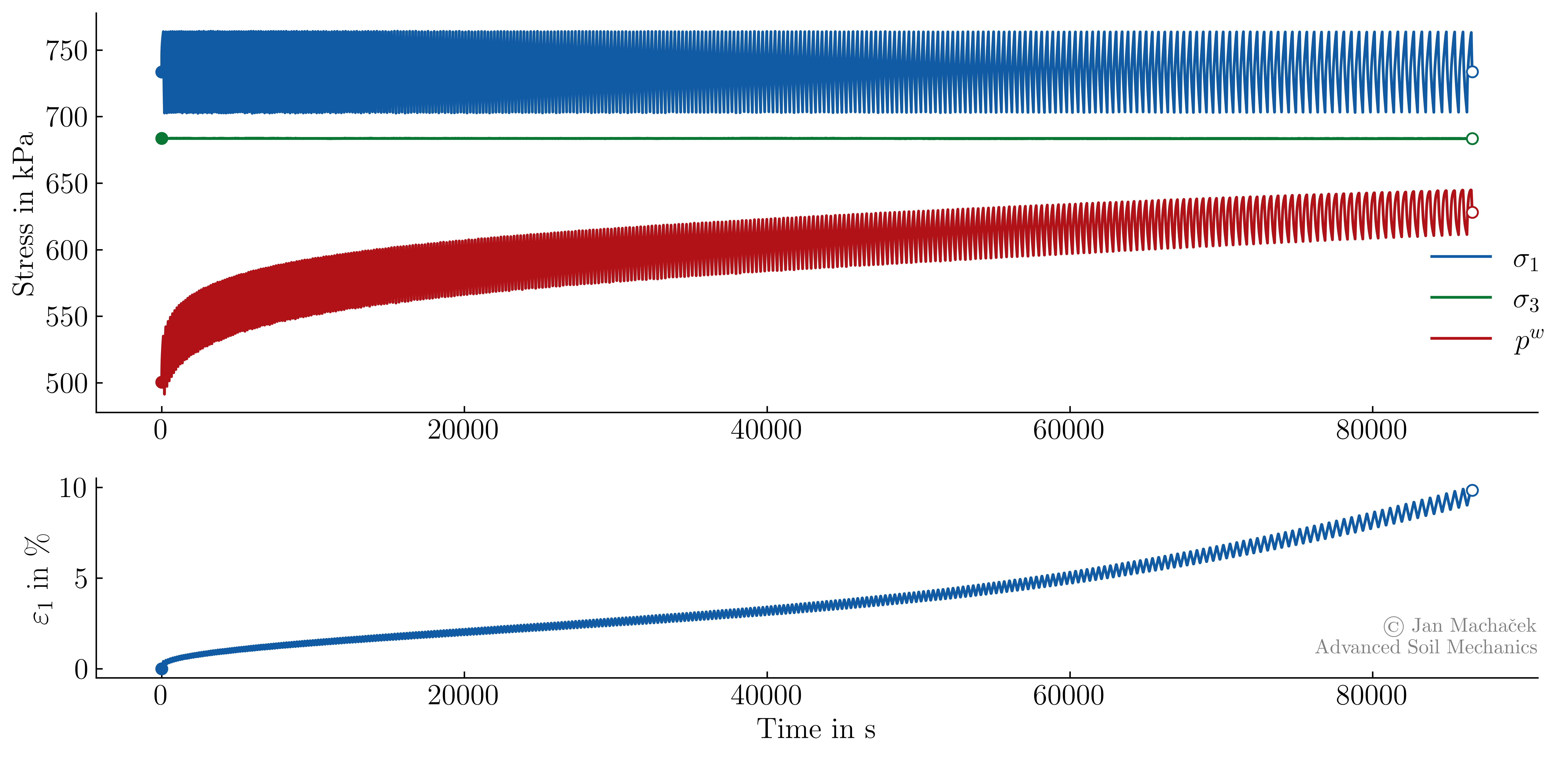
Development of (total) stresses $\sigma_1$ and $\sigma_3$, pore water pressure $p^w$, and axial strain $\varepsilon_1$ during an undrained cyclic triaxial test on Kaolin starting from an anisotropic initial stress state.

From the above figure, it can be seen that after a certain number of cycles, the accumulated pore pressure nearly stabilizes at $p^w \approx 625$ kPa. However, a considerable accumulation of permanent axial strain is observed, while the axial strain amplitude remained almost constant. This contrasts with the behavior under isotropic stress conditions, where a significant increase in axial strain amplitude is observed, while the mean axial strain remains nearly constant. The accumulation of strain continues even after pore pressure accumulation ceases. Such dependence of the failure mode on the initial stress ratio is observed in many fine-grained soils and aligns with literature findings. The corresponding stress- and strain-paths are illustrated in the figure below.

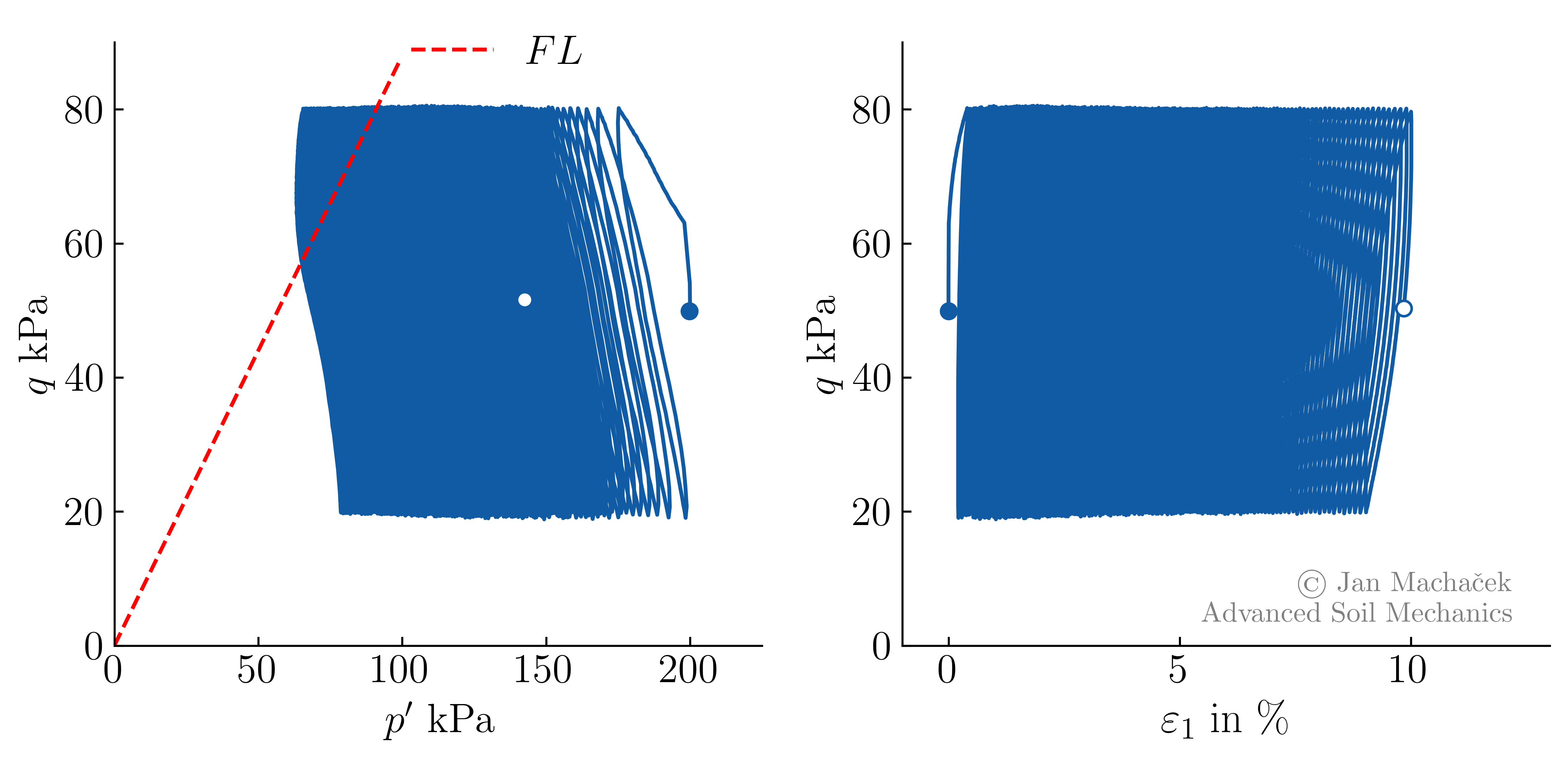
Undrained cyclic triaxial test on normally consolidated Kaolin starting from an anisotropic initial stress state: deviatoric stress $q$ over mean effective pressure $p^\prime$ (left) and over axial strain $\varepsilon_1$ (right), FL = Failure Line from monotonic tests.

The stress path in the $p^\prime-q$ plane is similar to that observed for sand under anisotropic initial stress states. Once the effective stress path reaches the failure line and after the pore water pressure stabilizes (see development of $p^w$ over time), it becomes lens-shaped.

Failure of plastic fine-grained soils under undrained cyclic loading

For medium-plastic fine-grained soils, failure under undrained cyclic shearing is not defined by vanishing mean effective pressure ($p^\prime=0$ kPa) but by:

Excessive strain amplitudes under isotropic initial stress conditions
Accumulation of strains under anisotropic initial stress conditions

Similar to sand (although not shown in the above discussion):

An increase in $p^\prime$ at constant $q^{ampl}$ and OCR leads to an increase in the number of cycles needed until failure.
With increasing OCR at constant $p^\prime$ and $q^{ampl}$, more loading cycles can be applied until failure.

Note that there may be pronounced effects of inherent (structural) anisotropy or viscosity (rate effects), particularly in clays. These were not dealt with in the previous discussion, but should generally be analysed.

Cyclic stress ratio

In the previous sections we have seen the influence of soil density, stress amplitude, mean effective pressure and stress anisotropy on the soil behaviour under undrained cyclic loading. For practical purposes however, a more condensed representation is beneficial.

For this purpose first the (triaxial) cyclic stress ratio $CSR$ is introduced as the ratio between the shear stress amplitude $q^{ampl}$ and the initial mean effective pressure $p_0^\prime$:

\[ CSR = \dfrac{q^{ampl}}{2p_0^\prime} \]

The factor 2 accounts for the definition of $q^{ampl}$ being the "double amplitude", i.e. the distance between the maximum and minimum deviatoric stress in one loading cycle. CSR combines the effect of the stress amplitude and mean effective pressure.

In order to further condense the amount of information and allow for compare different tests more easily we reduce the information about the development of stress and strain visible e.g. in the $p^\prime-q$ or $\varepsilon_1-q$ planes to one single value: the number of cycles required to reach liquefaction (or failure in general) $N_{ini}$. To evaluate $N_{ini}$, two failure criteria are often used:

The time of initial liquefaction ($p^\prime = 0$)
The time when a certain axial strain amplitude $\varepsilon_1^{ampl}$ is reached, e.g. $\varepsilon_1^{ampl} = 10$ %. Similar to $q^{ampl}$, $\varepsilon_1^{ampl}$ is calculated as the distance between the minimum and maximum axial strain in one loading cycle.

Sand

In the following example, the strain criterion has been used to evaluate a test on medium dense sand. This is shown graphically in the following figure. First, the cycle in which the strain criterion is first violated is identified. This cycle corresponds to the number of cycles to reach liquefaction $N_{ini}$, in this case it is cycle no. 144. The stress ratio is obtained from the test conditions at 0.1. This pair of values is entered into the figure on the right-hand side, which plots the stress amplitude ratio over the number of cycles to liquefaction.

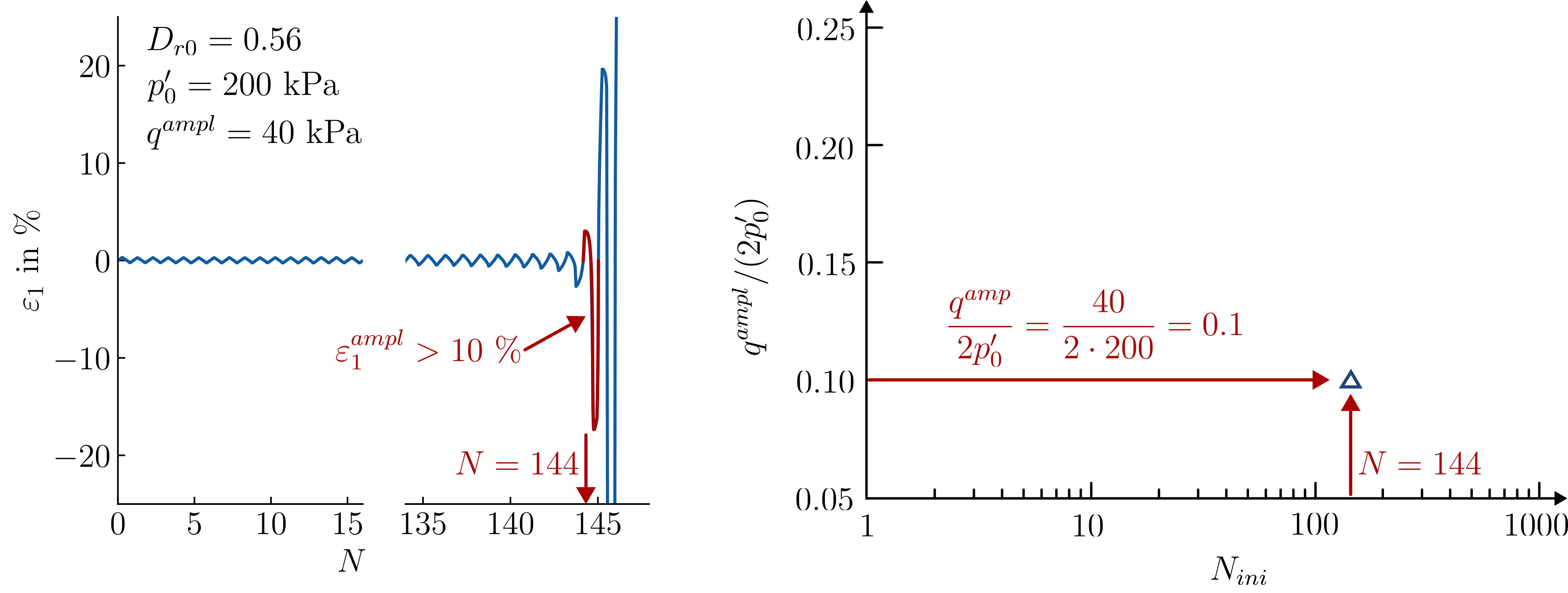Left: Axial stress over number of cycles, Right: Amplitude-stress ratio versus number of cycles to initial liquefaction

Let us now consider a series of tests on medium dense sand samples but with different initial mean effective pressures and stress amplitudes. From previous discussions in Sessions XX and YY we know that:

An increase in $p_0^\prime$ for given $D_{r0}$ and $q^{ampl}$ increases the number of cycles to initial liquefaction
An increase in $q^{ampl}$ for given $D_{r0}$ and $p_0^\prime$ decreases the number of cycles to initial liquefaction

In ¹ a series of 10 undrained cyclic triaxial tests on medium dense sand with varying $p_0^\prime$ and $q^{ampl}$ has been performed. Plotting the results in terms of $CSR$ over $N_{ini}$ yields the following:

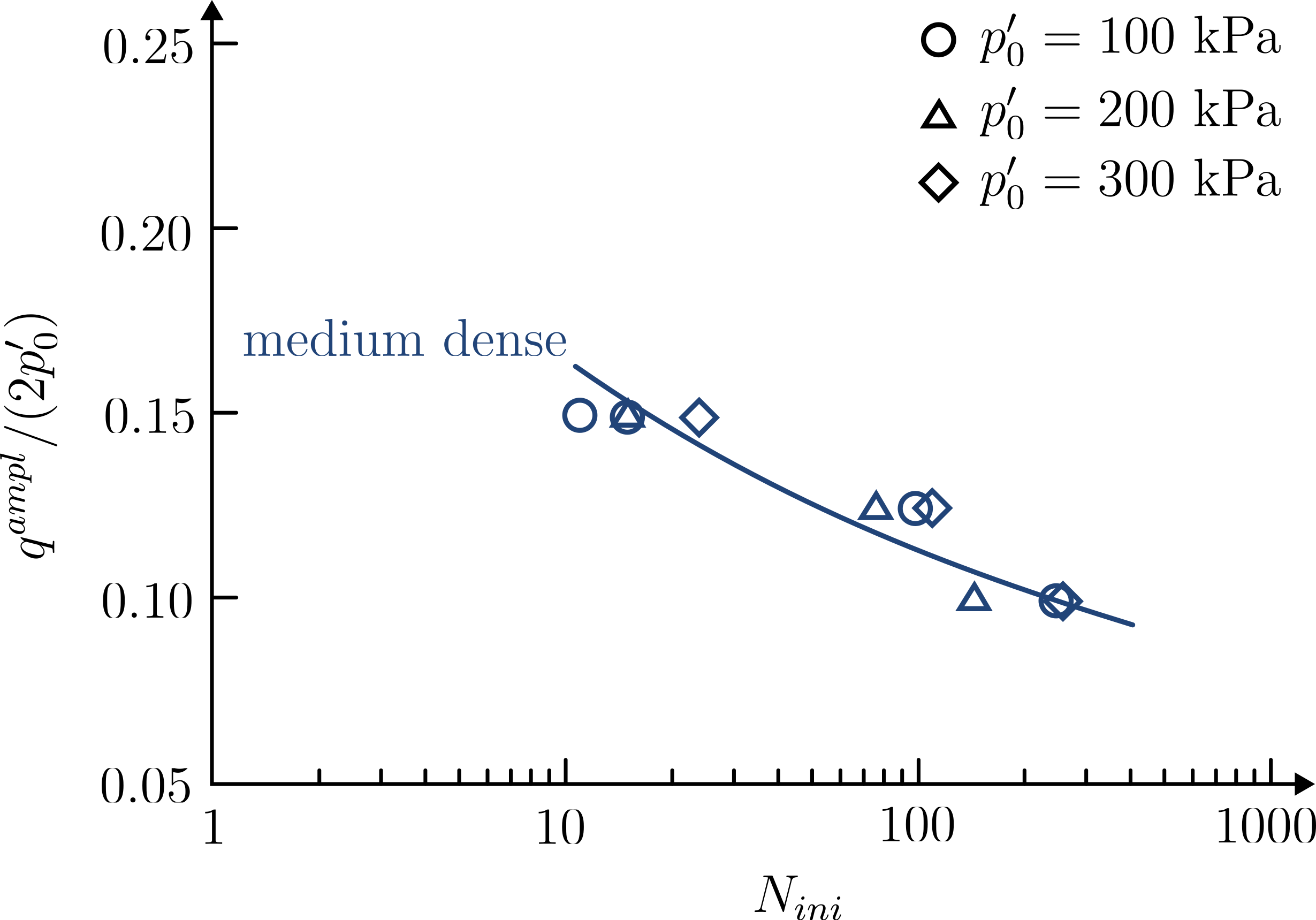
Amplitude-stress ratio versus number of cycles to initial liquefaction from 10 undrained cyclic triaxial tests on medium dense Karlsruhe Finesand

From the above figure we can see that the number of cycles to liquefaction $N_{ini}$ decreases as the CSR increases. The increase in CSR can have two causes: Either the mean effective pressure $p^\prime$ decreases or the amplitude of the shear stress $q^{ampl}$ increases. It can also be seen, that a (non-linear) relationship between CSR and $N_{ini}$ is apparent. Additional test series on loose and dense sand samples show similar behaviour. Compared to the medium dense sand, loose sand can withstand less cycles until liquefaction for the same CSR. Analogously, for the same CSR, dense sand can be subjected to more loading cycles before liquefaction occurs. This is shown in the figure below.

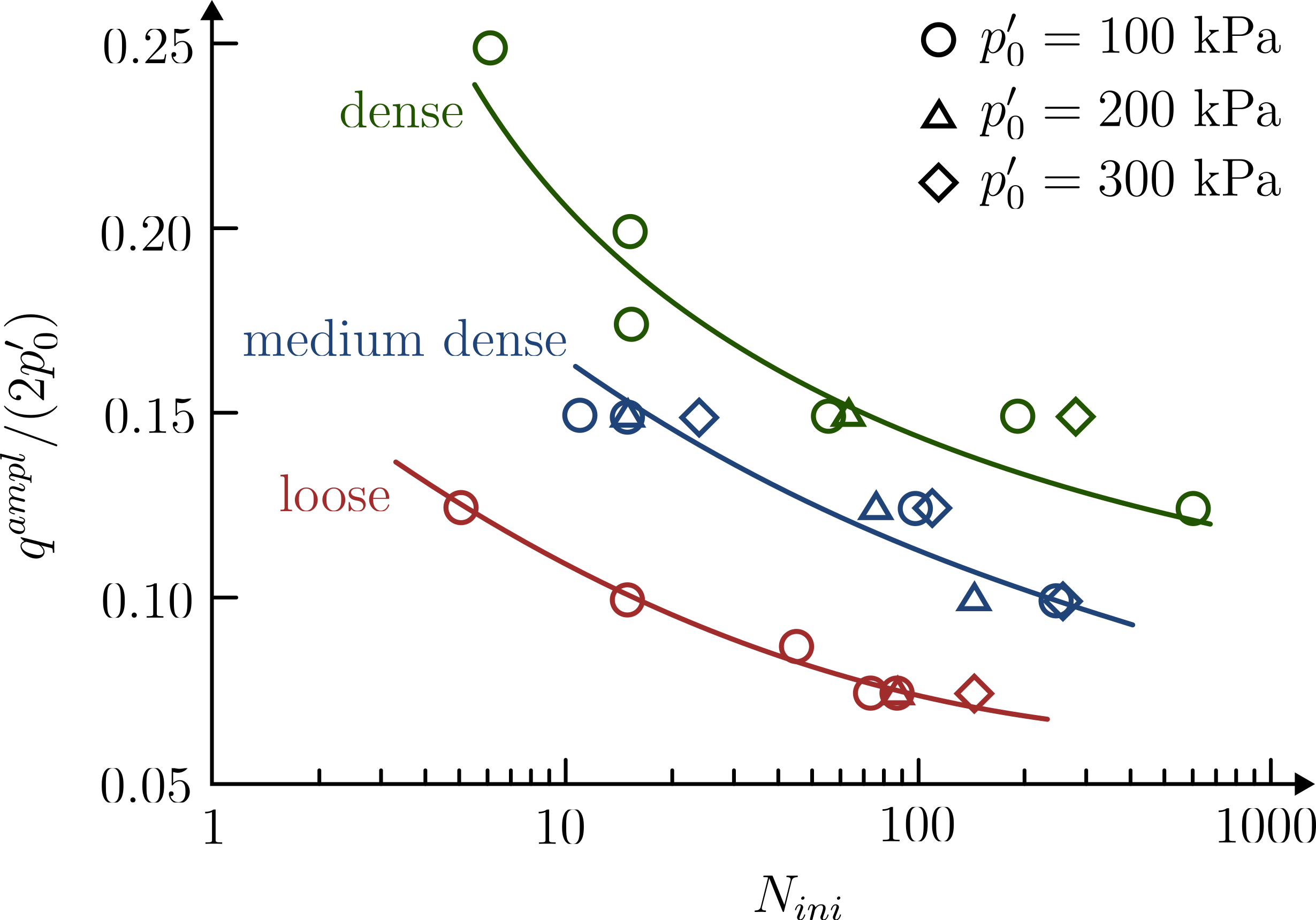
Amplitude-stress ratio versus number of cycles to initial liquefaction from undrained cyclic triaxial tests on loose, medium dense and dense Karlsruhe Finesand

Fine-grained soils

The same approach of condensing the amount of information can be applied to the results obtained for fine-grained soils. Contrary to sand, only the second method of evaluating $N_{ini}$ can be applied to plastic fine-grained soils as liquefaction $p^\prime=0$ is not reached. An examplary CSR-$N_{ini}$ graph obtained from 14 undrained cyclic triaxial tests on Kaolin ² is given in below figure. As for sand, with increasing amplitude-stress ratio CSR a decrease in $N_{ini}$ is observed.

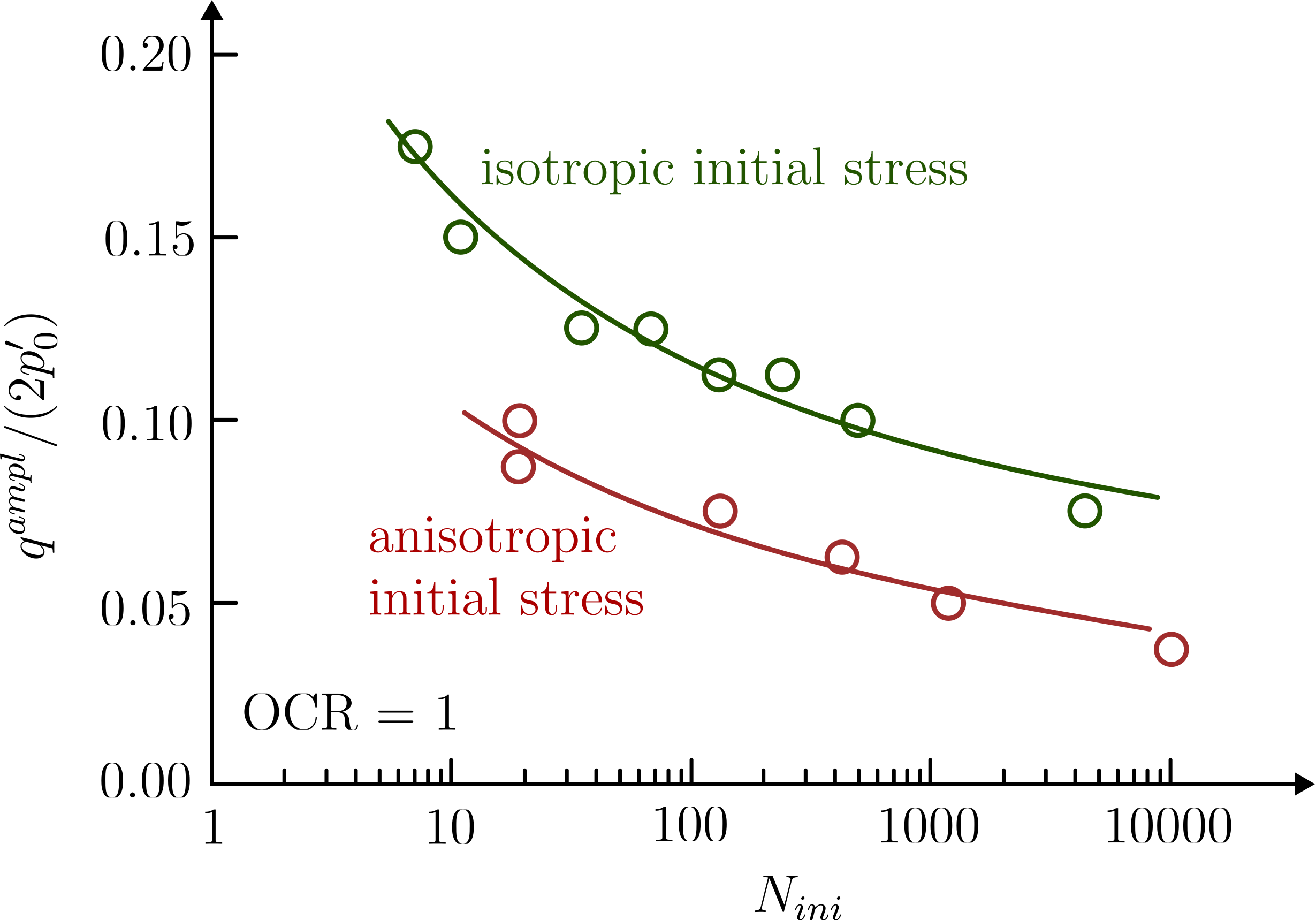
Amplitude-stress ratio versus number of cycles to initial liquefaction from undrained cyclic triaxial tests on normally consolidated Kaolin

T. Wichtmann and T. Triantafyllidis, ‘An experimental database for the development, calibration and verification of constitutive models for sand with focus to cyclic loading: part I—tests with monotonic loading and stress cycles’, Acta Geotech., vol. 11, no. 4, pp. 739–761, Aug. 2016, doi: 10.1007/s11440-015-0402-z. ↩
T. Wichtmann and T. Triantafyllidis, ‘Monotonic and cyclic tests on kaolin: a database for the development, calibration and verification of constitutive models for cohesive soils with focus to cyclic loading’, Acta Geotech., vol. 13, no. 5, pp. 1103–1128, Oct. 2018, doi: 10.1007/s11440-017-0588-3. ↩↩