Basic Concepts of the Theory of Porous Media

When modelling saturated soils, it is not sufficient to consider the solid skeleton alone. The pore fluid - typically water - interacts continuously with the solid matrix, influencing and being influenced by mechanical deformation, pore structure, and permeability. The Theory of Porous Media (TPM) provides a rigorous continuum-mechanical framework to represent these coupled processes. It models the material as a mixture of distinct constituents (solid and fluid phases), each occupying the same spatial location but retaining independent kinematics and constitutive behaviour.

In doing so, TPM adopts a macroscopic, averaged view of the porous medium. The following assumptions form the basis of the theory:

All constituents are in a state of ideal disarrangement - they coexist at every point without forming identifiable geometric patterns or preferred orientations.
Each phase is statistically distributed over the control space, which means that its presence is not tracked at the microscopic scale.
All physical quantities (e.g. stress, density, velocity) are interpreted as statistical averages over a representative elementary volume (REV), not as values at individual particles or pores.
As a consequence, no geometrically exact representation of the pore structure is included.
The model contains no information about the exact location of individual phases at the microscale.

While these assumptions limit the spatial resolution of the description, they allow the derivation of well-posed field equations and enable the application of the finite element method. In practice, the macroscopic viewpoint of TPM is sufficiently accurate for most engineering problems involving saturated soils.

TPM generalises and unifies various concepts already encountered in undergraduate soil mechanics, such as the use of volume fractions to estimate saturated density and Darcy’s law for pore fluid flow. It also provides a systematic approach to derive the governing equations for mass and momentum balance. These balance laws, together with suitable constitutive models, form the basis of numerical simulations of saturated (and later unsaturated) soils.

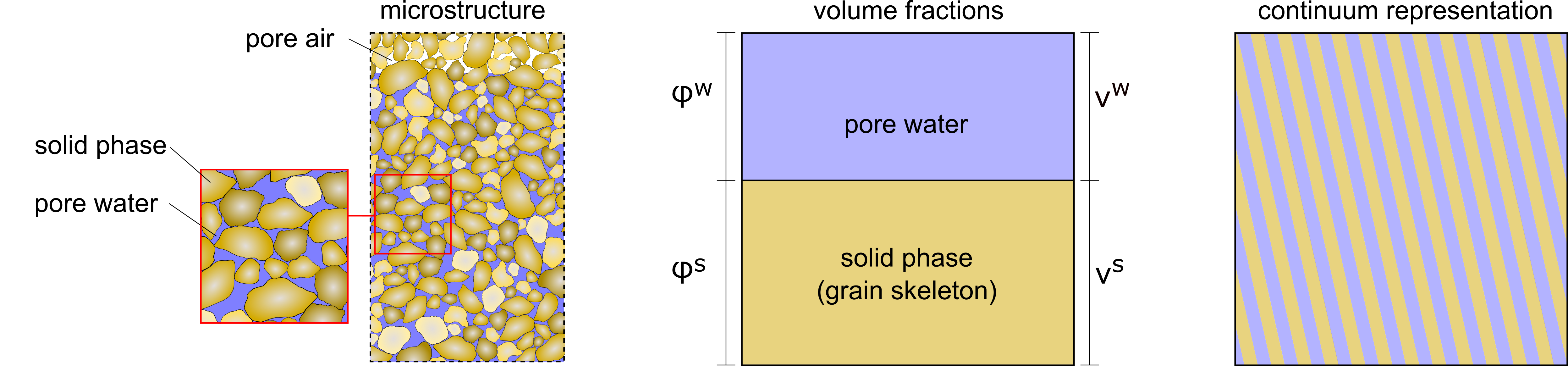Figure 1: Different representations of a saturated soil. Left: microscopic view, centre: schematic of volume fractions, right: macroscopic continuum.

Figure 1 illustrates three representations of saturated soil. On the left is the grain-scale structure, where solid particles are in contact and the voids are filled with water. In the middle, the same system is idealised as a combination of volume fractions. On the right, the material is represented as a continuum, which is the level at which numerical modelling takes place. TPM bridges the microscopic physics and the continuum formulation by quantifying how much of the total volume is occupied by each phase.

Concept of Volume Fractions

The local composition of a porous medium is described using volume fractions:

\[ \varphi^\alpha = \frac{\text{d} V^\alpha}{\text{d} V}, \]

where \(\text{d} V^\alpha\) is the volume occupied by phase \(\alpha\) (solid or fluid), and \(\text{d} V\) is the total volume of the mixture. The sum of the partial volumes gives the total volume:

\[ \text{d} V = \sum_\alpha \text{d} V^\alpha, \]

which implies the constraint:

\[ \sum_\alpha \varphi^\alpha = 1. \]

This ensures that all phases together completely fill the space at each material point.

The volume fraction formalism is already familiar from undergraduate soil mechanics, for example in the computation of the saturated unit weight \(\gamma_{\text{sat}}\), where the total density is obtained by weighting the densities of the solid and fluid phases based on their volumetric contribution.

To relate physical quantities, such as density or mass, to the volume they are defined over, we distinguish between:

Intrinsic quantities \(\bar{\sqcup}^\alpha\): defined per unit volume of phase \(\alpha\)
Partial quantities \(\sqcup^\alpha\): defined per unit volume of the mixture

These are related by:

\[ \sqcup^\alpha = \varphi^\alpha \bar{\sqcup}^\alpha. \]

Applying this to mass density yields the partial density of a phase:

\[ \rho^\alpha = \varphi^\alpha \bar{\rho}^\alpha, \]

and the total density of the mixture becomes:

\[ \rho^{\text{tot}} = \sum_\alpha \rho^\alpha = \sum_\alpha \varphi^\alpha \bar{\rho}^\alpha. \]

In the case of a saturated two-phase system consisting of solid and water, this reduces to:

\[ \rho^{\text{tot}} = \varphi^s \bar{\rho}^s + \varphi^w \bar{\rho}^w. \]

We now introduce the porosity \(n\), which describes the fraction of the total volume not occupied by solids:

\[ n = 1 - \varphi^s = \varphi^w. \]

This gives the well-known expression for the total density of a saturated soil:

\[ \rho^{\text{tot}} = (1 - n) \bar{\rho}^s + n \bar{\rho}^w. \]

Porosity has a clear physical meaning: it tells us how much of the material consists of void space, and for saturated conditions, how much of that space is filled with water. It plays a central role in defining transport and deformation properties.

Kinematic Relations

The Theory of Porous Media treats each phase—solid and fluid—as a fully interpenetrating continuum. At any point in space and time, multiple constituents may coexist, each with its own kinematic description. The model assumes:

Each phase has a well-defined and continuous motion.
No phase occupies the entire control volume alone; they are superimposed and idealised as coexisting continua.

This means that every constituent α (solid or fluid) has its own function of motion:

\[ x_i = x_i^\alpha(X_i^\alpha, t), \]

where \(X_i^\alpha\) denotes the reference (undeformed) position of the material point belonging to phase \(\alpha\), and \(x_i\) is its current spatial position at time \(t\). As illustrated in Figure 2, each phase in the mixture is assumed to follow its own motion. That means that at any spatial location \(x_i\) and time \(t\), there may be particles from different phases occupying the same position.

Figure 2: Motion functions \(x_i^\alpha(X_i^\alpha, t)\) for different phases \(\alpha\) of the porous medium.

Differentiating the motion function with respect to time yields the intrinsic velocity and acceleration of the phase:

\[ \bar{v}_i^\alpha = \frac{\text{d} x_i^\alpha}{\text{d} t}, \qquad \bar{a}_i^\alpha = \frac{\text{d}^2 x_i^\alpha}{\text{d} t^2}. \]

To describe how scalar fields \(\sqcup\) - such as pressure \(p^\alpha\) or density \(\rho^\alpha\) - change for a given phase, the material derivative is introduced:

\[ \frac{\text{d}^\alpha \sqcup}{\text{d} t} = \frac{\partial \sqcup}{\partial t} + \bar{v}_i^\alpha \frac{\partial \sqcup}{\partial x_i}. \]

This total time derivative captures two effects:

A local change: how the quantity \(\sqcup\) varies at a fixed point in space over time.
A convective change: how the value changes as the material point moves through space and experiences different values of \(\sqcup\) in a non-uniform field.

In the context of finite element modelling, we typically adopt a Lagrangian description for the solid phase. That is, the mesh moves with the solid skeleton, and the displacements \(\bar{u}_i^s = \bar{x}_i^s - \bar{X}_i^s\) are directly tracked at the element nodes. This is feasible because the motion of the solid is generally small and smooth.

However, the situation is different for the pore water. Fluid velocities are often significantly higher than those of the solid - especially in cases of infiltration or drainage. If we were to track water motion in a purely Lagrangian way, the mesh would undergo extreme distortions, making the finite element computation unstable or even impossible. Therefore, we use a relative (quasi-Eulerian) description for the fluid motion: the pore water motion is followed relative to the deforming solid skeleton.

This leads to the seepage velocity:

\[ \bar{w}_i^\beta = \bar{v}_i^\beta - \bar{v}_i^s, \]

which describes the velocity of fluid phase \(\beta\) (e.g. water) relative to the solid. Using this, the material derivative for any scalar field \(\sqcup\) carried by the fluid can be reformulated in terms of the solid motion:

\[ \frac{\text{d}^\beta \sqcup}{\text{d} t} = \frac{\text{d}^s \sqcup}{\text{d} t} + \bar{w}_i^\beta \frac{\partial \sqcup}{\partial x_i}. \]

This expression combines the time derivative following the solid phase with the convective change due to the relative fluid motion.

We also define the Darcy velocity \(w_i^\beta\), which represents the volumetric discharge of the fluid phase \(\beta\) through a unit area of the mixture:

\[ w_i^\beta = \varphi^\beta \bar{w}_i^\beta = \varphi^\beta (\bar{v}_i^\beta - \bar{v}_i^s). \]

This quantity generalises the Darcy law known from undergraduate soil mechanics, where the flow rate is proportional to the pressure gradient. In the TPM framework, Darcy’s law will later appear as a constitutive relationship derived from the balance of linear momentum for the fluid phase, rather than being introduced phenomenologically.

The kinematic framework introduced here forms the basis for expressing the balance equations in a mixture theory setting. It allows the solid and fluid phases to be coupled naturally, each with appropriate reference frames for numerical implementation. In the next section, we use these kinematic relations to formulate the mass balance equation for the pore water.