Skip to content

Stress and strain

When we examine many types of soils, we find that they are granular materials, comprised of an immensely large number of particles. In the case of sands, these particles form what we often refer to as a grain skeleton. Conversely, clays consist of microscopic plate-like particles that tend to align and overlap, forming aggregates. These aggregates, however, form structures that are similar to the grain skeleton of granular materials. Forces acting on this grain structure, whether from the grains' own weight or from an externally applied load, are transmitted through grain-to-grain contacts at the points where the grains meet.

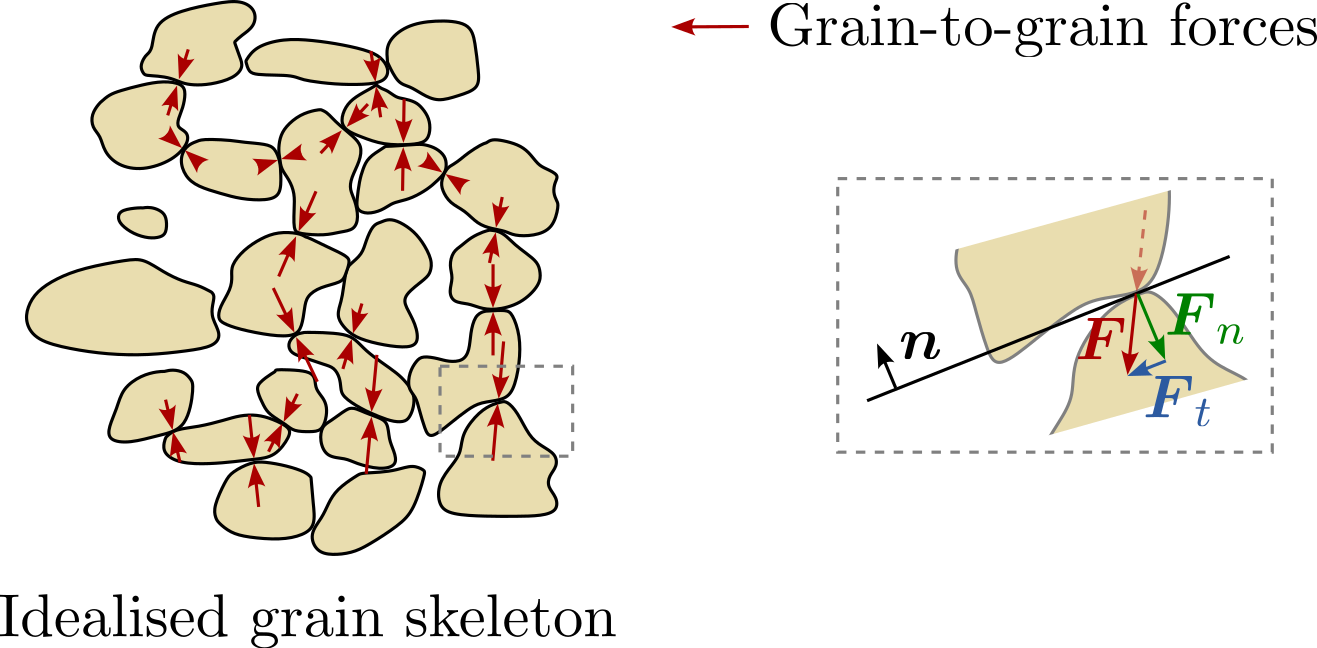
grain-to-grain-forces
Simplified representation of a grain skeleton and grain-to-grain forces.

A sequence of particles (grains) through which forces are transmitted is referred to as a 'force chain'. Within granular materials like sand, not all particles bear the same amount of force. Instead, forces often concentrate along certain paths or chains of particles, creating these force chains. These chains can be visualized as lines or paths of higher stress passing through the material, effectively transferring the applied force through a series of grains. An example of 'force chains' resulting from the soils dead weight is given in below figure showing the results of a Discrete Element simulation of a loosely pluviated cone of sand performed by Nadukuru & Michalowski1.

force-chains Discrete Element simulation from 1: (top) prismatic sand heap, (bottom) force chains.

Directly modeling grain-to-grain forces and force chains in granular materials presents significant challenges due to the immense computational capacities required and the difficulties in abstracting individual particle interactions at larger scales. Consequently, like in most engineering disciplines, the concept of stress from continuum mechanics is often employed.

In the context of granular media, such as soils, this stress represents an averaged measure of the contact forces between grains over a representative volume. Thus, the intricate details of force chains are encompassed within a continuous and differentiable stress field, which provides both the magnitude and orientation of the averaged contact forces.

Stress is a physical quantity that cannot be represented by a single scalar value. Instead, the state of stress is defined at a specific point within a material. At this point, numerous planes or directions can be considered. To describe the stress state comprehensively, a coordinate system (often denoted as \(x, y, z\)) is required, along with six independent tensor components2:

\[ \boldsymbol{\sigma} = \begin{bmatrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \end{bmatrix} ~~~\text{where:}~~~ \sigma_{xy}=\sigma_{yx}~~~,~~~\sigma_{xz}=\sigma_{zx}~~~,~~~\sigma_{yz}=\sigma_{zy} \]

A more detailed treatment of the stress tensor can be found in Section Stress tensor and its Invariants. However, it is recommended to first study the chapter on the Notation used (and some calculation rules).

  1. S. S. Nadukuru and R. L. Michalowski, ‘Arching in Distribution of Active Load on Retaining Walls’, J. Geotech. Geoenviron. Eng., vol. 138, no. 5, pp. 575–584, May 2012, doi: 10.1061/(ASCE)GT.1943-5606.0000617. ↩

  2. D. Kolymbas, Geotechnik: Bodenmechanik, Grundbau und Tunnelbau. Berlin, Heidelberg: Springer Berlin Heidelberg, 2011. ↩