Skip to content

Effective stress in partially saturated soils

The effective stress concept for saturated soils has been introduced in section Effective stress. From the considerations in the previous section it becomes clear, that additional forces need to be taken into account for the calculation of the effective stress (grain-to-grain forces) in partially saturated soils. Various "effective" stresses have also been proposed for unsaturated soils in a form similar to the one for saturated soils

\[ \sigma_{ij}^\prime = \sigma_{ij} - \chi s 1_{ij} \]

where \(s=p^a-p^w\) is the suction and \(\chi(S)\) an empirical factor depending on the degree of saturation \(S\). The primary objective is to find a definition of effective stress which allows to describe strength and stiffness of partially saturated soils as observed in laboratory tests. However, so far no scalar function \(\chi(S)\) was proposed that satisfactorily fulfils this objective.

Bishop effective stress

The relationship most often mentioned in this context is the so-called Bishop's stress. Although it is not a sufficient basis for describing the soil behaviour observed in laboratory experiments, we will discuss it in detail in the lecture. The reason for this is that it is the basis of all available computer programs for simulating partially saturated soils.

To derive the Bishop effective stress, we consider the idealised representation of two soil grains as spheres, as shown in Figure 1.


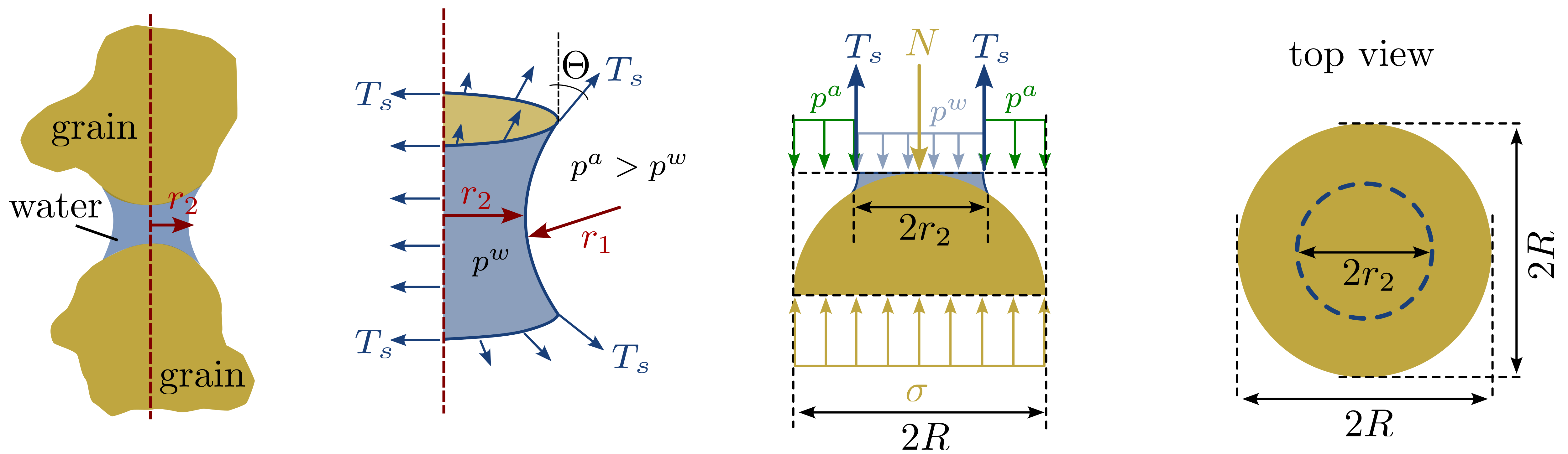
Figure 1. Idealised representation of two soil particles in the capillary zone being in contact with water

In above illustration, the radii of curvature are labelled \(r_1\) and \(r_2\), while the radius of a grain is labelled \(R\). \(N\) are the grain-to-grain (effective) forces in normal direction, \(\sigma\) is the total stress. From this representation, the following equilibrium of forces can be established in the vertical direction:

\[ N = \sigma \pi R^2 - p^w \pi r_2^2 - p^a (\pi R^2 - \pi r_2^2) + 2 T_s \pi r_2 \]

which reads in terms of effective stress

\[ \sigma' = \frac{N}{\pi R^2} = \sigma - p^a + (p^a - p^w)\frac{\pi r_2^2}{\pi R^2} + 2T_s\frac{\pi r_2}{\pi R^2} \]

substituting \(T_s = (p^a-p^w) \left(\dfrac{1}{r_1}+\dfrac{1}{r_2}\right)\) in above equation yields

\[ \begin{align} \sigma' &= \sigma - p^a + \left( p^a - p^w \right) \cdot \frac{\pi r_2^2}{4 R^2} + \left( p^a - p^w \right) \cdot \frac{1}{\left( \frac{1}{r_1} - \frac{1}{r_2} \right)} \cdot \frac{2 \pi r_2}{4 R^2} \nonumber \\ &= \sigma - p^a + (p^a - p^w) \cdot \underbrace{\left( \frac{\pi r_2^2}{4 R^2} \cdot \frac{r_2 + r_1}{r_2 - r_1} \right)}_{\chi} \nonumber \end{align} \]

This corresponds to the formulation of Bishop (1959) with the parameter \(\chi\):

\[ \sigma^\prime = \sigma - p^a + \chi(p^a - p^w) \]

or in 3D

\[ \sigma^\prime_{ij} = \sigma_{ij} - p^a 1_{ij} + \chi(p^a - p^w)1_{ij} \]

The difficulty in the above equation lies in determining the factor \(\chi\). As can be seen from the presented derivation, \(\chi\) performs the task of "geometrically weighting" the contribution of the suction \(s=p^a-p^w\) to the effective stress \(\sigma^\prime_{ij}\). This factor is difficult to determine for real soils, which has led to the development of various approaches to estimating \(\chi\).

The most commonly used relationship is \(\chi = S^\kappa\), where in most cases (and computer programs) \(\kappa = 1\). The advantage of linking the factor \(\chi\) to the degree of saturation \(S\) in this way is that the original formulation of effective stress is recovered at the limits:

  • for completely dry soils, \(S = 0\) and \(\chi=0\) and thus \(\sigma_{ij}^\prime = \sigma_{ij} - p^a 1_{ij}\)
  • for fully saturated soils, \(S=1\) and \(\chi=1\) and thus \(\sigma_{ij}^\prime = \sigma_{ij} + p^w 1_{ij}\)

References

  1. Kaye, G. W. C., & Laby, T. H. (1928). Tables of physical and chemical constants and some mathematical functions. Longmans, Green and Company Limited. ↩

  2. Y. Mualem, ‘A new model for predicting the hydraulic conductivity of unsaturated porous media’, Water Resources Research, vol. 12, no. 3, pp. 513–522, Jun. 1976, doi: 10.1029/wr012i003p00513. ↩

  3. M. Th. van Genuchten, ‘A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils’, Soil Science Society of America Journal, vol. 44, no. 5, pp. 892–898, Sep. 1980, doi: 10.2136/sssaj1980.03615995004400050002x. ↩