SANISAND

For the validation of the Sanisand-2 implemetations of the SANISAND constitutive model available in numgeo, a comparison with the simulation results on Toyoura Sand reported in the original paper (Dafalias & Manzari (2004)¹) is made. The Sanisand-2 implementation currently offers access to two different integration schemes:

• Modified-Euler: explicit integration scheme with adaptive time integration and error control
• Forward-Euler: explicit integration scheme wit constant substep size

Gratefully, Sheng Zeng and Mahdi Taiebat provided their implementation of the SANISAND-04. They furthermore contributed simulation results of the same tests as in [1] such that a total of three implementations could be used to benchmark the implementation in numgeo. The simulation results from Taiebat & Sheng were performed using either the finite element code OpenSees or their in-house constitutive model driver ConModel.

Input files

The input files for the benchmark simulations can be downloaded here (ME) and here (FE).

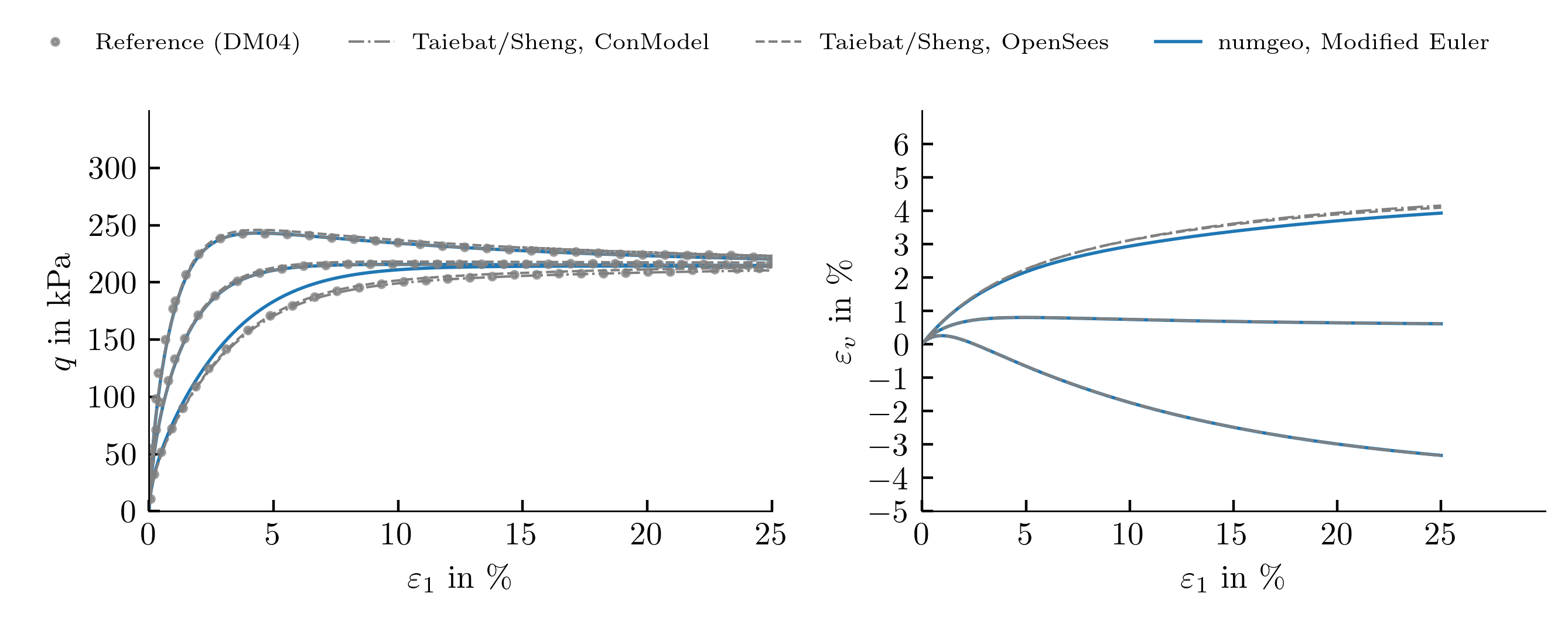
Modified Euler

Drained monotonic triaxial tests

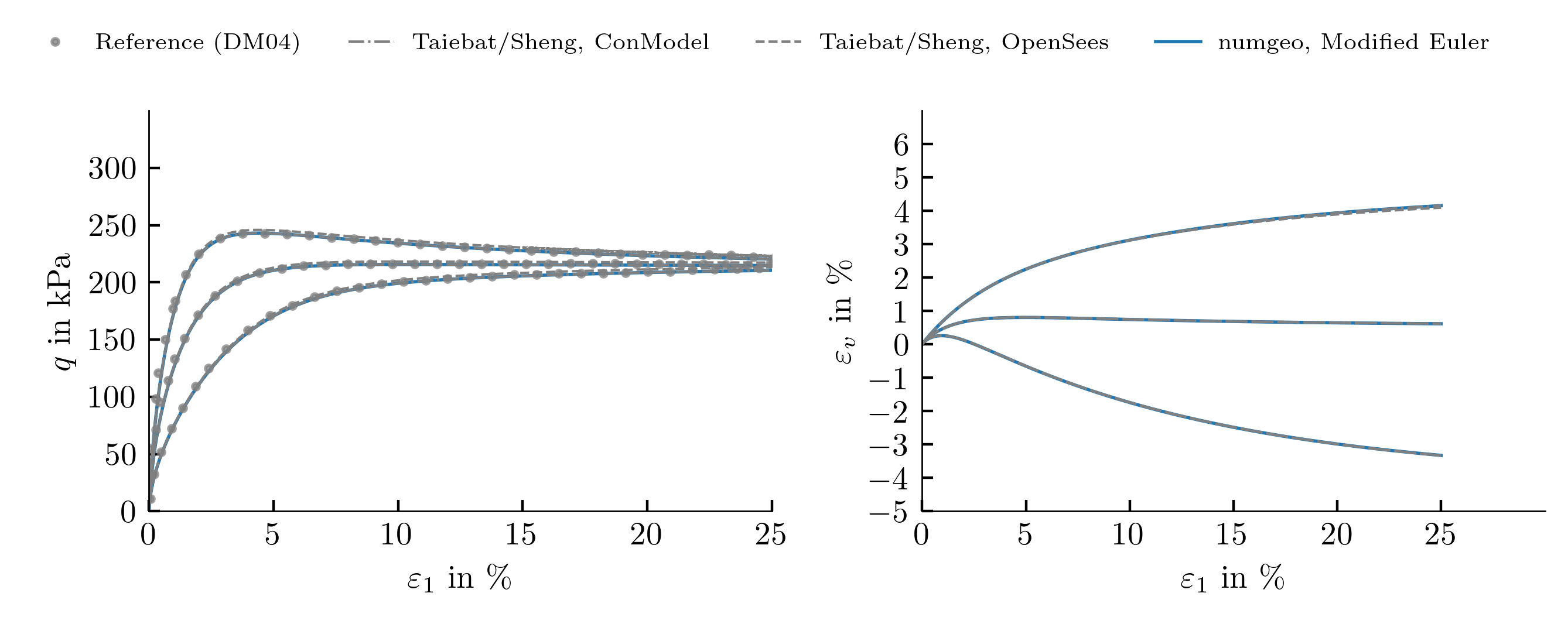
Drained monotonic triaxial tests, \(p_0=100\) kPa, \(e_0=\{0.831,0.917,0.996\}\)

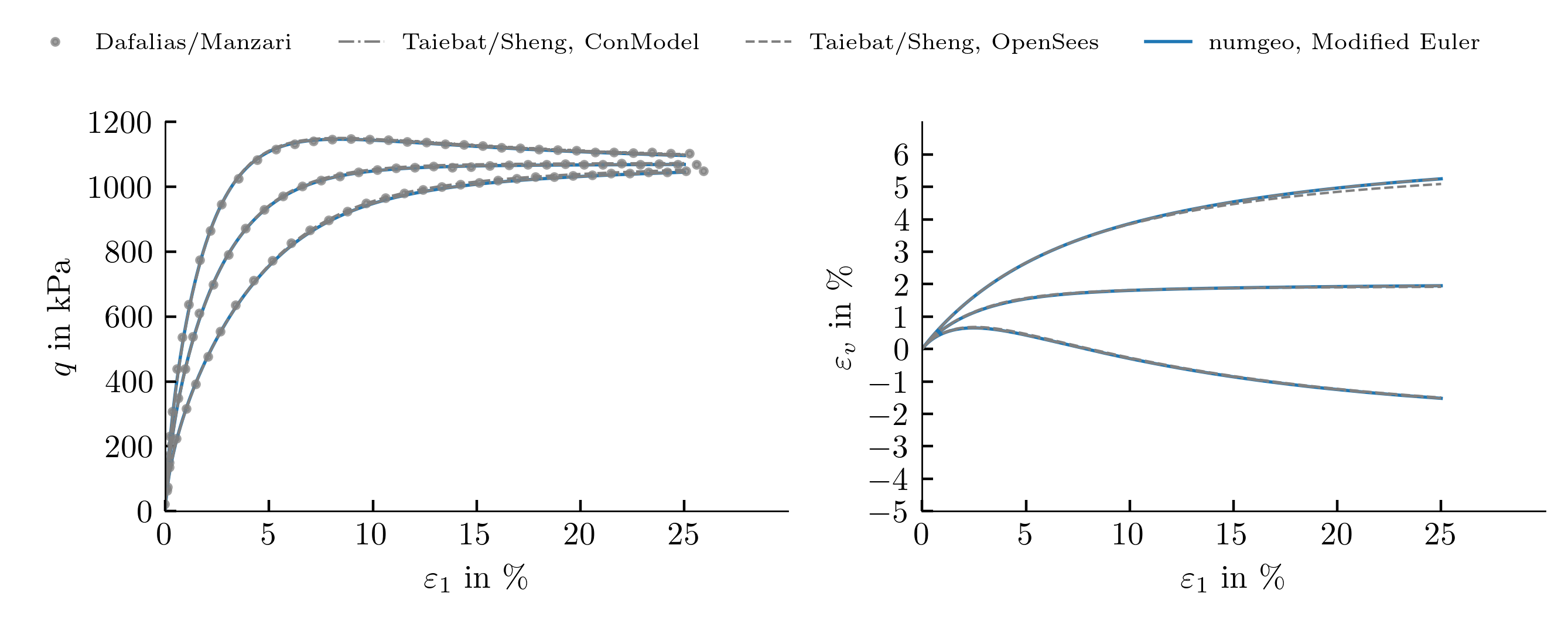
Drained monotonic triaxial tests, \(p_0=500\) kPa, \(e_0=\{0.810,0.886,0.960\}\)

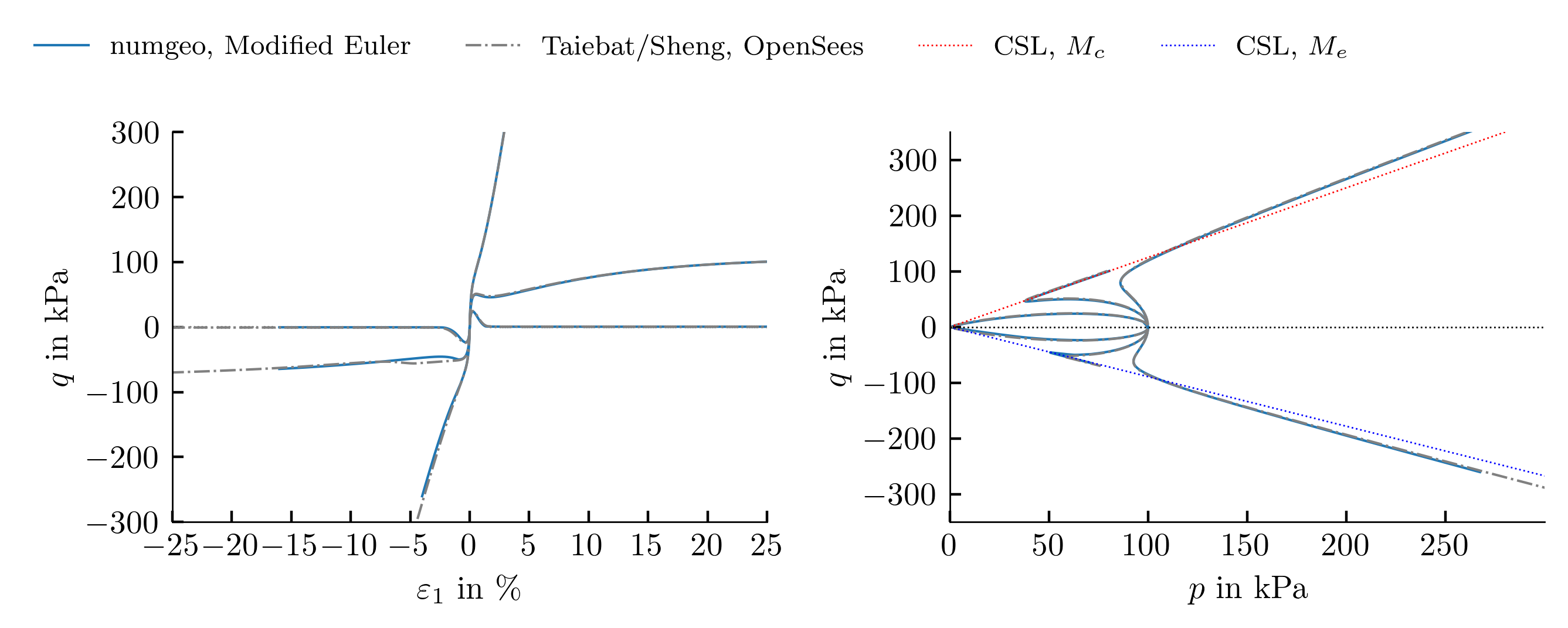
Undrained monotonic triaxial compression and extension tests

The triaxial compression and extension tests under undrained conditions studied for validation included a total of six simulations. All simulations start from an initial mean effective stress of 100 kPa. Three different initial void ratios were considered.

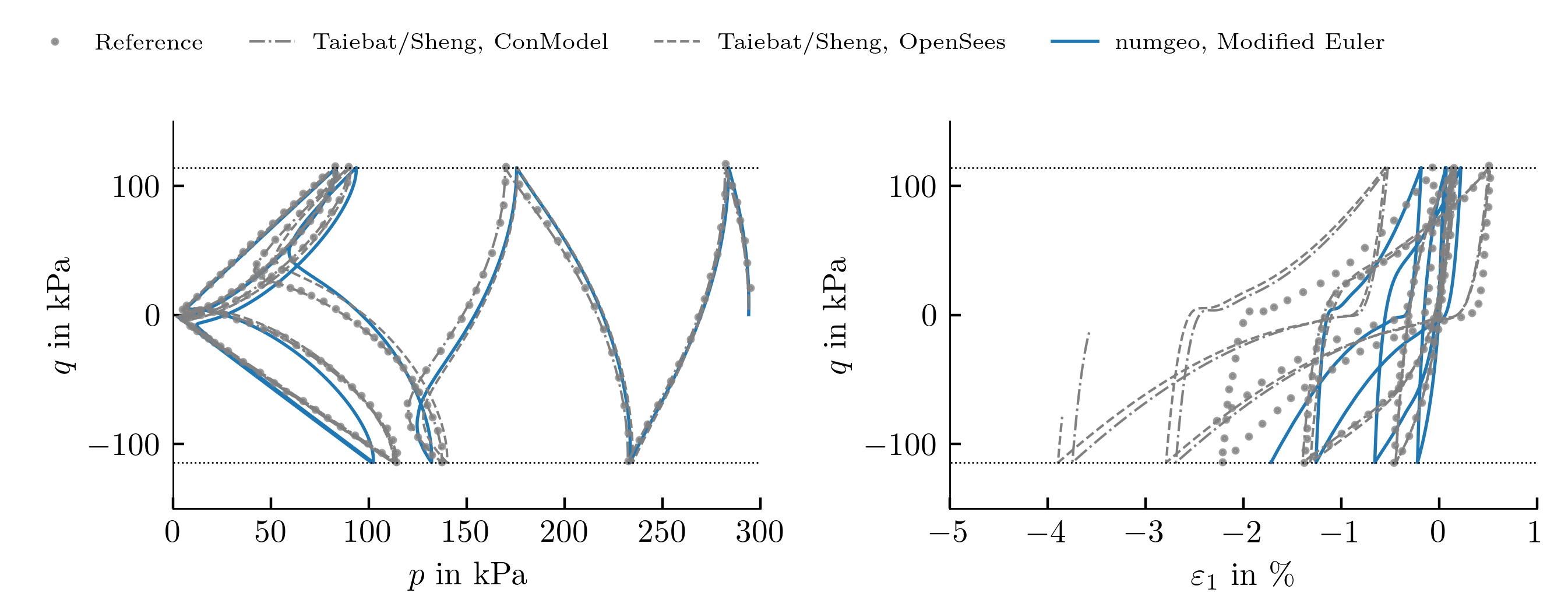
Undrained cyclic triaxial test

Forward Euler

Drained monotonic triaxial tests

Drained monotonic triaxial tests, \(p_0=100\) kPa, \(e_0=\{0.831,0.917,0.996\}\)

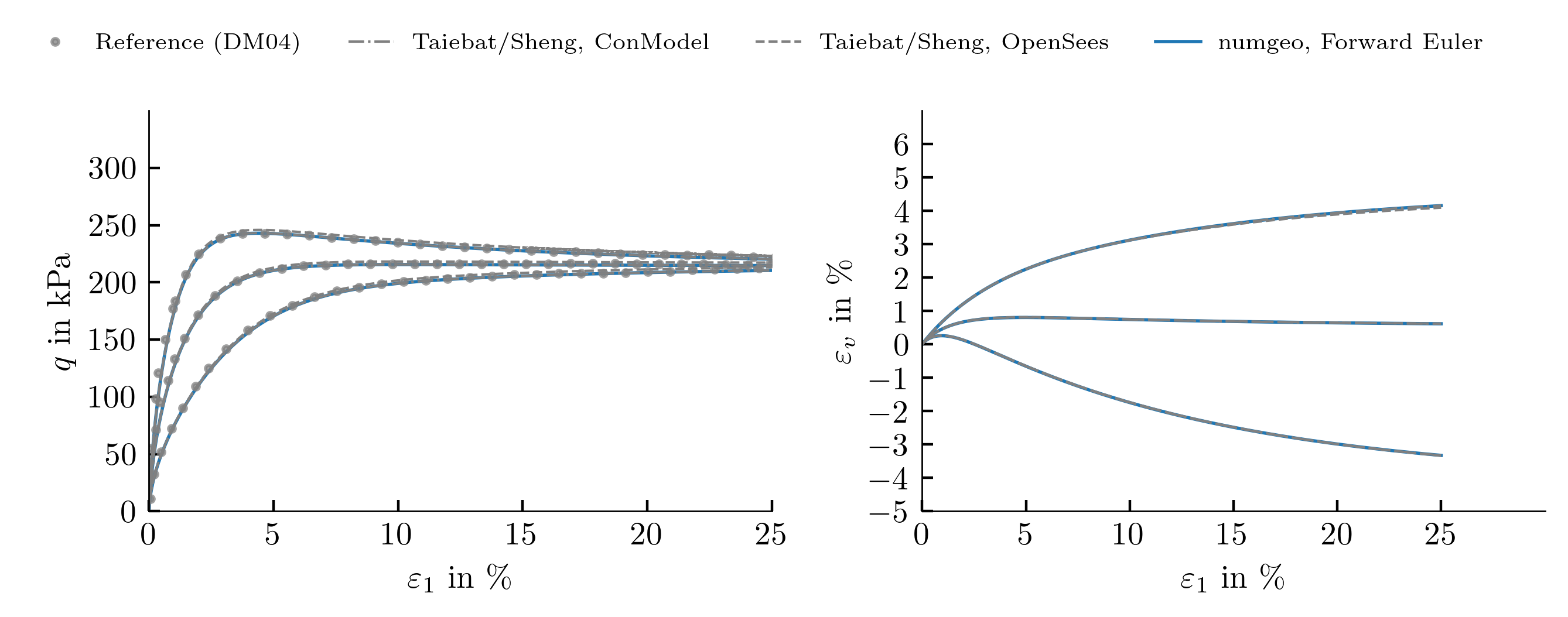
Drained monotonic triaxial tests, \(p_0=500\) kPa, \(e_0=\{0.810,0.886,0.960\}\)

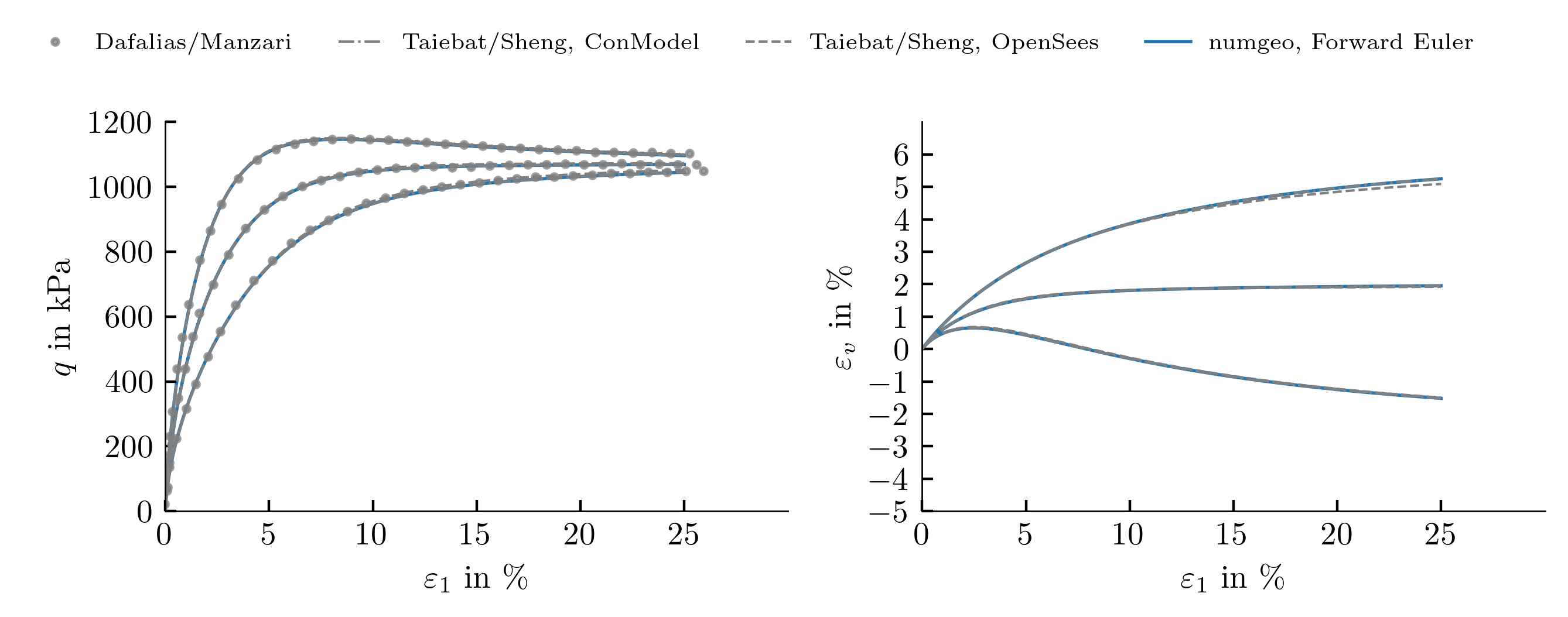
Undrained monotonic triaxial compression and extension tests

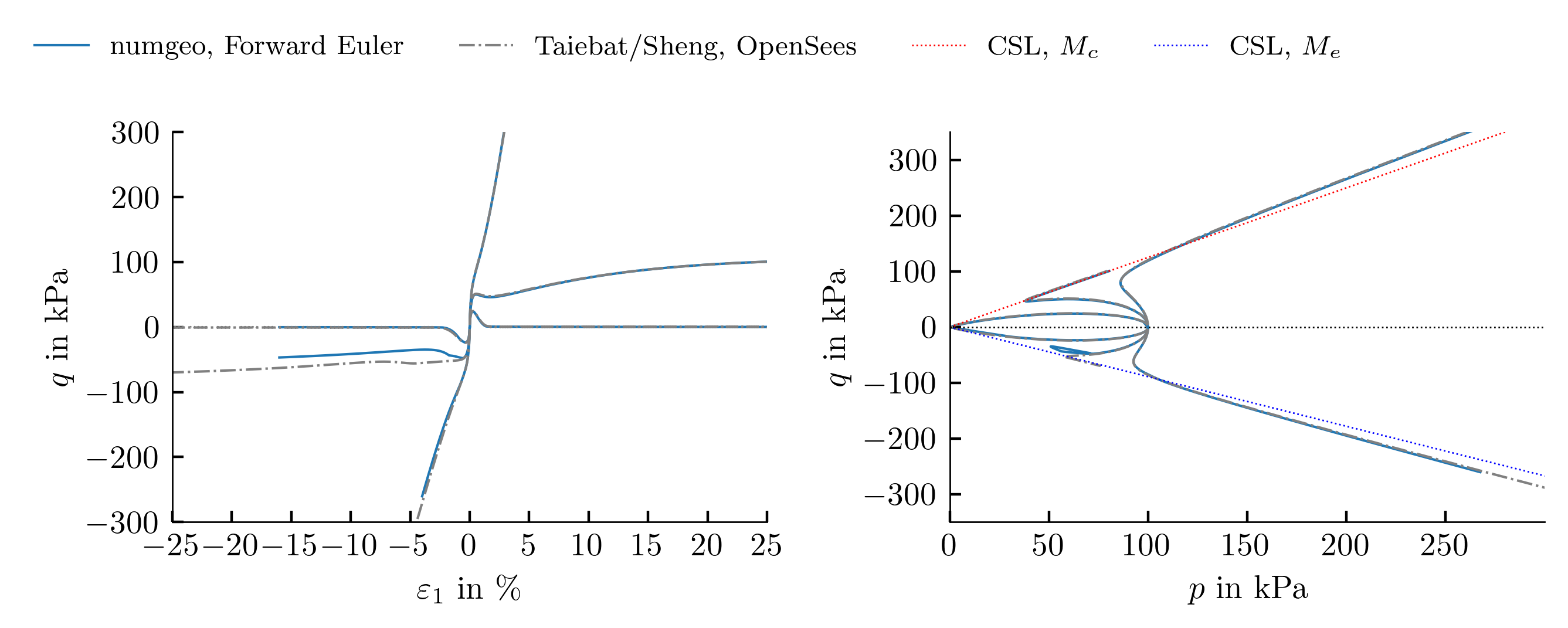
Undrained cyclic triaxial test

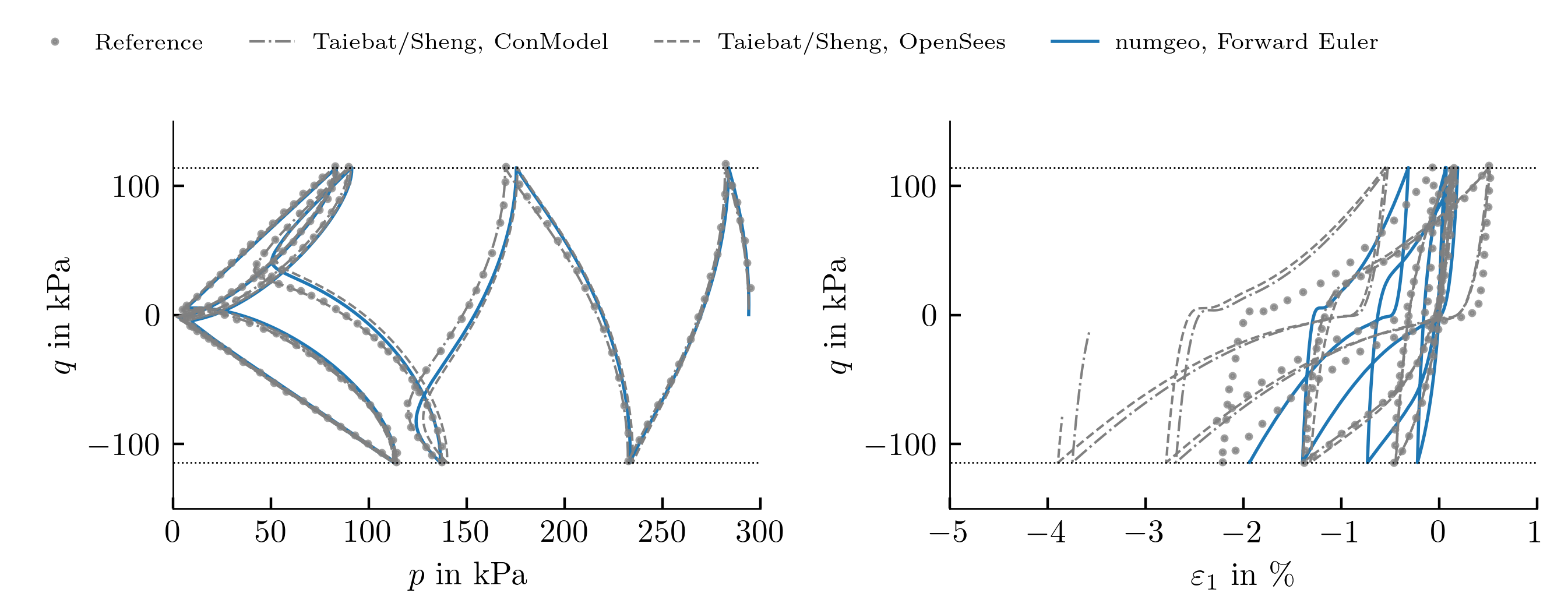
Modified formulation of \(M_b\)

In numgeo we also implement a modified formulation of the bounding surface slope \(M_b=M_c exp(n_b<-\psi>)\) instead of the original formulation \(M_b=M_c exp(-n_b \psi)\). This modification ensures that \(M_b\) cannot fall below \(M_c\) in the "loose of critical" state. However, this might lead to some differences in the results when applied to simulations of samples initially on the "'loose of critical" side and using existing parameters as shown in below figure. However, compared to the reference simulations, the simulation results using the modified formulation of \(M_b\) respect the critical state.

---

1. Y. F. Dafalias and M. T. Manzari, ‘Simple plasticity sand model accounting for fabric change effects’, Journal of Engineering mechanics, vol. 130, no. 6, pp. 622–634, 2004. ↩