Triaxial Test - Consolidated Undrained Cyclic Loading using the HCA Model

Finite Element (FE) representation

The simulation of consolidated undrained cyclic triaxial test using the HCA model is an extension of the drained case explained here. Make sure to first look at this example before working on the undrained case because many aspects of the modelling are only explained in the drained example.

An axisymmetric two-phase element with eight solids nodes, quadratic shape functions for the displacement field and linear interpolation for the pore water pressure is used.

In a first initial step, the initial conditions are applied, i.e. initial stress (\(\sigma_1^0, \sigma_2^0\)), initial void ratio \(e_0\) or any other initial state variable required by the constitutive model

Two different cases are then simulated:

• Case 1): The strain amplitude \(\varepsilon^{ampl}\) is prescribed as initial condition without explicitly calculating it. In the second HCA step, the accumulation of deformations due to \(10^4\) cycles are simulated using the HCA model with a given strain amplitude of \(\varepsilon^{ampl}=3 \cdot 10^{-4}\).

• Case 2): The strain amplitude is calculated by simulating an individual cycle and recording the strain path. The hypoplastic model with intergranular strain extension is used to simulate two individual cycles (of which the second is used to calculate the strain amplitude). The HCA phase follows in the fourth step.

Constitutive model

The HCA model is used in combination with the hypoplastic model with intergranular strain extension for this example. The parameters for "Karlsruhe fine sand" for the HCA model are used and provided in the Table below.

\(C_{\textrm{ampl}}\)	\(C_{e}\)	\(C_{p}\)	\(C_{Y}\)	\(C_{N1}\)	\(C_{N2}\)	\(C_{N3}\)
1.33	0.60	0.23	1.68	2.95\(\cdot10^{-4}\)	0.41	\(1.9 \cdot 10^{-5}\)

Model generation

As single-element simulations do not involve complex geometries, we do not use a pre-processor and generate the input file by hand.

• First we create the eight nodes defining the finite element:

  *Node
  1, 0.0 , 0.00
  2, 0.05, 0.00
  3, 0.05, 0.1
  4, 0.00, 0.10
  5, 0.025, 0.00
  6, 0.05, 0.05
  7, 0.025, 0.1
  8, 0.00, 0.05
  

• We use an axisymmetric eight node element of type u8p4-sat-sat-ax (the element has 8 nodes with solid displacement degree of freedoms (dofs), 4 pore water pressure dofs, assumes a fully saturated state (-sat) and axisymmetric conditions).

*Element, Type = U8P4-sat-ax
1, 1, 2, 3, 4, 5, 6, 7, 8

• Next, we define some node and element sets for the assignment of boundary conditions, loads and material parameters:

  *Nset, Nset = nall
  1, 2, 3, 4, 5, 6, 7, 8 
  *Nset, Nset = nleft
  1, 4, 8
  *Nset, Nset = nright
  2 , 3, 6
  *Nset, Nset = nbottom
  1 , 2, 5
  *Nset, Nset = ntop
  3 , 4, 7
  *Elset, Elset = eall
  1
  

• In order to assign the material to the element, we first create a solid section. The material name linked to this solid section is arbitrary but must be specified in a later step.

  *Solid Section, elset = eall, material = soil
  

Sample numgeo input file using the strain amplitude from the experiment as input

In the first example, the strain amplitude is not calculated by a conventional constitutive model, but a measured amplitude from an experiment is used. This is typically the case if the simulations are performed to calibrate or check the parameters of the HCA model.

• Define the material: The material definition of the soil has to be changed in order to define a two-phase material (solid grains plus water) now. The bulk modulus of the pore water and the permeability have to be defined. In numgeo, the permeability equals the dynamic viscosity (set to \(10^{-6}\) kPas) multiplied with the hydraulic conductivity \(k^w\) and divided by the unit weight of water (\(\gamma_w = 10~\)kN/m\(^3\)). A hydraulic conductivity of \(k^w\) = 1 \(\cdot\) \(10^{-5}\) m/s is defined here. The resulting permeability of \(10^{-12}\) m\(^2\) is defined using *Permeability = isotropic. In addition to the material parameters, the HCA model requires the declaration of the step types. The first step is a low-cycle ("implicit") step. The actual HCA phase is performed in \(HCA\). The period of the cycles is 1 s.

*Material, name = soil, phases = 2

*Mechanical = HCA_Linear_Elasticity
5000.0,0.32
** Parameters of Karlsruhe fine sand
**CN1, CN2, CN3, Campl, Ce, 0, Cp2, 0
**Cy2, Cpi1, Cpi2, Cpi3, patm, eref, eps^ampl_ref, A
**a, n, nu, phic
0.000295,0.41,1.9e-05,1.33,0.6,0,0.23,0,
1.68,0,0,0,100.0,1.054,0.0001,1209,
1.63,0.5,0.32,0.578

*Bulk modulus
2.2d6

*Density
2.65, 1.0

*Permeability = isotropic
1e-12

*Dynamic viscosity
1d-6

*Implicit hca steps
Geostatic
*Explicit hca steps
HCA
*HCA cycle time
1

• Define the initial conditions of the simulation. In the present case this comprises the definition of the initial (effective) stresses, the initial void ratio and the strain amplitude. A value of \(\varepsilon^{ampl}=3\cdot 10^{-4}\) is set.

  *Initial conditions, type=stress, geostatic
  eall, 0.0, -150.0,  0.10, -150.0, 1.0, 1.0
  
  *Initial conditions, Type = state variables
  ** Initial relative density of 80 %
  eall, void_ratio, 0.818
  eall, strain_ampl, 3d-4
  *Initial conditions, Type = void ratio,default
  ** Initial relative density of 80 %
  eall,0.818
  

• As in most simulations in geotechnical engineering we start the simulation by initializing the geostatic stress field due to the self weight of the soil and any initial external loading without generating any deformations. In the present case, the initial stress field is solely given by the external load of 150 kPa acting isotropically on the sample. Since this is a very basic simulation, we do not request a field output but rely solely on the print output for evaluating the simulation results.

  *Step, name = Geostatic
  *Geostatic
  
  *Body force, instant
  eall, grav, 10.0, 0., -1, 0.
  *Dload, instant
  eall, p3, -150
  *Dload, instant
  eall, p2, -150
  *Boundary
  nleft, u1, 0.
  nbottom, u2, 0.
  *Boundary, Type=hydrostatic
  nall, pw, 0, 0.1
  *End Step
  

• In the second step \(10^4\) cycles are simulated using the HCA model. The initial increment is 0.2 s, the total step time is \(10^4\) s, the minimum allowed increment is 0.0001 s and the maximum increment is \(10^2\) s . Note that time does correspond to physical time in a transient step but corresponds in the present case to the number of cycles being simulated. During the analyses, the average total stresses are kept constant while excess pore water pressures can develop. The soil sample is free to settle and deform radially but because of the high bulk modulus of the water phase no volumetric strain occurs.

  *Step, name = HCA, inc = 10000000
  *Transient
  0.2, 10000, 0.0001,100
  
  *Body force, instant
  eall, grav, 10.0, 0., -1, 0.
  *Dload, instant
  eall, p3, -150
  *Dload, instant
  eall, p2, -150
  *Boundary
  nleft, u1, 0.
  nbottom, u2, 0.
  
  *output,print
  *node output, nset = ntop
  pw
  *Element output, Elset = eall
  S, E, void_ratio, strain_ampl, strain_acc, cyclic_history, fampl, fe, fp, fY
  *End Step
  

• We end the input file by using the "End Step" command.

  *End Input
  

Results

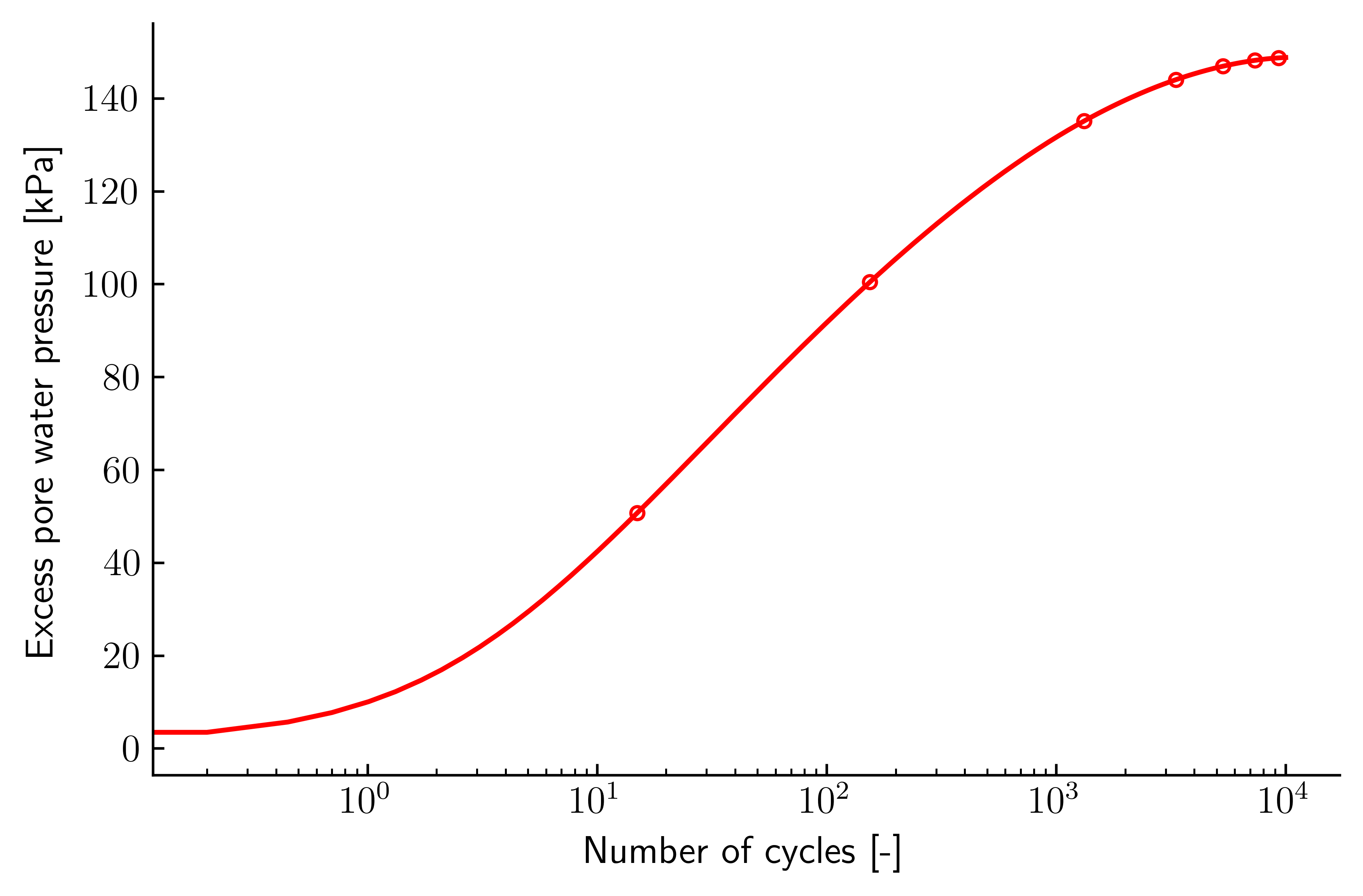
The accumulated excess pore water pressure vs. number of load cycles is given in Figure 1. Almost full liquefaction is reached after \(10^4\) cycles.

Python Script for plotting the results

The python script used to generate Figure 1 is given below:

import matplotlib
import matplotlib.pyplot as plt
import matplotlib.ticker as mtick
from pylab import genfromtxt
from matplotlib import rc
import os 
import numpy as np
dir_path = os.path.dirname(os.path.realpath(__file__))
plt.rcParams['backend'] = "pdf"
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
plt.rcParams['text.usetex'] = True
plt.rcParams['font.size'] = 12
plt.rcParams['axes.spines.right'] = False
plt.rcParams['axes.spines.top'] = False
plt.rcParams['axes.linewidth'] = 0.8 


#=============================================================================
# Read data
#%% =============================================================================


dirname = '/step-print-out'

dir_path = os.path.normpath(os.getcwd() +dirname)

sim1 = genfromtxt(dir_path+'/'+'NTOP_node_3.dat',skip_header=1)

#=============================================================================
# Plot first data
#%% =============================================================================
plt.figure(1)
plt.subplot(111)


plt.semilogx(sim1[:,0]-sim1[0,0],sim1[:,1],'or-',\
         markersize=4,markerfacecolor='none',markevery=20,\
         label=r'Simulation',clip_on=True)

ax = plt.gca()
ax.set_xlabel(r'Number of  cycles [-]')
ax.set_ylabel(r'Excess pore water pressure [kPa]',labelpad=7)


plt.tight_layout() 
fig = plt.gcf()  
fig.savefig('excess_pore_water_pressure_input_epsampl.pdf', dpi=600 , bbox_inches='tight')
fig.savefig('excess_pore_water_pressure_input_epsampl.png', dpi=600 , bbox_inches='tight')

Sample numgeo input file calculating the strain amplitude with a conventional model

In the second example, the strain amplitude is calculated by a conventional constitutive model, the hypoplastic model with intergranular strain extension in the present case. Having to calculate the strain amplitude is the case for a typical boundary value problem.

Only the modifications of the first example are explained in the following. The rest of the input file remains identical.

• The first two steps are low-cycle ("implicit") steps. The sinusoidal load is applied in FirstCycle and in SecCycle, whereby the strain curve is recorded for the latter. The actual HCA phase is performed in the step named HCA. The period of the cycles is 1 s.

  *Material, name = soil, phases = 2
  
  ** Parameters of Karlsruhe fine sand
  *mechanical = HCA_Hypoplasticity
  **phi, nu, hS, n, ed0, ec0, ei0, alpha
  **beta, mT, mR, R, betaR, chi, Kw
  0.577, 0.0, 4d6, 0.27, 0.677, 1.054, 1.15, 0.14
  2.5, 1.2, 2.4, 1d-4, 0.1, 6.0 , 0.
  *******
  **CN1, CN2, CN3, Campl, Ce, 0, Cp2, 0
  **Cy2, Cpi1, Cpi2, Cpi3, patm, eref, eps^ampl_ref, A
  **a, n, nu, phic
  0.000295, 0.41, 0.000019, 1.33, 0.6, 0, 0.23, 0
  1.68, 0, 0, 0, 100, 1.054, 0.0001, 1209
  1.63, 0.5, 0.32, 0.577
  
  *Bulk modulus
  2.2d6
  
  *Density
  2.65, 1.0
  
  *Permeability = isotropic
  1e-12
  
  *Dynamic viscosity
  1d-6
  
  *Implicit hca steps
  Geostatic, FirstCycle
  *Recording hca steps
  SecCycle
  *Explicit hca steps
  HCA
  *HCA cycle time
  1
  

• To apply cyclic loading, a sinusoidal amplitude with a frequency of 1 Hz is defined in addition.

  *Amplitude, name = sine1Hz, Type=periodic
  1, 0.0, 0.0, 6.283
  0.0, 1.0
  

• In the second and third step, one individual cycle is simulated in each step. The steps are defined identical.

  ** ----------------------------------------
  
  *Step, name = FirstCycle, inc = 10000000
  *Transient
  0.01, 1, 0.0001, 0.05
  
  *Body force, instant
  eall, grav, 10.0, 0., -1, 0.
  *Dload, instant
  eall, p3, -150
  *Dload, instant
  eall, p2, -150
  
  *Dload, amplitude=sine1Hz
  eall, P3, -60
  
  *Boundary
  nleft, u1, 0.
  nbottom, u2, 0.
  
  *output,print
  *node output, nset = ntop
  pw
  *Element output, Elset = eall
  S, E, void_ratio
  *End Step
  
  ** ----------------------------------------
  
  *Step, name = SecCycle, inc = 10000000
  *Transient
  0.01, 1, 0.0001, 0.05
  
  *Body force, instant
  eall, grav, 10.0, 0., -1, 0.
  *Dload, instant
  eall, p3, -150
  *Dload, instant
  eall, p2, -150
  
  *Dload, amplitude=sine1Hz
  eall, P3, -60
  
  *Boundary
  nleft, u1, 0.
  nbottom, u2, 0.
  
  *output,print
  *node output, nset = ntop
  pw
  *Element output, Elset = eall
  S, E, void_ratio
  *End Step
  

The HCA step remains unchanged.

Results

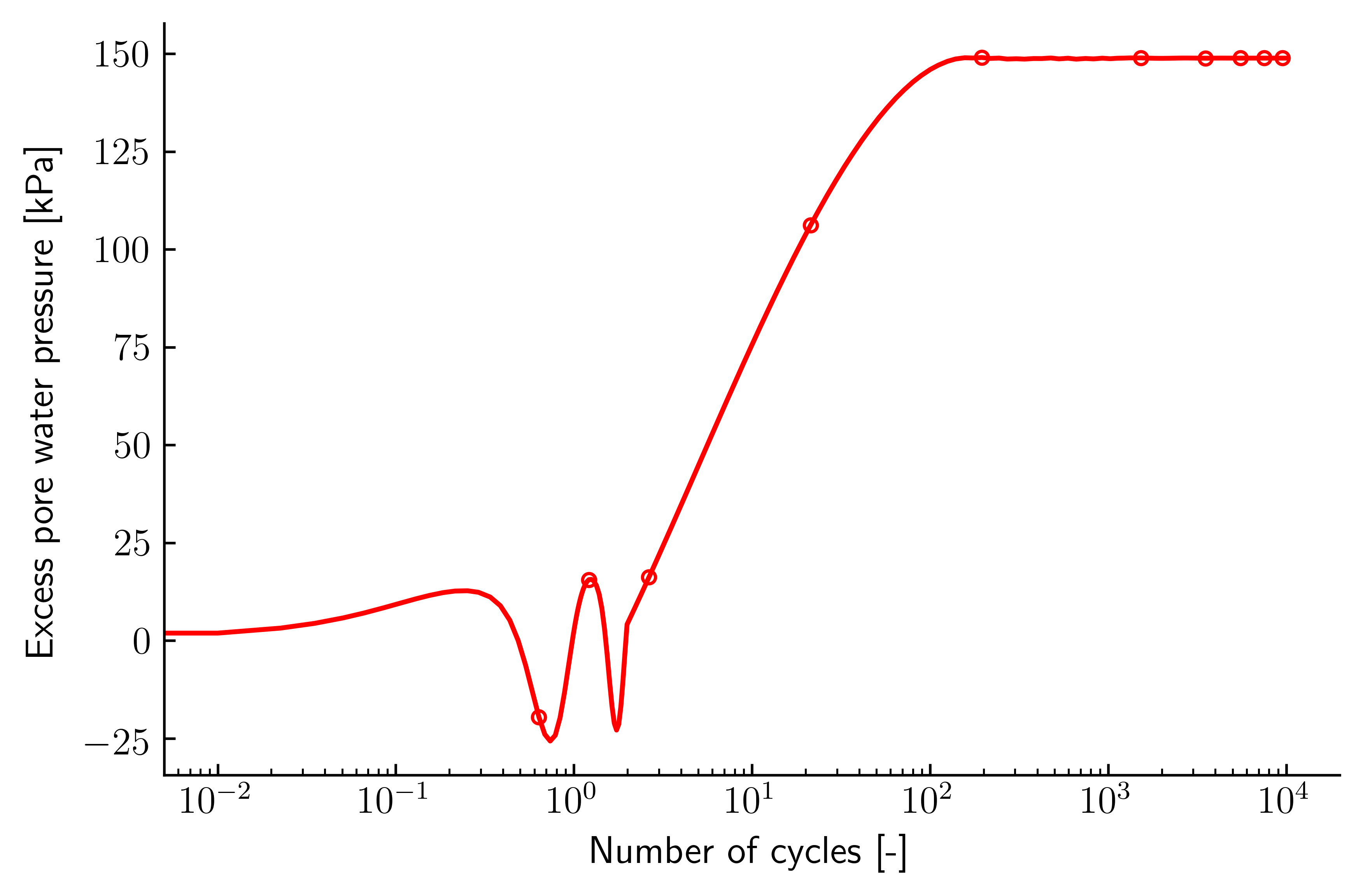
The accumulated permanent axial strain versus number of load cycles is given in Figure 2. The simulated individual cycle is well visible and liquefaction is reached very early.

Complete input file for a predefined strain amplitude

The complete input file is given below.

**=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=
**                                  numgeo                                    
**             Copyright (C) 2024 Jan Machacek, Patrick Staubach              
**=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=

**=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=
**
**
** For this simple problem we do not need to define any parts or sections
**
**
*Node
1, 0.0 , 0.00
2, 0.05, 0.00
3, 0.05, 0.1
4, 0.00, 0.10
5, 0.025, 0.00
6, 0.05, 0.05
7, 0.025, 0.1
8, 0.00, 0.05

** ----------------------------------------

*Nset, Nset = nall
1, 2, 3, 4, 5, 6, 7, 8 
*Nset, Nset = nleft
1, 4, 8
*Nset, Nset = nright
2 , 3, 6
*Nset, Nset = nbottom
1 , 2, 5
*Nset, Nset = ntop
3 , 4, 7

** ----------------------------------------

*Element, Type = U8P4-sat-ax
1, 1, 2, 3, 4, 5, 6, 7, 8

** ----------------------------------------

*Elset, Elset = eall
1

** ----------------------------------------

*Solid Section, Elset = eall, material=soil

** ----------------------------------------

*Material, name = soil, phases = 2

*Mechanical = HCA_Linear_Elasticity
5000.0,0.32
** Parameters of Karlsruhe fine sand
0.000295,0.41,1.9e-05,1.33,0.6,0,0.23,0,
1.68,0,0,0,100.0,1.054,0.0001,1209,
1.63,0.5,0.32,0.578

*Bulk modulus
2.2d6

*Density
2.65, 1.0

*Permeability = isotropic
1e-12

*Dynamic viscosity
1d-6

*Implicit hca steps
Geostatic
*Explicit hca steps
HCA
*HCA cycle time
1

** ----------------------------------------

*Initial conditions, type=stress, geostatic
eall, 0.0, -150.0,  0.10, -150.0, 1.0, 1.0

*Initial conditions, Type = state variables
** Initial relative density of 80 %
eall, void_ratio, 0.818
eall, strain_ampl, 3d-4
*Initial conditions, Type = void ratio,default
** Initial relative density of 80 %
eall,0.818

** ----------------------------------------

*Step, name = Geostatic
*Geostatic

*Body force, instant
eall, grav, 10.0, 0., -1, 0.
*Dload, instant
eall, p3, -150
*Dload, instant
eall, p2, -150
*Boundary
nleft, u1, 0.
nbottom, u2, 0.
*Boundary, Type=hydrostatic
nall, pw, 0, 0.1
*End Step

** ----------------------------------------

*Step, name = HCA, inc = 10000000
*Transient
0.2, 10000, 0.0001,100

*Body force, instant
eall, grav, 10.0, 0., -1, 0.
*Dload, instant
eall, p3, -150
*Dload, instant
eall, p2, -150
*Boundary
nleft, u1, 0.
nbottom, u2, 0.

*output,print
*node output, nset = ntop
pw
*Element output, Elset = eall
S, E, void_ratio, strain_ampl, strain_acc, cyclic_history, fampl, fe, fp, fY
*End Step

** ----------------------------------------

*End Input

Complete input file calculating the strain amplitude

The complete input file is given below.

**=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=
**                                  numgeo                                    
**             Copyright (C) 2024 Jan Machacek, Patrick Staubach              
**=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=

**=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=~~=
**
**
** For this simple problem we do not need to define any parts or sections
**
**
*Node
1, 0.0 , 0.00
2, 0.05, 0.00
3, 0.05, 0.1
4, 0.00, 0.10
5, 0.025,0.00
6, 0.05,0.05
7, 0.025,0.1
8, 0.00,0.05

** ----------------------------------------

*Nset, Nset = nall
1, 2, 3, 4, 5, 6, 7, 8 
*Nset, Nset = nleft
1, 4, 8
*Nset, Nset = nright
2 , 3, 6
*Nset, Nset = nbottom
1 , 2, 5
*Nset, Nset = ntop
3 , 4, 7

** ----------------------------------------

*Element, Type = U8P4-sat-ax
1, 1, 2, 3, 4, 5, 6, 7, 8

** ----------------------------------------

*Elset, Elset = eall
1

** ----------------------------------------

*Solid Section, Elset = eall, material=soil

** ----------------------------------------

*Material, name = soil, phases = 2

** Parameters of Karlsruhe fine sand
*mechanical = HCA_Hypoplasticity
**phi, nu, hS, n, ed0, ec0, ei0, alpha
**beta, mT, mR, R, betaR, chi, Kw
0.577, 0.0, 4d6, 0.27, 0.677, 1.054, 1.15, 0.14
2.5, 1.2, 2.4, 1d-4, 0.1, 6.0 , 0.
*******
**CN1, CN2, CN3, Campl, Ce, 0, Cp2, 0
**Cy2, Cpi1, Cpi2, Cpi3, patm, eref, eps^ampl_ref, A
**a, n, nu, phic
0.000295, 0.41, 0.000019, 1.33, 0.6, 0, 0.23, 0
1.68, 0, 0, 0, 100, 1.054, 0.0001, 1209
1.63, 0.5, 0.32, 0.577

*Bulk modulus
2.2d6

*Density
2.65, 1.0

*Permeability = isotropic
1e-12

*Dynamic viscosity
1d-6

*Implicit hca steps
Geostatic, FirstCycle
*Recording hca steps
SecCycle
*Explicit hca steps
HCA
*HCA cycle time
1
** ----------------------------------------

*Initial conditions, type=stress, geostatic
eall, 0.0, -150.0,  0.10, -150.0, 1.0, 1.0

*Initial conditions, Type = state variables
** Initial relative density of 80 %
eall, void_ratio, 0.818

*Initial conditions, Type = void ratio,default
** Initial relative density of 80 %
eall,0.818

** ----------------------------------------

*Amplitude, name = sine1Hz, Type=periodic
1, 0.0, 0.0, 6.283
0.0, 1.0

** ----------------------------------------

*Step, name = Geostatic
*Geostatic

*Body force, instant
eall, grav, 10.0, 0., -1, 0.
*Dload, instant
eall, p3, -150
*Dload, instant
eall, p2, -150
*Boundary
nleft, u1, 0.
nbottom, u2, 0.
*Boundary, Type=hydrostatic
nall, pw, 0, 0.1
*End Step

** ----------------------------------------

*Step, name = FirstCycle, inc = 10000000
*Transient
0.01, 1, 0.0001, 0.05

*Body force, instant
eall, grav, 10.0, 0., -1, 0.
*Dload, instant
eall, p3, -150
*Dload, instant
eall, p2, -150

*Dload, amplitude=sine1Hz
eall, P3, -60

*Boundary
nleft, u1, 0.
nbottom, u2, 0.

*output,print
*node output, nset = ntop
pw
*Element output, Elset = eall
S, E, void_ratio
*End Step

** ----------------------------------------

*Step, name = SecCycle, inc = 10000000
*Transient
0.01, 1, 0.0001, 0.05

*Body force, instant
eall, grav, 10.0, 0., -1, 0.
*Dload, instant
eall, p3, -150
*Dload, instant
eall, p2, -150

*Dload, amplitude=sine1Hz
eall, P3, -60

*Boundary
nleft, u1, 0.
nbottom, u2, 0.

*output,print
*node output, nset = ntop
pw
*Element output, Elset = eall
S, E, void_ratio
*End Step
** ----------------------------------------


*Step, name = HCA, inc = 10000000
*Transient
0.2, 10000, 0.0001,100

*Body force, instant
eall, grav, 10.0, 0., -1, 0.
*Dload, instant
eall, p3, -150
*Dload, instant
eall, p2, -150
*Boundary
nleft, u1, 0.
nbottom, u2, 0.

*output,print
*node output, nset = ntop
pw
*Element output, Elset = eall
S, E, void_ratio, strain_ampl, strain_acc, cyclic_history, fampl, fe, fp, fY
*End Step

** ----------------------------------------

*End Input