Three-phase porous solid elements (u-p-p elements)

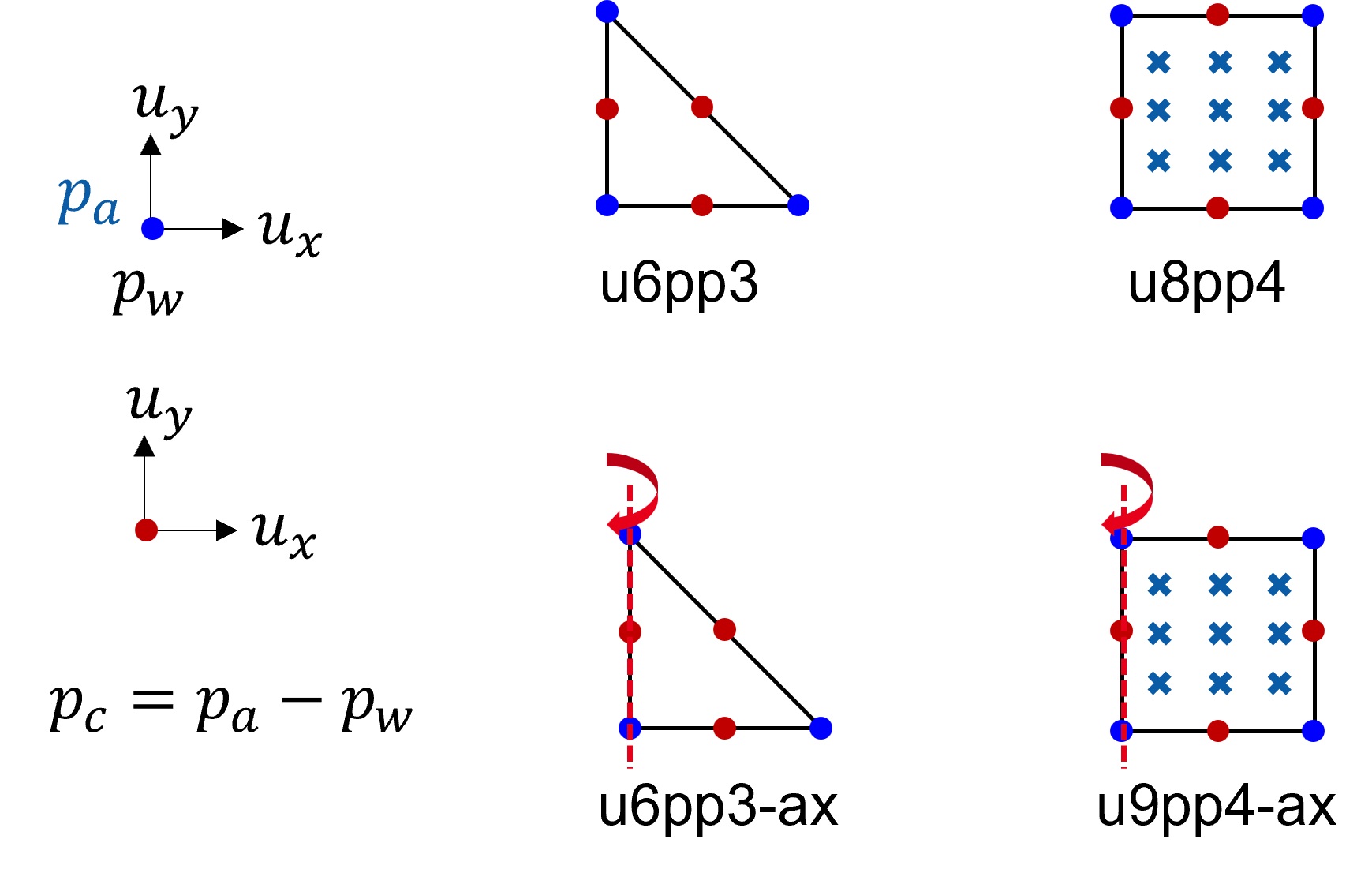
These elements are implemented for simulating the response of a three-phase solid-fluid fully coupled material, based on Theory of Porous Media. The porous medium is assumed to be composed of one solid phase (e.g. the grain skeleton) and two pore-fluids (e.g. water and air). The following elements correspond to the "full" formulation, where both pore-fluids can be controlled

In the "full" formulation of the three-phase elements both pore-fluids are discretized at the nodes of the element. Thus, each node has 4 degrees of freedom, the solid displacements \(u_1\) and \(u_2\) as well as the pore-fluid pressures \(p^w\) and \(p^w\). The capillary pressure is calculated using \(p^c=p^a-p^w\). The following elements are available:

2D Elements

Element label	Dim.	Shape	Nodes	Interpolation Order	nIP*	Remarks
u6pp3	2D	triangle	6	quadratic	3	(1), (2)
u8pp4	2D	rectangle	8	quadratic	9	(1), (2)

Axisymmetric Elements

Element label	Dim.	Shape	Nodes	Interpolation Order	nIP*	Remarks
u6pp3-ax	axisym.	triangle	6	quadratic	3	(1), (2)
u8pp4-ax	axisym.	rectangle	8	quadratic	9	(1), (2)

Remarks

*	nIP = number of integration points
(1)	Due to the full integration, the element will behave badly for isochoric material behavior. This shortcoming is more pronounced for linear interpolated elements and less pronounced for quadratic interpolated ones.
(2)	Taylor-Hood formulation: The solid displacements \(u\) are interpolated using quadratic shape functions, whereas the pore-fluid pressures \(p^w\) and \(p^a\) are interpolated using linear shape functions.

Notice that these elements require the definition of a three-phase material: (*Material,..., Phases=3) as described in *Material. In addition, a saturation-suction relation and relative permeability models have to be prescribed.