Skip to content

Monopile under high-cyclic loading

Finite Element (FE) representation

Tip

The mesh file for quadratically interpolated elements are found here. The full input files here.

Warning

If you are not able to use user-subroutines (because you have not installed OneAPI), a reduced version of the input files without the need for user-subroutines is found here. Note that in this input file a mesh with linearly interpolated elements is used in order to speed up the simulation.

This example explains the simulation of the long-term response of monopile foundations using the HCA model in combination with the hypoplastic model with intergranular strain. The mesh generation is skipped for this example.

The adopted finite element model is given in Figure 1. The pile has a length of 10 m and a diameter of 4 m. The file containing the mesh (mesh.inp) is discussed first and then the step file (step_tutorial.inp) is addressed.

figure 1 Figure 1. Model of the monopile (only the corner nodes of the elements are visible)

Running out of RAM

The simulation needs quite a bit of RAM. If your simulation is killed, the RAM of your computer is not enough.

Mesh

For the soil, three-dimensional u-p finite elements with 27 nodes discretising the displacement u of the solid phase and 8 nodes discretising the pore water pressure \(p^w\) are utilised (termed u27p8 element, obtained using the bi-quadratic option in the element definition since the pre-processor generated u20 elements).

.
.
*Element, type=u20p8-sat,bi-quadratic
.
.

Hence, quadratic interpolation functions are used for the solid displacement while linear interpolation functions are applied for the pore water pressure (i.e. Taylor-Hood element formulation 1). The u27p8 element is superior to the u20p8 element in contact analyses.

The pile is modelled with single phase elements with 27 nodes (u27-solid obtained again using the bi-quadratic option).

.
.
*Element, type=u20-solid,bi-quadratic
.
.

Properties, Initial conditions and step definitions

Properties, contact and Initial conditions

The step file (step_tutorial.inp) first includes the mesh file by defining:

*include=mesh

Then the material definitions are given. The pile is composed of two materials: the regular steel material and a much stiffer material used only for the uppermost row of elements where the load is applied to the pile. This is done to avoid excessive deformations of the pile at the point of load application.

*Material, name=Elastisch_Stahl, phases = 1
*Density
30.9416d0
*Mechanical = Linear_Elasticity
2.1e+8, 0.3
**
*Material, name=Stahl_kopf, phases = 1
*Density
30.9416d0
*Mechanical = Linear_Elasticity
2.1e+12, 0.3

Note that the density is set higher in order to consider an additional length of the pile not modelled.

For the low-cycle phase of the HCA model, the Hypoplastic model with intergranular strain extension is used. The parameters calibrated for "Karlsruhe fine sand" are adopted. The parameters for the HCA model are provided in the Table below

\(C_{\textrm{ampl}}\) \(C_{e}\) \(C_{p}\) \(C_{Y}\) \(C_{N1}\) \(C_{N2}\) \(C_{N3}\)
1.33 0.60 0.23 1.68 2.95\(\cdot10^{-4}\) 0.41 \(1.9 \cdot 10^{-5}\)

Two densities have to be given which are the density of the solid grains and the density of water. In addition, the bulk modulus of the pore water and the permeability have to be defined. In numgeo, the permeability equals the dynamic viscosity (set to \(10^{-6}\) kPas) multiplied with the hydraulic conductivity \(k^w\) and divided by the unit weight of water (\(\gamma_w = 10~\)kN/m\(^3\)). A high hydraulic conductivity of \(k^w\) = 1 \(\cdot\) \(10^{-3}\) m/s is defined here. The resulting permeability of \(10^{-10}\) m\(^2\) is set in the input file.

To avoid positive mean effective stresses (in mechanical sign convention), a minimum value is set. In addition, an artificial viscosity is used to achieve better convergence. However, it is not necessarily required and also doesn't influence the results.

In addition to the material parameters, the HCA model requires the declaration of the step types. The first four steps are low-cycle ("implicit") steps. The first sinusoidal load is applied in \(step4\). In \(step5\) the second cycle is applied, for which the strain path is recorded. The actual HCA phase is performed in \(step6\). The period of the cycles is 1 s for why in line 40 to 41 the cycle time is set to 1 s.

*Material, name = hypo, phases = 2
*Mechanical = HCA_Hypoplasticity
**phi, nu, hS, n, ed0, ec0, ei0, alpha
**beta, mT, mR, R, betaR, chi, Kw
0.577, 0.0, 4d6, 0.27, 0.677, 1.054, 1.15, 0.14
2.5, 1.2, 2.4, 1d-4, 0.1, 6.0 , 0.
*******
**CN1, CN2, CN3, Campl, Ce, 0, Cp2, 0
**Cy2, Cpi1, Cpi2, Cpi3, patm, eref, eps^ampl_ref, A
**a, n, nu, phic
0.000295, 0.41, 0.000019, 1.33, 0.6, 0, 0.23, 0
1.68, 0, 0, 0, 100, 1.054, 0.0001, 1209
1.63, 0.5, 0.32, 0.577

*Density
2.7d0, 1.0


*minpressure
-0.05

*mechanical viscosity = linear
0.5,2.0,1.1,1.5,1.1,1.5

*Bulk modulus
2.2d5

*Permeability=ISOTROPIC
1.0e-10
** k = 1.0e-10 * 1.0e-6 * 10 = 1.0e-3
*Dynamic viscosity
1.0e-6

*Implicit hca steps
step1,step2,step3,step4
*Recording hca steps
step5
*Explicit hca steps
step6
*HCA cycle time
1

The penalty method is used to enforce the contact constraints. No separation between soil and pile is possible once the contact is active. A simple Coulomb friction model with a friction coefficient of 0.3 is used.

The contact between soil and pile is discretised using a mortar contact discretisation technique.

A small value for the contact clearance is defined, which leads to a small value of initial contact pressure. This is beneficial since the Initial stress state is closer to equilibrium, in which the earth pressure is acting as contact pressure.

*Interaction,name=pen,MECHANICAL=penalty,no separation
*friction, model=MC,stiffness_factor=0.02
0.3,0,0

*Contact Pair,interaction=pen,discretisation=element mortar
BodenMonopileAussenSurface,MonopileAussenSurface
BodenMonopileInnenSurface,MonopileInnenSurface
BodenPfahlfussSurface,MonopileUntenSurface
*contact options, name=pen, clearance=1d-6

The Initial conditions for stress and state variables are defined in user subroutines (see the files shipped with this document). The void ratio used for the calculation of the density is given in addition. This value does not necessary have to coincide with the value given in the user Initial state file. A hydrostatic pore water pressure is defined for the entire soil mass.

**---------------------------------- Initial conditions -----------------------------
** 
*Initial conditions, type=stress, user

*Initial conditions, type=state variables, user
Geometrie_Bodenkoerper_Aussen4
Geometrie_Bodenkoerper_Aussen5
Geometrie_Bodenkoerper_Innen4

*Initial conditions, type=void ratio, default
BodenInstance.BodenAlle,0.7524d0

*Initial conditions, type=pore water pressure, default
BodenInstance.BodenAlle, 0.0d0, 0.0d0, 50.0d0, 500.0d0

For the analysis, different time distributions of boundary and loading conditions have to be defined. This is done using the following Amplitude definitions:

*Amplitude, Name = LoadingRamp , Type = RAMP
0.0, 0.0, 1.0d0, 1.0d0
*Amplitude, Name = Sinus1Hz , Type = PERIODIC
1,0.0,0.0,6.28
0,1

The Amplitude \(LoadingRamp\) defines a linear increase of a quantity beginning with the relative value 0 at the time \(t_1=0\) and the relative value 1 at the time \(t_2=1\). To apply the cyclic loading, a sinusoidal Amplitude with a frequency of 1 Hz is defined in addition.

Steps and loading definitions

The first step is defined below. The analysis type of the step is a static step. The keyword Body force imposes a gravitational force which is applied instantaneous (Instant). The element sets \(BodenInstance.BodenAlle\) and \(MonopileInstance.MonopileAlle\) are loaded by the gravity (Amplitude \(10\) m/s\(^2\), directed downwards with the normalized vector of the gravity \(\vec{\textbf{b}}=\{0,0,1\}\)).

All nodes of the pile and the soil are constraint in 1-, 2- and 3-direction. Therefore, no displacement is possible for any Node in the model. The pore water pressure is prescribed hydrostatically using a user subroutine (see the files shipped with this document). The error controls are modified and only the local convergence controls are set active.

The output is written in the vtk format (suitable for ParaView) and is of ASCII type. The Node output includes the displacement (U) and pore water pressure (PW) of the nodes. The element output includes the stress (S) as well as the void ratio (Void_ratio) and the contact output variables (Contact). The contact output contains contact stresses as well as contact distances for each contact Node. In addition, a print output is defined. The displacement and the pore water pressure is printed for several nodes of the model.

** STEP: Eigengewicht_Boden
** 

*Step, name=step1,inc=1
*static
1,1,1d-4,1

** LOADS


*Body force, Instant
BodenInstance.BodenAlle, GRAV, 10., 0., 0., 1.

*Body force, Instant
MonopileInstance.MonopileAlle, GRAV, 10., 0., 0., 1.

*Boundary
MonopileInstance.MonopileAlle, u1,0.0d0
MonopileInstance.MonopileAlle, u2,0.0d0
MonopileInstance.MonopileAlle, u3,0.0d0
BodenInstance.BodenAlle, u1,0.0d0
BodenInstance.BodenAlle, u2,0.0d0
BodenInstance.BodenAlle, u3,0.0d0
*Uboundary
BodenInstance.BodenAlle, pw,1.0d0

*Controls, global, deactivate
*Controls, u, activate

*output, field, vtk, ASCII
*Node output, nset = BodenInstance.BodenAlle
U,pw
*element output, elset = BodenInstance.BodenAlle
S, Contact, void_ratio
*output, print
*Node output, nset = Knoten_Monopile_Aussen_Oben_Links
U
*Node output, nset = Knoten_Monopile_Aussen_Oben_Links
U
*Node output, nset = Monopile_Symmetrie_Vorne
U, coords
*Node output, nset = PWD_rechts_oben
U, coords, pw
*Node output, nset = PWD_links_oben
U, coords, pw
*Node output, nset = PWD_rechts_unten
U, coords, pw
*Node output, nset = PWD_links_unten
U, coords, pw
*End STEP

In the second step the correct boundary conditions of the model are established. The back-side of the soil is constraint in the two horizontal directions. The bottom is constraint in the vertical direction. The symmetry axis of both parts of the model is constraint in the y-direction (see Figure 1)

A vertical loading is applied to the monopile head. The left and the right top node of the pile are gradually loaded by 500 kN over the course of the step. An additional surface pressure on the top of the model is applied. The output remains identical to the first step.

** 
*Step, name=step2,inc=100
*static
0.5,1,1d-4,1

** LOADS

*Body force, Instant
BodenInstance.BodenAlle, GRAV, 10., 0., 0., 1.

*Body force, Instant
MonopileInstance.MonopileAlle, GRAV, 10., 0., 0., 1.

** BOUNDARY CONDITIONS
*Boundary
Boden_Hinten,u1,0.0d0
Boden_Hinten,u2,0.0d0
Boden_Unten_S5,u3,0.0d0
Boden_Symmetrie_Vorne_Links, u2,0.0d0
Boden_Symmetrie_Vorne_Mitte, u2,0.0d0
Monopile_Symmetrie_Vorne,u2,0.0d0
Boden_Symmetrie_Vorne_Rechts, u2,0.0d0
*Uboundary
BodenInstance.BodenAlle, pw,1.0d0

** LOADS


*Cload,Amplitude=LoadingRamp
Knoten_Monopile_Aussen_Oben_Rechts, 3, 500
*Cload,Amplitude=LoadingRamp
Knoten_Monopile_Aussen_Oben_Links, 3, 500

*Dload,Instant
_BodenObenS1Surface_S2,P2,-3d0
*Dload ,Instant
_BodenObenS1Surface_S3,P3,-3d0


*Controls, global, deactivate
*Controls, u, modify
0.05,0.05,0.08,1e-7,1e-7, 3

*output, field, vtk, ASCII
*Node output, nset = BodenInstance.BodenAlle
U,pw
*element output, elset = BodenInstance.BodenAlle
S, Contact, void_ratio
*output, print
*Node output, nset = Knoten_Monopile_Aussen_Oben_Links
U
*Node output, nset = Knoten_Monopile_Aussen_Oben_Links
U
*Node output, nset = Monopile_Symmetrie_Vorne
U, coords
*Node output, nset = PWD_rechts_oben
U, coords, pw
*Node output, nset = PWD_links_oben
U, coords, pw
*Node output, nset = PWD_rechts_unten
U, coords, pw
*Node output, nset = PWD_links_unten
U, coords, pw
*End STEP

In the third step the mean value of horizontal loading is applied. The left and the right top node of the pile are gradually loaded by 50 kN in horizontal direction and a moment (represented by a vertical force pair) of \(600\cdot2\cdot2 = 2400\) kNm over the course of the step. The other definitions remain identical to the previous step.

** 
*Step, name=step3,inc=100
*static
0.05,1.0d0,1d-4,0.05
** 
** LOADS

*Body force, Instant
BodenInstance.BodenAlle, GRAV, 10., 0., 0., 1.

*Body force, Instant
MonopileInstance.MonopileAlle, GRAV, 10., 0., 0., 1.

** BOUNDARY CONDITIONS
*Boundary
Boden_Hinten,u1,0.0d0
Boden_Hinten,u2,0.0d0
Boden_Unten_S5,u3,0.0d0
Boden_Symmetrie_Vorne_Links, u2,0.0d0
Boden_Symmetrie_Vorne_Mitte, u2,0.0d0
Monopile_Symmetrie_Vorne,u2,0.0d0
Boden_Symmetrie_Vorne_Rechts, u2,0.0d0

*Uboundary
BodenInstance.BodenAlle, pw,1.0d0

** 
** LOADS
** 
*cload,Instant
Knoten_Monopile_Aussen_Oben_Rechts, 3, 500
*cload,Instant
Knoten_Monopile_Aussen_Oben_Links, 3, 500

*Cload,Amplitude=LoadingRamp
Knoten_Monopile_Aussen_Oben_Rechts, 1, -50

*Cload,Amplitude=LoadingRamp
Knoten_Monopile_Aussen_Oben_Links, 1, -50

*Cload,Amplitude=LoadingRamp
Knoten_Monopile_Aussen_Oben_Rechts, 3, 600

*Cload,Amplitude=LoadingRamp
Knoten_Monopile_Aussen_Oben_Links, 3, -600

*Dload,Instant
_BodenObenS1Surface_S2,P2,-3d0
*Dload ,Instant
_BodenObenS1Surface_S3,P3,-3d0
**
*Controls, global, deactivate
*Controls, u, modify
0.04,0.04,0.04,1e-7,1e-7,3
*Controls, pw, deactivate
**
*output, field, vtk, ASCII
*Node output, nset = BodenInstance.BodenAlle
U,pw,V,A
*element output, elset = BodenInstance.BodenAlle
S, Contact, void_ratio,contact_diagnostic
*output, print
*Node output, nset = Knoten_Monopile_Aussen_Oben_Links
U
*Node output, nset = Monopile_Symmetrie_Vorne
U, coords
*Node output, nset = PWD_rechts_oben
U, coords, pw
*Node output, nset = PWD_links_oben
U, coords, pw
*Node output, nset = PWD_rechts_unten
U, coords, pw
*Node output, nset = PWD_links_unten
U, coords, pw
*End STEP

The fourth and fifth step are identical (expect of the step name). The horizontal sinusoidal load is applied, which also has a component in horizontal direction and a moment component. Note that for this example no effects from excess pore water pressure and consolidation are accounted for because the simulation is faster. This is defined by setting the step to static and constraining the pore water pressure in the entire model. If one would want to consider these effects, the type of analysis has to be changed to a transient calculation, including pore water pressure change and water flow (consolidation). In addition, the boundary condition for the pore water pressure would have to be deleted. The boundary conditions for Boden_Oben_S1 and Boden_hinten would in this case allow for drainage at the top and the back of the model. In the current definition as static step they are obsolete.

** 
*Step, name=step4,inc=1000, no cut back
*static
0.05,1.0d0,1d-4,0.05
** 
** LOADS

*Body force, Instant
BodenInstance.BodenAlle, GRAV, 10., 0., 0., 1.

*Body force, Instant
MonopileInstance.MonopileAlle, GRAV, 10., 0., 0., 1.

** BOUNDARY CONDITIONS
*Boundary
Boden_Hinten,u1,0.0d0
Boden_Hinten,u2,0.0d0
Boden_Unten_S5,u3,0.0d0
Boden_Symmetrie_Vorne_Links, u2,0.0d0
Boden_Symmetrie_Vorne_Mitte, u2,0.0d0
Monopile_Symmetrie_Vorne,u2,0.0d0
Boden_Symmetrie_Vorne_Rechts, u2,0.0d0
*boundary
Boden_Oben_S1, pw,0.0d0
*uboundary
Boden_hinten, pw,1.0d0
Boden_Unten_S5, pw,1.0d0
** 
** LOADS
** 
*cload,Instant
Knoten_Monopile_Aussen_Oben_Rechts, 3, 500
*cload,Instant
Knoten_Monopile_Aussen_Oben_Links, 3, 500
*Cload,Instant
Knoten_Monopile_Aussen_Oben_Rechts, 1, -50

*Cload,Instant
Knoten_Monopile_Aussen_Oben_Links, 1, -50

*Cload,Instant
Knoten_Monopile_Aussen_Oben_Rechts, 3, 600

*Cload,Instant
Knoten_Monopile_Aussen_Oben_Links, 3, -600

*Cload, Amplitude=Sinus1Hz
Knoten_Monopile_Aussen_Oben_Rechts, 3, 600

*Cload, Amplitude=Sinus1Hz
Knoten_Monopile_Aussen_Oben_Links, 3, -600

*Cload, Amplitude=Sinus1Hz
Knoten_Monopile_Aussen_Oben_Rechts, 1, -50

*Cload, Amplitude=Sinus1Hz
Knoten_Monopile_Aussen_Oben_Links, 1, -50
*Dload,Instant
_BodenObenS1Surface_S2,P2,-3d0
*Dload ,Instant
_BodenObenS1Surface_S3,P3,-3d0
*Uboundary
BodenInstance.BodenAlle, pw,1.0d0

** 
**
*Controls, global, deactivate
*Controls, u, modify
0.04,0.04,0.04,1e-7,1e-7,3
*Controls, pw, deactivate
**
*output, field, vtk, ASCII
*frequency=5
*Node output, nset = BodenInstance.BodenAlle
U,pw,V,A
*element output, elset = BodenInstance.BodenAlle
S, Contact, void_ratio
*output, print
*Node output, nset = Knoten_Monopile_Aussen_Oben_Links
U
*Node output, nset = Monopile_Symmetrie_Vorne
U, coords
*Node output, nset = PWD_rechts_oben
U, coords, pw
*Node output, nset = PWD_links_oben
U, coords, pw
*Node output, nset = PWD_rechts_unten
U, coords, pw
*Node output, nset = PWD_links_unten
U, coords, pw
*End STEP

Lastly, the HCA step is defined in step 6 simulating \(10^6\) further cycles. Only the mean value of load is applied in this step. The strain Amplitude was automatically calculated at the end of step 5. Some HCA-specific output variables are requested.

** 
*Step, name=step6,inc=100000
*static
1,1d6,1d-4,1d4
** 
** LOADS

*Body force, Instant
BodenInstance.BodenAlle, GRAV, 10., 0., 0., 1.

*Body force, Instant
MonopileInstance.MonopileAlle, GRAV, 10., 0., 0., 1.

** BOUNDARY CONDITIONS
*Boundary
Boden_Hinten,u1,0.0d0
Boden_Hinten,u2,0.0d0
Boden_Unten_S5,u3,0.0d0
Boden_Symmetrie_Vorne_Links, u2,0.0d0
Boden_Symmetrie_Vorne_Mitte, u2,0.0d0
Monopile_Symmetrie_Vorne,u2,0.0d0
Boden_Symmetrie_Vorne_Rechts, u2,0.0d0
*boundary
Boden_Oben_S1, pw,0.0d0
*uboundary
Boden_hinten, pw,1.0d0
Boden_Unten_S5, pw,1.0d0
** 
** LOADS
** 
*cload,Instant
Knoten_Monopile_Aussen_Oben_Rechts, 3, 500
*cload,Instant
Knoten_Monopile_Aussen_Oben_Links, 3, 500

*Cload,Instant
Knoten_Monopile_Aussen_Oben_Rechts, 1, -50

*Cload,Instant
Knoten_Monopile_Aussen_Oben_Links, 1, -50

*Cload,Instant
Knoten_Monopile_Aussen_Oben_Rechts, 3, 600

*Cload,Instant
Knoten_Monopile_Aussen_Oben_Links, 3, -600
*Dload,Instant
_BodenObenS1Surface_S2,P2,-3d0
*Dload ,Instant
_BodenObenS1Surface_S3,P3,-3d0
*Uboundary
BodenInstance.BodenAlle, pw,1.0d0
** 

**
*Controls, global, deactivate
*Controls, u, modify
0.12,0.12,0.08,1e-7,1e-7,3
**
*output, field, vtk, ASCII
*frequency=5
*Node output, nset = BodenInstance.BodenAlle
U,pw
*element output, elset = BodenInstance.BodenAlle
S, Contact, void_ratio, Strain_ampl, Strain_acc, cyclic_history, fe, fampl, fy, fp, 
*output, print
*Node output, nset = Knoten_Monopile_Aussen_Oben_Links
U
*Node output, nset = Monopile_Symmetrie_Vorne
U, coords
*Node output, nset = PWD_rechts_oben
U, coords, pw
*Node output, nset = PWD_links_oben
U, coords, pw
*Node output, nset = PWD_rechts_unten
U, coords, pw
*Node output, nset = PWD_links_unten
U, coords, pw
*End STEP

The calculation is started by calling numgeo over the command line, specifying the name of the input file step (without ending), confirming by pressing enter, specifying the number of CPUs (depending on the hardware, 4 CPUs are appropriated here) and pressing enter again.

Results of the simulation

After the calculation is finished (the command window is ready for a new command), open the .sta file first and check that the simulation was successful by identifying that both steps have been completed successfully. If the calculation immediately stops, check the error message in the .log file and if any error files were generated in the calculation folder.

To see the output of the calculation, start ParaView and open the pvd file (in the right upper options bar: "File" \(\rightarrow\) "Open...").

The field of the strain amplitude and the final deformed configuration after \(10^6\) cycles (5-times enhanced) is given in Figure 1. The monopile pile head rotation is depicted in Figure 2 using the python script shipped with this file.

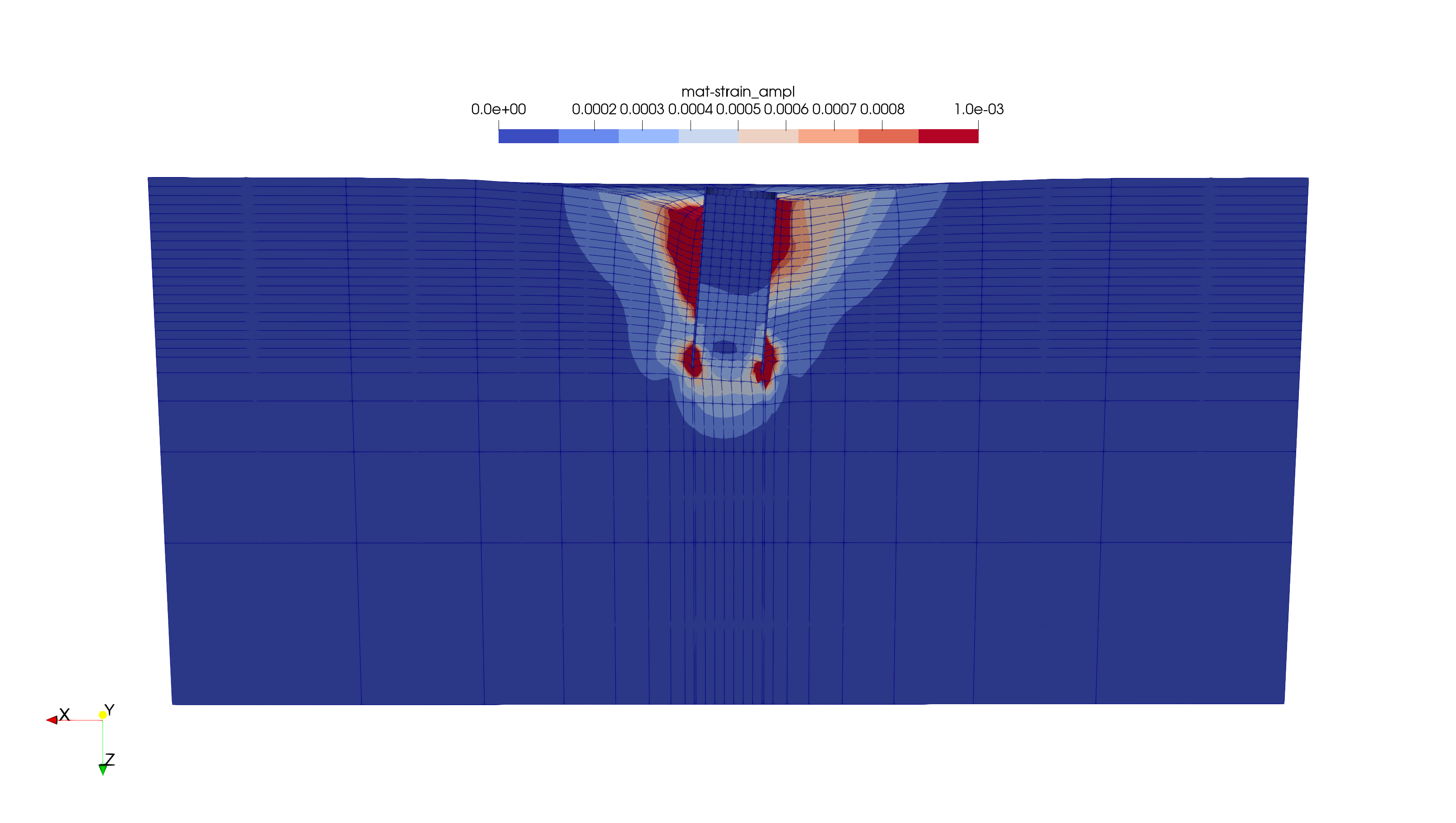figure 1 Figure 1. Field of strain amplitude and pattern of deformations at 1 million cycles (5-times enhanced)

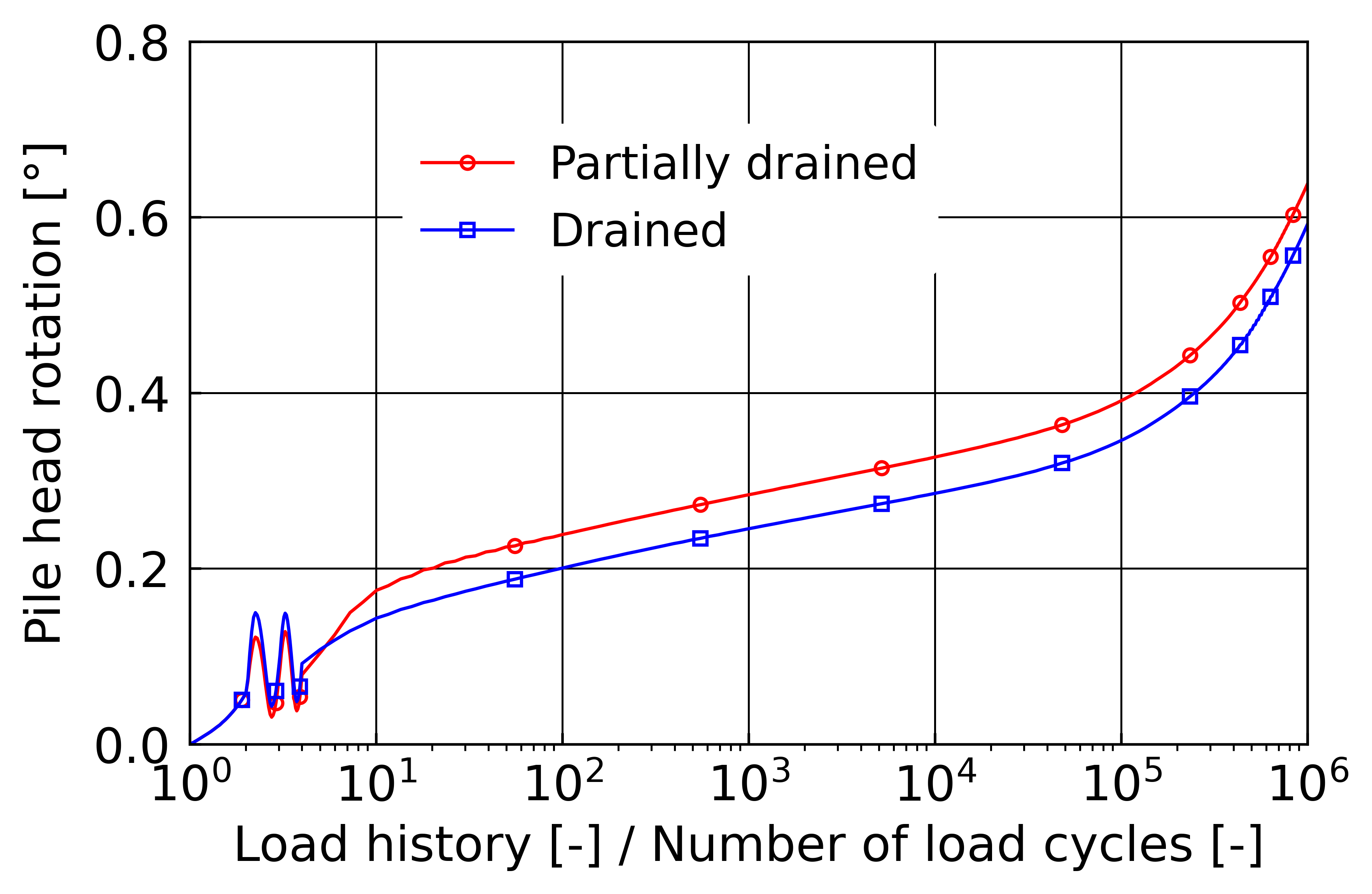figure 2 Figure 2. Pile head rotation vs. time or number of load cycles

  1. C. Taylor and P. Hood. A numerical solution of the Navier-Stokes equations using the finite element technique. Computers and Fluids, 1(1):73–100, 1973. URL: https://www.sciencedirect.com/science/article/pii/0045793073900273, doi:10.1016/0045-7930(73)90027-3. ↩