Linear Viscosity

The Linear Viscosity model introduces a viscous stress component that is proportional to the strain rate. It can be superimposed on existing constitutive models, e.g. to improve the numerical stability for very fast deformations at vanishing mean effective stress

---

Viscous Stress Formulation

The viscous stress \(\boldsymbol{\sigma}^{\text{vis}}\) is computed as:

\[ \boldsymbol{\sigma}^{\text{vis}} = \lambda \, \boldsymbol{1} \, \text{tr}(\dot{\boldsymbol{\varepsilon}}) + 2\mu \, \dot{\boldsymbol{\varepsilon}} \]

Here: - \(\dot{\boldsymbol{\varepsilon}}\) is the strain rate tensor, - \(\lambda\) and \(\mu\) are the viscous Lamé coefficients, which define the volumetric and deviatoric resistance to strain rate.

---

Pressure Dependency

Both \(\lambda\) and \(\mu\) are assumed to vary linearly with the mean effective stress \(p=\sigma_{ii}/3\) (compression is negative):

\[ \begin{aligned} \lambda(p) &= \lambda_0 + \dfrac{\lambda_0 - \lambda_1}{p_0 - p_1} (p - p_0) \\ \mu(p) &= \mu_0 + \dfrac{\mu_0 - \mu_1}{p_0 - p_1} (p - p_0) \end{aligned} \]

where:

• \(\lambda_0\), \(\lambda_1\) and \(\mu_0\), \(\mu_1\) are material parameters (units: F/A·s),
• \(p_0\), \(p_1\) are reference pressures that define the linear dependence range.

This formulation allows the material’s viscous behaviour to become stress-dependent, as illustrated in Figure 1.

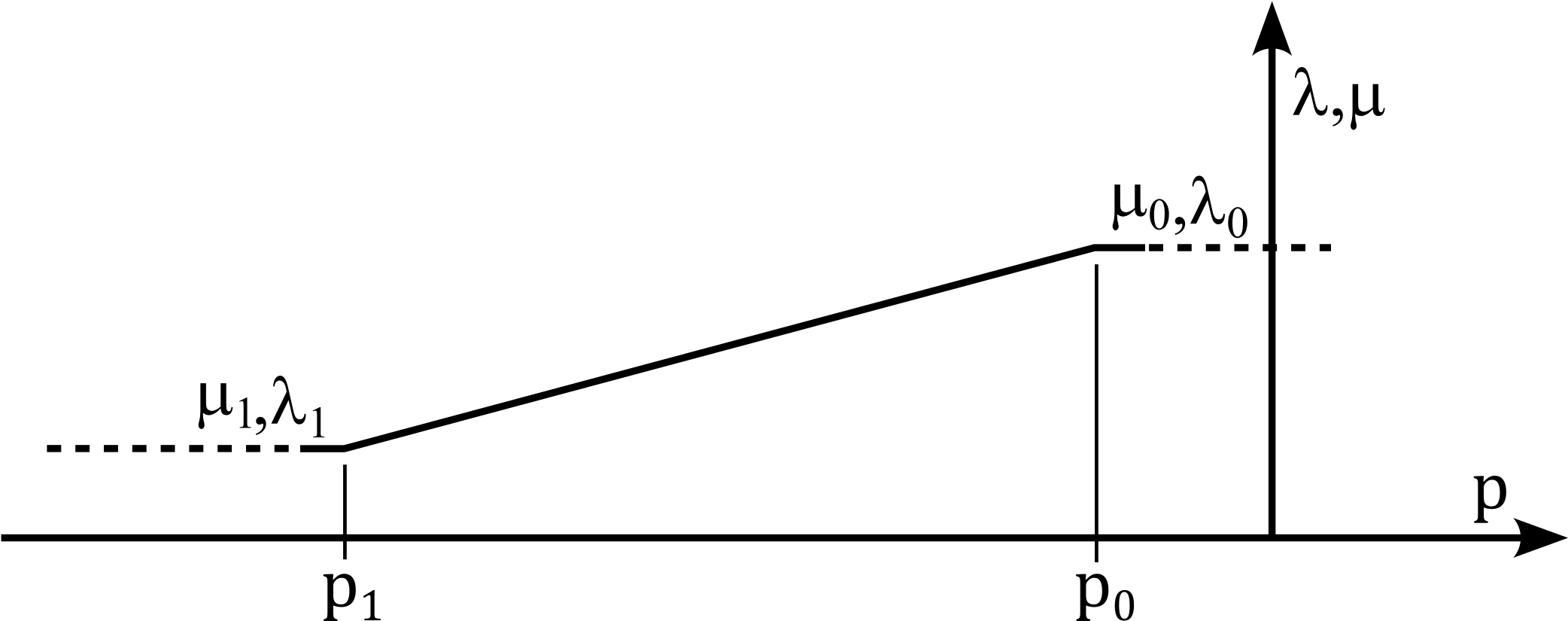
Figure 1: Pressure-dependency of viscous Lamé parameters \(\mu\) and \(\lambda\).