Skip to content

Changing the linear system solver

numgeo offers several Solvers to solve the linear system of equations that arises during Newton-Raphson iterations. In this tutorial, we'll cover:

  • How to switch from the default solver (mkl Pardiso) to another solver.
  • How your choice of solver can impact simulation runtime and scalability.

Unlike other tutorials, this one is less of a step-by-step guide and more of an informative report on a practical application. The input files are provided (download here) but won't be explained in detail.

The demonstration uses a medium-scale 3D simulation of a horizontally loaded single pile in homogeneous sand.

Problem statement

The pile considered is a hollow steel tube with a diameter of \(D = 60\) cm and a total length of 3 m, of which 2 m are embedded in dense sand. The sand used is Darmstadt sand, with an initial relative density of approximately 90 %. The material behaviour of the sand is described using the hypoplastic constitutive model with intergranular strain anisotropy (Hypo-ISA). The initial vertical stress was assumed to vary linearly with depth, computed using a dry unit weight of 1.8 m³, with an additional artificial (stabilising) surcharge of 0.5 kPa applied uniformly at the ground surface. The horizontal stresses \(\sigma_h\) were derived the Duncan et al. (1991)1 charts to account for the effect of compaction by a vibratory plate. The initial void ratio was set to \(e_0 = 0.488\). To initialise the intergranular strain framework, the intergranular strain tensor \(\boldsymbol{h}\) and the back-strain tensor \(\boldsymbol{c}\) were prescribed in a fully mobilised state in vertical direction, with \(h_{33} = -R\) and \(c_{33} = -R/2\). The interaction between soil and pile was modelled using the element-based mortar discretisation technique. The interface allows for separation in the normal direction. A friction coefficient of \(\mu = 0.38\), corresponding to \(\tan(2/3\,\varphi_c)\), was applied at the contact surface. The discretised model is depicted in Figure 1 and consists of a total of ~23,000 u8-solid-3D elements and 27,000 nodes.


Finite element model and mesh of the horizontally loaded single pile.

Changing the linear system solver

You can select the linear system solver using the *Solver keyword within a *Step definition block.

*Step, name = loading
*Static
1e-2, 1, 1e-3, 5e-2
*Solver, <Solver settings>
...
*End Step

The sub-keyword <Solver settings> depends on the Solver. Here, we'll switch from the default *Solver, Pardiso solver to MUMPS and also explore how to use an external solver.

MUMPS solver

First, we'll look at MUMPS solver. Like PARDISO, MUMPS is a robust direct solver suitable for most simulations.

To use it, simply add the following line to your step definition:

*Solver, MUMPS

No other settings are required. numgeo uses a shared-memory (OpenMP) version of MUMPS, and you can control the number of threads with the ncpus=... command line argument when you run your simulation.

External solver

numgeo also lets you connect your own solver using the *Solver, external command. This is useful for integrating third-party or custom-built solvers. See also the Reference manual.

Here's how it works:

  1. During each Newton-Raphson iteration, numgeo writes the assembled system matrix (in CSR and COO formats) and the right-hand-side vector to files.
  2. numgeo then calls the external program you specified. This program must read the files, solve the system of equations, and write the solution vector to an output file.
  3. Finally, numgeo reads the solution file and continues the analysis.

The user is responsible for providing this external program. For this tutorial, we'll use numgeo-mumps-mpi, an MPI-parallelized version of MUMPS included with numgeo releases.

To use it, we specify the executable name with the exe keyword. We also set the number of MPI processes and OpenMP threads.

*Solver, external, exe=$numgeo-mumps-mpi$, mpi=8, omp=1

This tells numgeo to execute the following command in the background:

set OMP_NUM_THREADS=1
mpiexec -n 8 numgeo-mumps-mpi <filename>

where <filename> is the base name for your simulation's output files.

Performance comparison

How does the choice of solver affect performance, and how well do the solvers scale with more CPUs?

The simulations were run using the default PARDISO solver and the built-in MUMPS solver on 4, 8, 12, and 16 CPUs.

Figure 2 shows the total simulation time from start to finish. For this specific problem, MUMPS is consistently faster than PARDISO. The total time includes three computationally expensive parts: element assembly (evaluating the material model), contact assembly, and solving the linear system. The plot therefore reflects the scalability of the entire process, not just the solver.


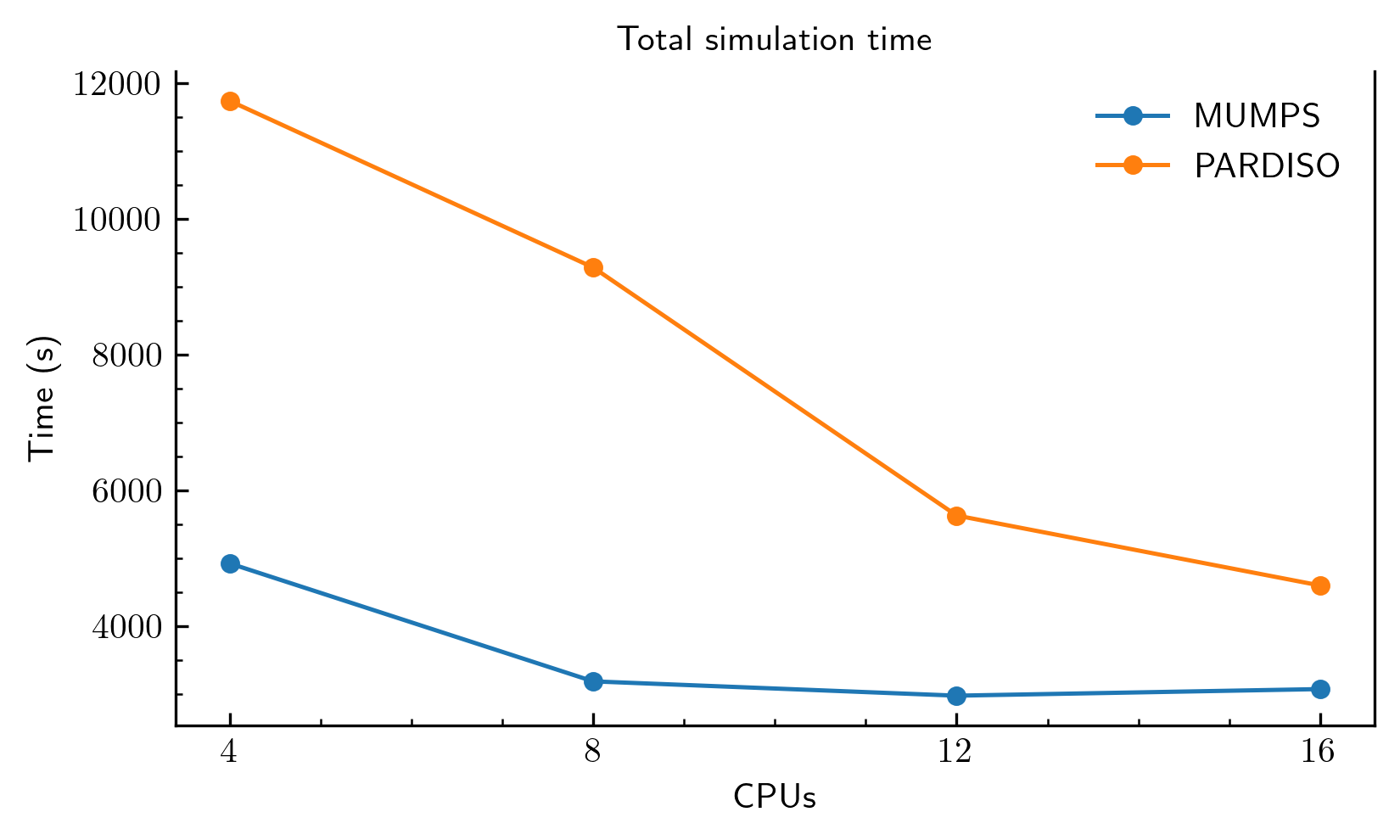
Figure 2: Total simulation time using MUMPS and PARDISO solvers with an increasing number of CPUs.

To isolate the solver performance, Figure 3 shows only the time spent solving the linear system of equations. The dashed lines show the absolute time (right axis), while the solid orange line shows the MUMPS solver time relative to PARDISO (left axis).

This confirms that the MUMPS solver itself is significantly faster for this problem, taking only 25-50% of the time that PARDISO requires. Both solvers show good scalability, with the solution time decreasing as more CPUs are added.


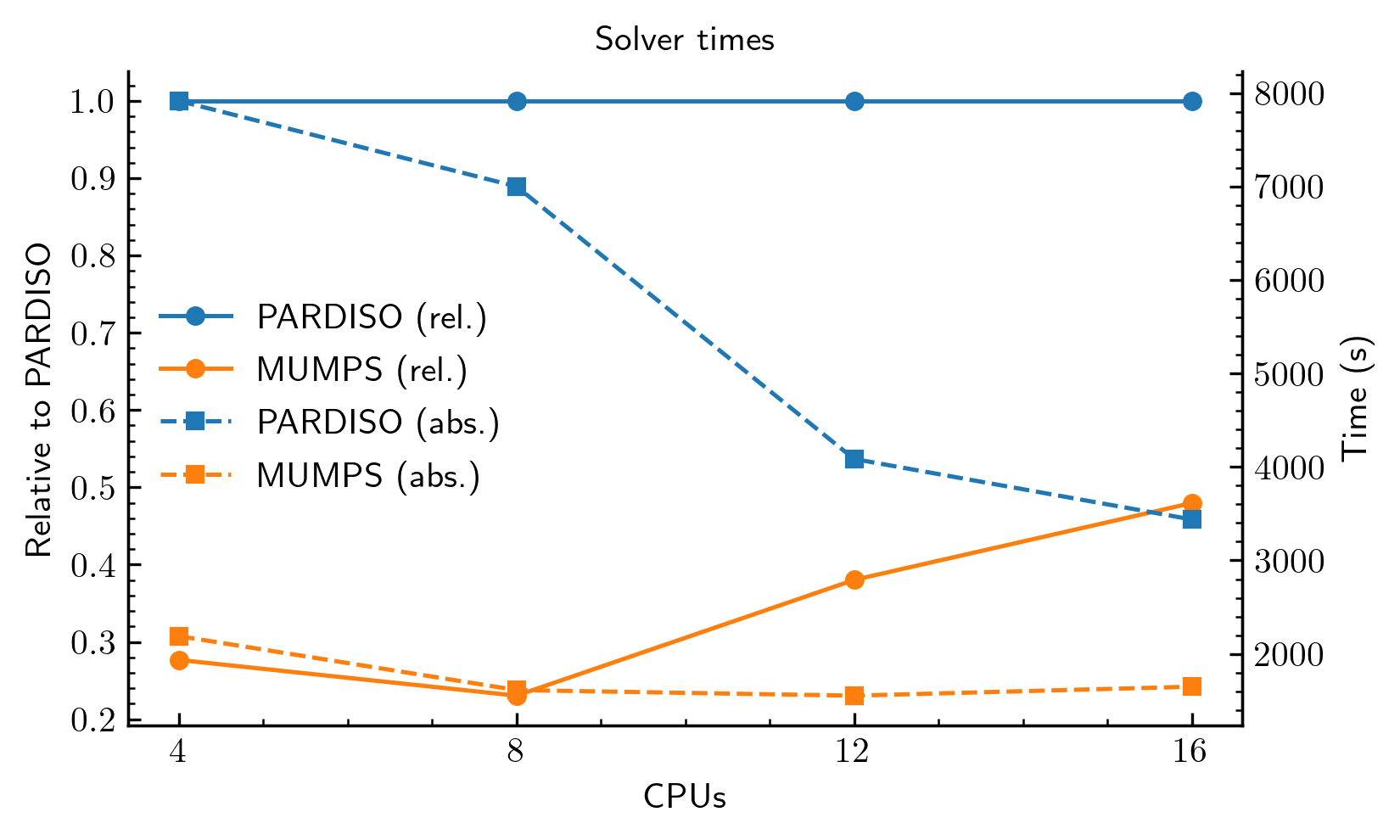
Figure 3: Solver-specific performance. Dashed lines show absolute time in seconds (right axis). Solid lines show time relative to PARDISO (left axis).

Conclusion & Key Takeaways

Based on this analysis, here are the main conclusions:

  • Solver choice matters. For this problem, switching from the default PARDISO to MUMPS resulted in a significant reduction in total simulation time.

  • MUMPS was faster. The MUMPS solver consistently outperformed PARDISO in both total simulation time and isolated solver time.

  • Scaling is important. Both solvers scaled well with an increasing number of CPUs, but the performance gains began to diminish after 8-12 cores for this specific problem size.

While PARDISO is a robust and excellent general-purpose default, it's worth experimenting with other solvers like MUMPS, as they may offer superior performance for your specific type of analysis.

  1. J. M. Duncan, G. W. Williams, A. L. Sehn, and R. B. Seed. Estimation Earth Pressures due to Compaction. Journal of Geotechnical Engineering, 117(12):1833–1847, 12 1991. doi:10.1061/(ASCE)0733-9410(1991)117:12(1833). ↩