Logistic fit
Governing Equation
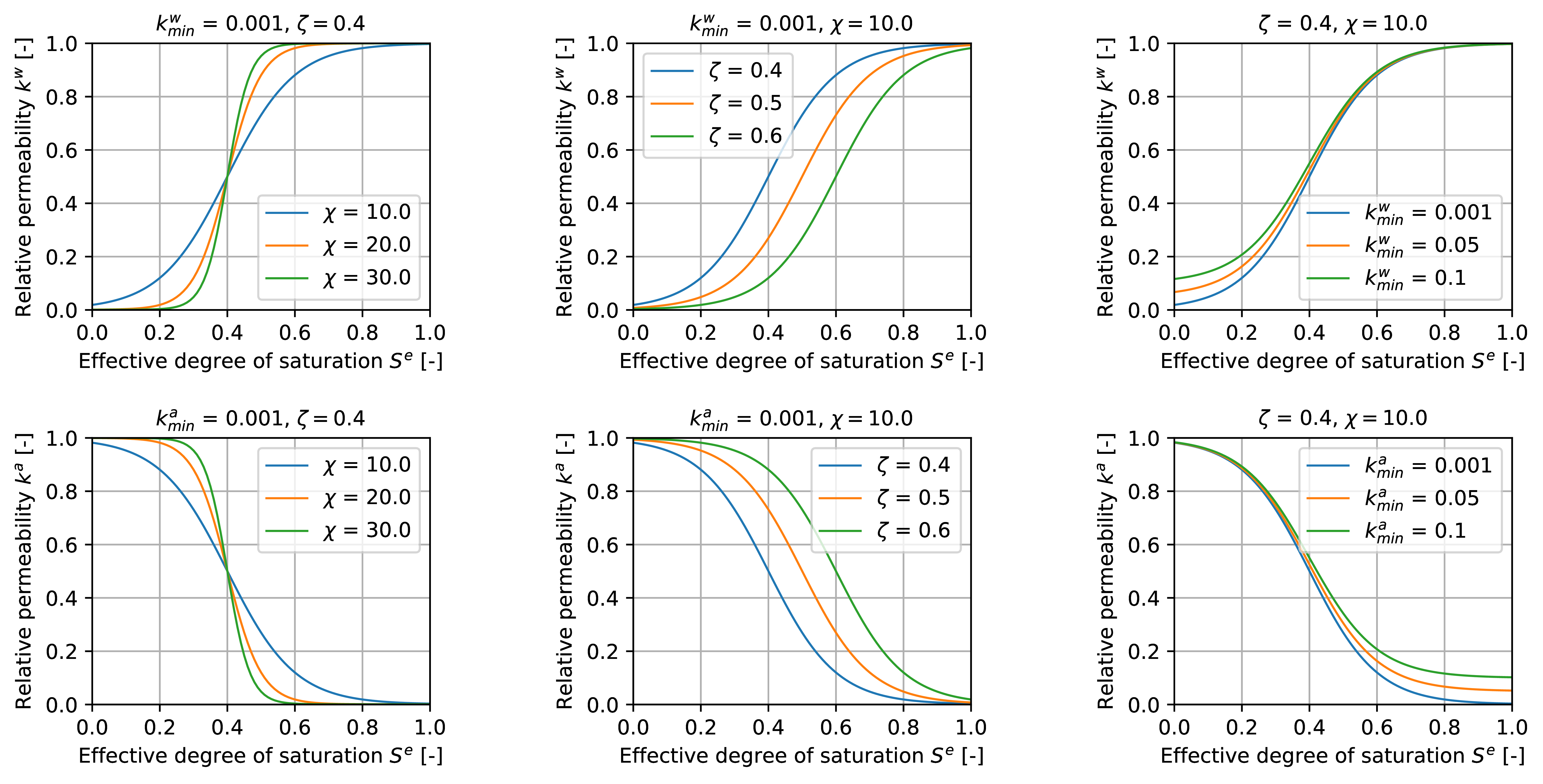
In addition to the previously introduced constitutive models for the relative permeability, we included a logistic fit function to capture the saturation dependence of the hydraulic conductivity. Note that this approach is pure curve fitting and has no physical interpretation. The relative permeability function of the pore water and pore air read \(\beta= \{w,a\}\):
\[\begin{equation*} \label{eq:rel_perm_logistic}
k^{\beta} = \frac{1-k^\beta_{min}}{1+e^{\chi^\beta(S^e-\zeta)} } + k^\beta_{min} ~~~\mbox{with:}~~ \chi^w = - \chi ~~\mbox{and}~~ \chi^a = \chi.
\end{equation*}\]
The material parameters are given in the following:
- \(k^{\beta}_{min}\) is the minimum relative permeability of pore water (\(\beta = w\)) and pore air (\(\beta = a\)), respectively.
- \(\chi\) and \(\zeta\) are curve fitting parameters.
The development of relative permeability \(k^\beta\) with effective degree of saturation \(S^e\) is presented here:
Jacobian Contribution
The contributions of to the Jacobian read:
\[\begin{align*}
\frac{\partial k^w}{\partial S^e} &= \left(1-k^w_{min}\right) \chi \frac{e^{-\chi(S^e-\zeta)}}{\left( 1+e^{-\chi(S^e-\zeta)} \right)^2}, \label{eq:rel_perm_deriv_logistic_1} \\
\frac{\partial k^a}{\partial S^e} &= -\left(1-k^a_{min}\right) \chi \frac{e^{\chi(S^e-\zeta)}}{\left( 1+e^{\chi(S^e-\zeta)} \right)^2}. \label{eq:rel_perm_deriv_logistic_2}
\end{align*}\]
-
Reference manual