Gallipoli et al. (2003)
The Gallipoli model1 extends the van Genuchten formulation2 by explicitly accounting for the influence of the void ratio on the Soil–Water Retention Curve (SWRC).
To validate our implementation, we reproduce the sensitivity of the model response to varying void ratios and compare it with the reference results reported by Gallipoli et al. (2003)1. The material parameters correspond to compacted Speswhite kaolin and are summarised below.
| \(\phi\) (kPa\(^{-1}\)) | \(\psi\) | \(n\) | \(m\) | \(S_r\) |
|---|---|---|---|---|
| 0.02691 | 8.433 | 3.746 | 0.03586 | 0.0 |
The simulations consider an undeformable porous medium with different initial void ratios of \(e_0=\{0.8, 0.9, 1.0, 1.1, 1.2, 1.3\}\). The simulations are performed in a single element setting using flow-only elements. All samples start at an initial suction of \(s=-p^w=300\) kPa and are saturated in a steady-state analysis by prescribing the pore water pressure \(p^w\) at all nodes. A linear increase of pore water pressure from -300 kPa to 0 kPa is considered.
Figure 1 compares the SWRCs obtained with numgeo against the reference curves from Gallipoli et al. (2003)1. The agreement is excellent across the full range of void ratios and suctions considered.
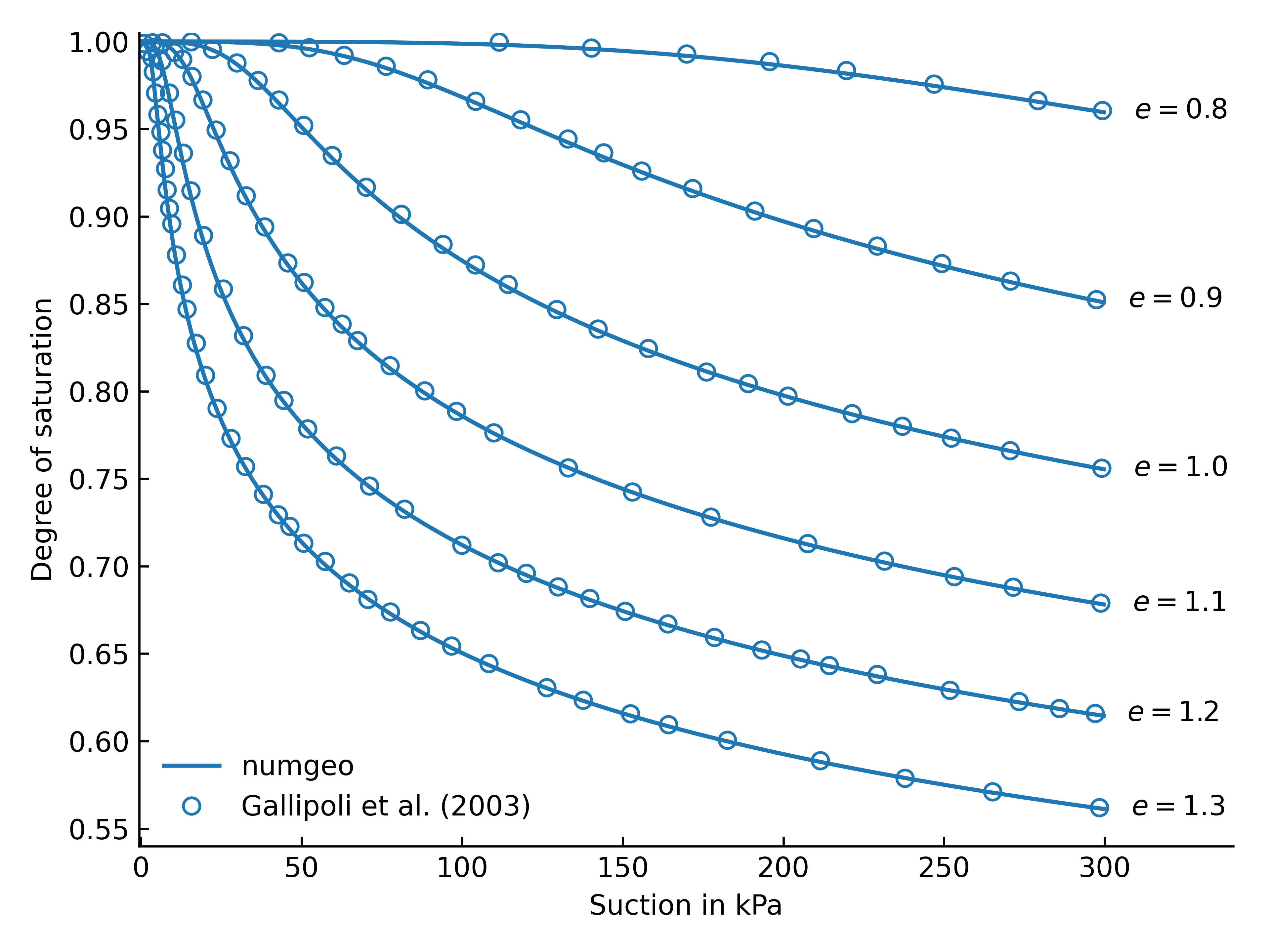Figure 1: Comparison of numgeo predictions with the reference SWRCs for varying initial void ratios \(e_0\).
Input files
The input files for the benchmark simulations and python script to generate the plot can be downloaded here.
-
D. Gallipoli, S. J. Wheeler, and M. Karstunen. Modelling the variation of degree of saturation in a deformable unsaturated soil. Géotechnique, 53(1):105–112, 2003-02. doi:10.1680/geot.2003.53.1.105. ↩↩↩
-
M. Th. van Genuchten. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal, 44(5):892–898, 1980. URL: http://doi.wiley.com/10.2136/sssaj1980.03615995004400050002x (visited on 2022-04-07), doi:10.2136/sssaj1980.03615995004400050002x. ↩