Transient seepage through dam

Sample numgeo input file

The input files can be downloaded here.

The aim of this tutorial is to demonstrate the water flow within the earth dam embankment. The flow originates from the left side of the dam. The position of the phreatic level depends upon the river water level, which progressively rises linearly before getting constant over time. Simulations were conducted for two dam geometries: one without a core and the other with a core.

Theory

Dam without a Core (Uncored Dam):

Definition: A dam without a core lacks an impermeable barrier within its structure. The entire dam body is usually made of non-cohesive materials, such as earth and rock, without a specifically designed impermeable core.

Considerations: The absence of a core means that the dam relies on the inherent properties of the materials used in its construction to resist seepage. The suitability of the foundation and construction materials becomes crucial in preventing excessive seepage.

Dam with a Core (Core Dam):

Definition: A dam with a core includes an impermeable barrier or core within the body of the dam. This impermeable core is typically made of materials like clay, concrete, or other compacted soils that have low permeability.

Purpose: The core serves as a barrier to prevent the seepage of water through the dam. Seepage can be a significant concern, as it may lead to erosion of the dam structure and compromise its stability.

Advantages: Reduces seepage and helps maintain the water within the reservoir. Enhances the overall stability and safety of the dam.

Schematic representation of Dam embankment

Figure 1 shows the schematic representation of the earth dam embankment, where upstream of dam is at the left side. The crest of the dam embankment has a width of 8 m. Initially, the water level is at 0 m, gradually rising to 8 m over time (for 8 day, then remain constant). The vertical to horizontal slope for the dam embankment is 1:2.5.

Figure 1. Geometry of the earth dam embankment

Finite element model

The two-dimensional finite element mesh was developed using Finite element software, Abaqus (2023). The mesh of numerical model was discretised by using quadratic quad dominant elements i.e. 8-nodded quadrilateral elements and 6-nodded triangular element (Figure 2).

Figure 2. Discretized numerical model

For performing the analysis in numgeo the quadratic elements in numerical model were defined using u8p4 type element while triangular element was defined using u6p3 element.

*Element, type=u8p4
*Element, type=u6p3

Note: u6p3 is a 2D triangular shape element which have 6 nodes and 3 integration points. u8p4 is a 2D rectangular shape element which have 8 nodes and 9 integration points (for more information please refer to numgeo reference manual).

Step to step explanation of input file

Two cases were considered for performing the simulations: one without a core and the other with a core.

Case I: Dam embankment without core

An input file for simulating the flow of water in a dam embankment without a core using the linear elastic constitutive model is explained below.

First we define part of model
```
*Part, Name=Soil
*End Part
```
* Note:The entire model was generated by one part named ‘soil’. In this part a total of 5 node sets and 5 element set were defined (shown in Figure 2):

node sets
- bottom (soil.bottom)
- left_slope (soil.left_slope)
- left_water (soil.left_water)
- left (soil.left)
- right (soil.right)
element sets
- all (soil.all)
- core (soil.core)
- left_core_body (soil.left_core_body)
- right_core_body (soil.right_core_body)
- subsoil (soil.subsoil)
Next we define assembly and instance
```
*Assembly
*Instance, Name=Soil, Part = Soil
*Include = mesh_1
*End Instance
*End Assembly
```
Note: “Include=mesh_1” command is used to include the mesh file (which was develpoed using Abaqus and can be downloaded from input files) in the input file

Next we define solid sections

This section outlines the definition of solid (continuum) elements comprising the dam embankment

*Solid Section, Elset = Soil.subsoil, Material =    mat-subsoil
*Solid Section, Elset = Soil.core, Material =   mat-fill
*Solid Section, Elset = Soil.right-core-body,   Material = mat-fill
*Solid Section, Elset = Soil.left-core-body,    Material = mat-fill

Note: In this case, since there is no core, the core material is kept the same as the fill material.

Now we define the properties of the materials

Material 1 (impervious subsoil)
```
*material, name = mat-subsoil, phases = 3
```
Note: ‘Phase = 3’ represents the three phases of soil i.e. solid, water and air

Material is defined as linear elastic model. Only two parameters are required to define linear elasticity material, i.e., modulus of elasticity (E) and Poisson's ratio (ν). Linear elastic material assumes a linear relation between stress and strain. The values of E and ν are taken as 50 × 10\(^3\) and 0.3, respectively. The subsoil is impervious; therefore, the permeability was assumed to be very low, 1×10\(^{-25}\) m/s.
```
*mechanical = Linear_Elasticity
50d3, 0.3
*Density
2.66, 1.0, 1d-3
*Bulk modulus
1d5,100.0
*Dynamic viscosity
1d-6, 1d-8
*Permeability = isotropic
0.1d-24
*Hydraulic= van Genuchten, swr=0.07391
1.12,1.335
*Jacobian = smoothed
*Relative permeability = van Genuchten
1d-4, 1d-4, 1.073
*Bishop effective stress = saturation
```
Note: For saturation-suction relations Van Genuchten equation (Van Genuchten 1980) were used. The parameters required for defining the equations are α and n (1.12 and 1.335) which was selected through curve fitting as shown in Figure 3.

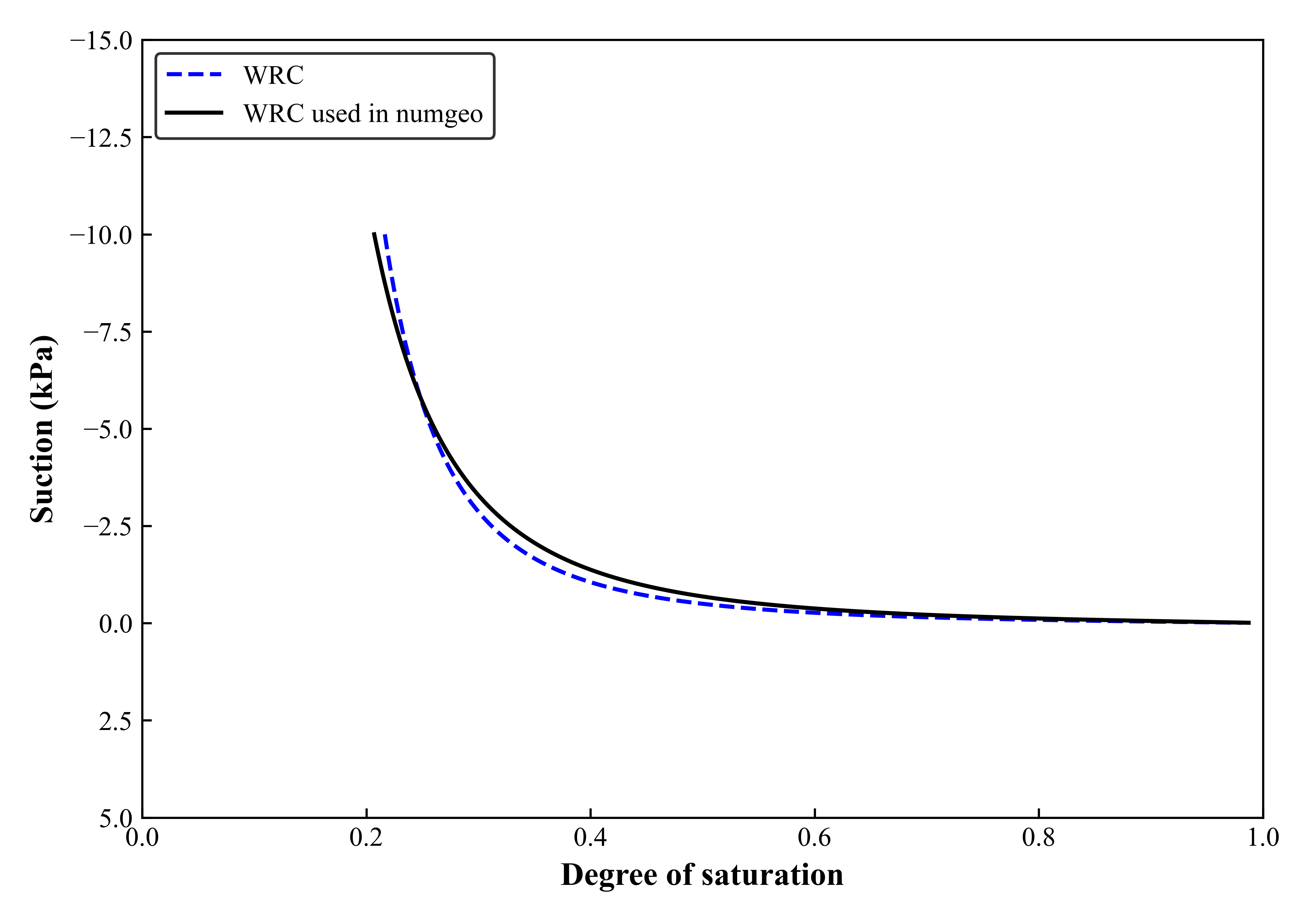
Figure 3 Suction Saturation relation for subsoil.

Material 2 (fill)
```
*material, name = mat-fill, phases = 3
*mechanical = Linear_Elasticity
25d3, 0.3
*Density
2.66, 1.0,1d-3
*Bulk modulus
1d5, 100.
*Dynamic viscosity
1d-6, 1d-8
*Permeability = isotropic
1d-12
*Hydraulic= van Genuchten, swr=0.1047
18.5, 1.243
*Jacobian = smoothed
*Relative permeability = van Genuchten
1d-4, 1d-4, 1.521
*Bishop effective stress = saturation
```
Note: For saturation-suction relations Van Genuchten equation (Van Genuchten 1980) were used. The parameters required for defining the equations are α and n (18.5 and 1.234) which was selected through curve fitting as shown in Figure 4.

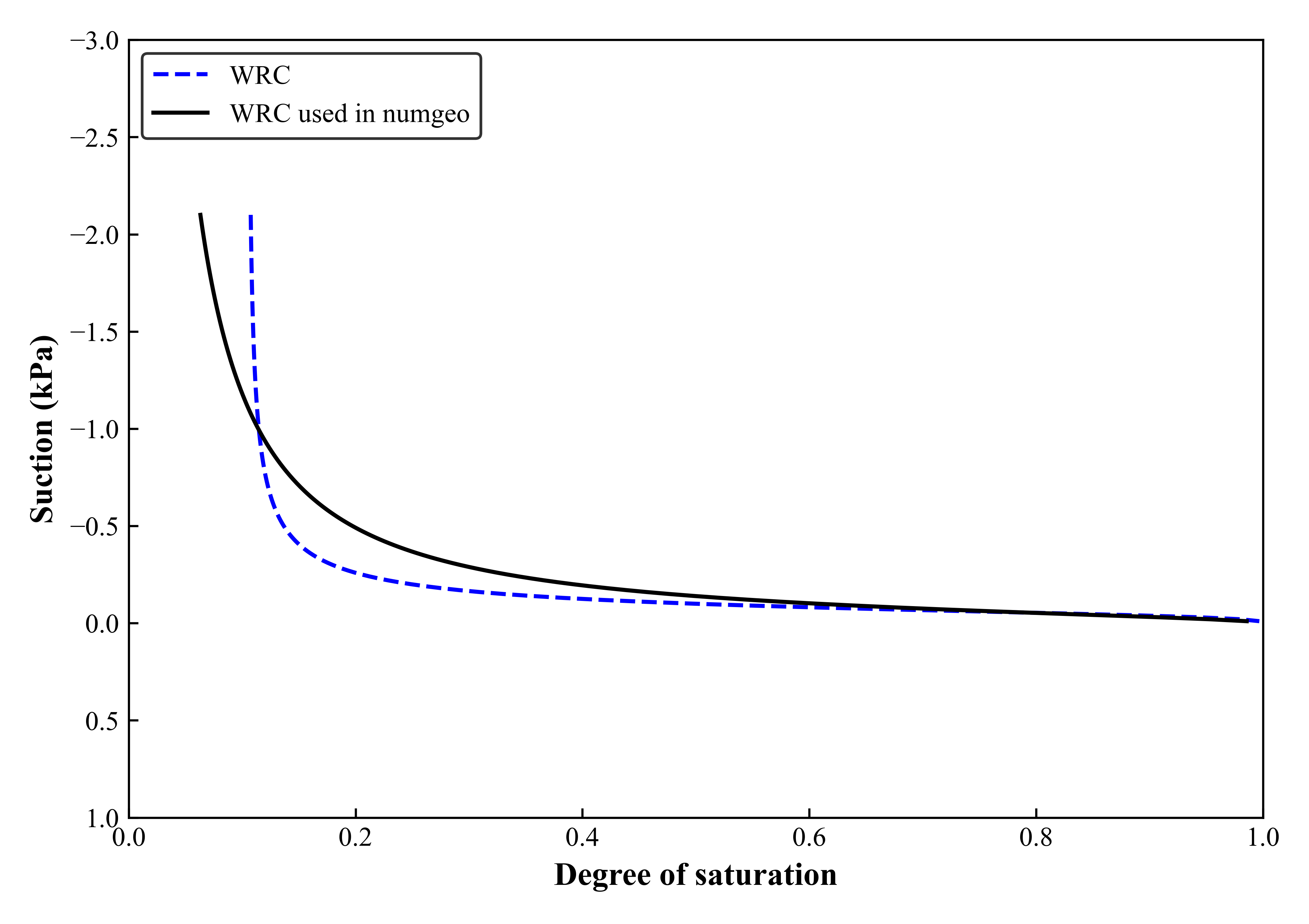
Figure 4 Suction Saturation relation for fill.
Now we define the Initial conditions.
```
*initial conditions, type=void ratio, default
```
Note: The initial value of the void ratio is assigned at the integration points of a porous medium element. The 'Default' option is utilized to assign a specific initial void ratio to all members within a specified element set.
```
Soil.subsoil, 0.01
Soil.core, 0.5
Soil.right-core-body, 0.5 
Soil.left-core-body, 0.5 
```
Note: For creating the soil nearly impervious the value of initial void ratio was taken as 0.01. In the absence of a core, the void ratio of the core is aligned with that of the fill (0.5).
```
*initial conditions, type=stress, geostatic
```
Note: The initial value of the initial stress is assigned at the integration points of an element set. The ‘Geostatic’ option is used to assign as elevation-dependent initial stress to all members of a given element set.
```
Soil.subsoil, 2, 0, 0., 40, 0.5, 0.50
Soil.core, 2, 187, 13, 0, 0.5, 0.50
Soil.right-core-body, 2, 93.5, 13, 0, 0.5, 0.50
Soil.left-core-body, 2, 93.5, 13, 0, 0.5, 0.50
```
```
*initial conditions, tpye=pore water pressure, default
```
Note: The initial value of the pore water pressure or pore air pressure is specified at the nodes of a node set. The ‘default’ option is used to assign as elevation-dependent initial pore water pressure or initial pore air pressure.
```
Soil.subsoil, 0, 19.62, 2, 0
Soil.core, 2, 0, 13, 0
Soil.right-core-body, 2, 0, 13, 0
Soil.left-core-body, 2, 0, 13, 0
```
The initial pore water pressure and degree of saturation are shown in Figure 5. It should be noted that negative pore water pressure here represents suction because the water table is located in the subsoil.

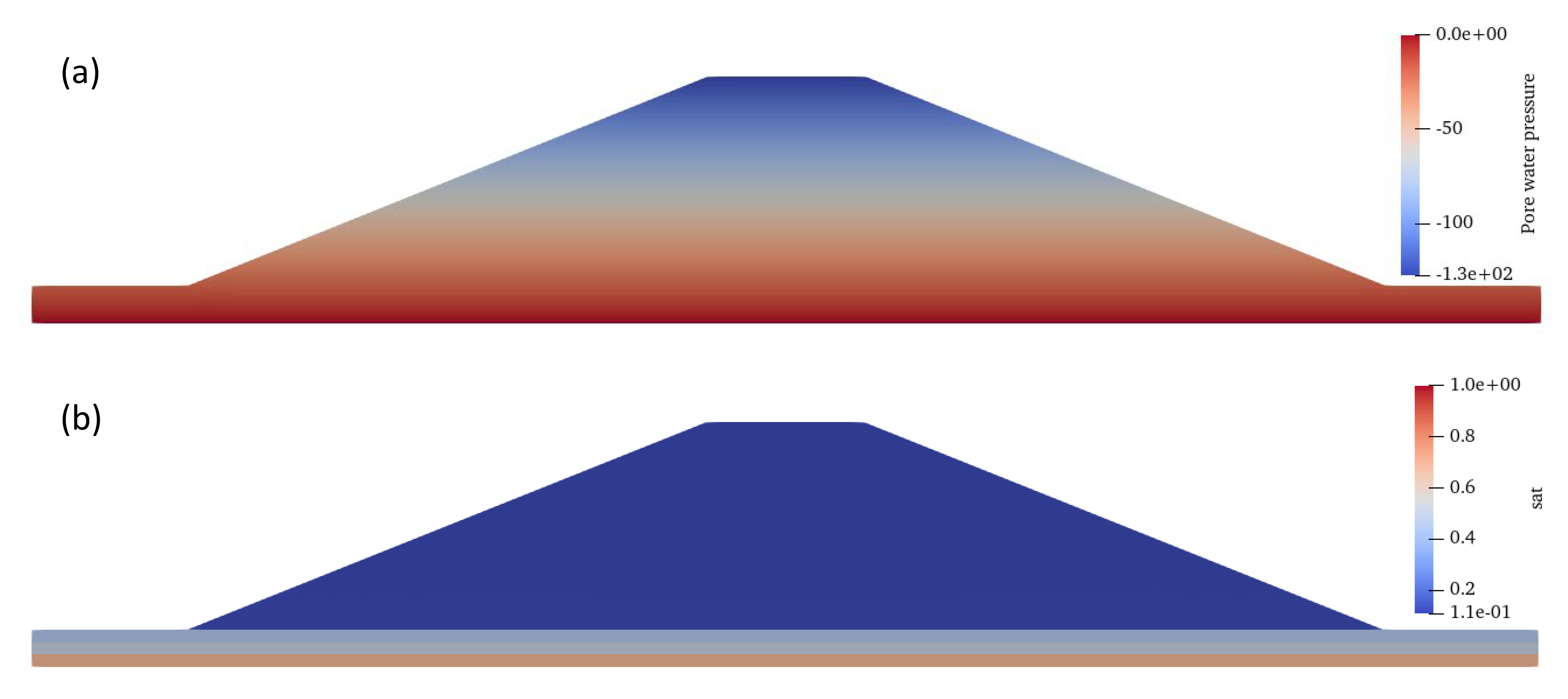
Figure 5(a) Initial pore water pressure (b) Initial degree of saturation
Now we define the geostatic step
```
*Step, name=geostatic, inc = 1
*Geostatic
```
Note: The Geostatic procedure is employed as the initial step in geotechnical analysis to apply gravity loads, and only one increment is necessary to calculate this step.
```
*BODY FORCE, INSTANT
Soil.all, GRAV, 9.81, 0, -1, 0
*Boundary,op=new
Soil.bottom, u2, 0.0d0
Soil.bottom, u1, 0.0d0
Soil.left, u1, 0.0d0
Soil.right, u1, 0.0d0
*boundary,type=hydrostatic,op=new
Soil.all, pw, 9.81, 0.001
```
Note: The base of the numerical model is fully fixed, while the lateral boundaries (left and right) are maintained in a normally fixed condition. Additionally, boundary conditions are applied to prescribe the pore water pressure for each node. The pore water pressure must exhibit a gradient equal to the specific weight of the pore water; to achieve this, the ‘hydrostatic’ command is used.
```
*Save Reaction force
Soil.all,1
```
Note: With ‘save reaction forces,’ the reaction forces at the end of the current step are stored in memory and can be used in subsequent steps.
```
*output, field, vtk, ASCII
*frequency=1
*node output, nset = Soil.all
U, V, A, pw
*element output, elset = Soil.all
S, E 
End step
```

Now we define the loading step

*Step, name=rising_step, inc = 1000000
*Transient
3, 3456.0d3, 1d-15, 10000

The water level in the reservoir is increased during the first 8 days, and then it remain at constant level (8 m) throughout the calculation. Therefore, the water supply at the upstream of the dam is simulated using a transient step.
```
*BODY FORCE, INSTANT
Soil.all, GRAV, 9.81, 0, -1, 0
*boundary, op=new
Soil.all, u1, 0.0d0
Soil.all, u2, 0.0d0
*Uboundary
soil.left-water, pw, 1
soil.left-slope, pw, 1
```
Important Simulating the increase in water level involves prescribing pore water pressure equivalent to the hydrostatic water pressure acting on the upstream slope of the dam. Because pore water pressures along the upstream slope not only vary with time but also depend on their location in space, a user-defined subroutine is employed to prescribe the pore water pressure. The code for the user-defined condition is provided below. This user-defined subroutine is a separate file and must not be included in the input file.

subroutine user_boundary_conditions(dof,inode,istep,time,coords,bc_value) &
  bind(c,name='user_boundary_conditions')
  use, intrinsic :: iso_c_binding
  implicit none
  character(c_char)           , intent(in)    :: dof          !! degree of freedomn for which the boundary condition is defined
  integer(c_int)              , intent(in)    :: inode        !! node label
  integer(c_int)              , intent(in)    :: istep        !! step label
  real(c_double)              , intent(in)    :: time         !! step time
  real(c_double), dimension(3), intent(in)    :: coords       !! coordinates of the integration point
  real(c_double), dimension(3), intent(inout) :: bc_value     !! initial stress
  real(c_double) :: gammaW, initial_suction, final_pw, rising_time, m, suction0, final_water_height
  integer :: raising_step
  gammaW = 9.81d0
  suction0 = 0.0d0
  rising_time = 8.0d0 * 24.0d0 * 60.0d0 * 60.0d0
  final_water_height = 10.0d0
  raising_step = 2
  if(istep == raising_step) then
    initial_suction = -suction0 - (coords(2))*gammaW
    final_pw = (final_water_height-coords(2)) * gammaW
    if (time < rising_time) then
        m = (final_pw-initial_suction)/rising_time
        bc_value(1) = initial_suction + m*time
    else
        bc_value(1) = final_pw
    end if
  endif   
end subroutine user_boundary_conditions

In the end we define the output

*Output, field, vtk, ascii
*frequency=2000
*Node output, nset=dam.all
u, pw
*Element output, elset=dam.all
S, E, sat_eff, darcy_w1, darcy_w2, sat
**
*End Step
**
*End Input

Note: The numgeo input file is case-insensitive - use upper and lower cases as you wish.

Results for Case I

After conducting the simulation the position of phreatic surface was recorded with respect to time. The phreatic surface can be defined where the pore water pressure is zero or saturation is equal to one. The evaluation of the phreatic surface was performed by using the post processing software Paraview (Ahrens et al. 2005). The contours for zero pore water pressure can be observed in Figure 6, while Figures 7 shows the variations in pore water pressure over time. It was clearly observed that water is seeping into the embankment, leading to an increase in both pore water pressure.

Figure 6. Contours of phreatic surface for different times of the simulation

Figure 7. Pore water pressure for different times of the simulation

The degree of saturation is compared with the simulation conducted in Plaxis2D. It was observed that the numgeo results are in good agreement with the Plaxis2D results (Figure 8).

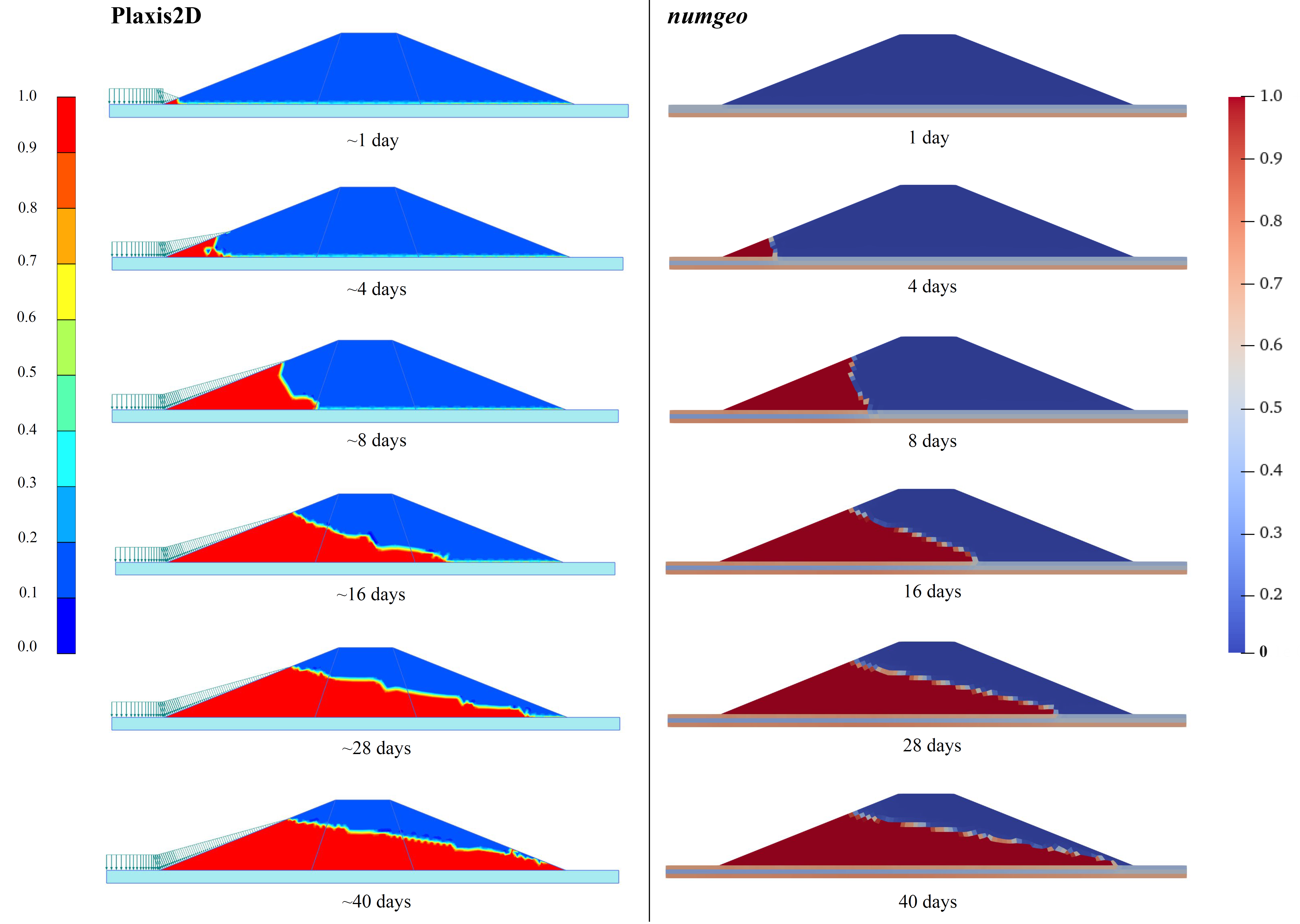
Figure 8. Comparison between numgeo and Plaxis2D for the degree of saturation at different times during the simulation.

Case II: Dam embankment with core

The input file for simulating the flow through the dam embankment with a core is an extension of the previous case with added details related to the core. Note: The only difference in the simulation is that there is additional material representing the core of a dam.

Material 3 (core)

*material, name = mat-core, phases = 3
*mechanical = Linear_Elasticity
** E, nu
1.5d3, 0.35
*Density
2.66, 1.0, 1d-3
*Bulk modulus
1d5,100.
*Permeability = isotropic
0.1d-16
*Hydraulic= van Genuchten, swr=0.1789
0.8, 1.067
*Jacobian = smoothed
*Relative permeability = van Genuchten
1d-4, 1d-4, 1.073
*Bishop effective stress = saturation
*Dynamic viscosity
1d-6, 1d-8

Note: For saturation-suction relations Van Genuchten equation (Van Genuchten 1980) were used. The parameters required for defining the equations are α and n (0.8 and 1.067) which was selected through curve fitting as shown in Figure 9.

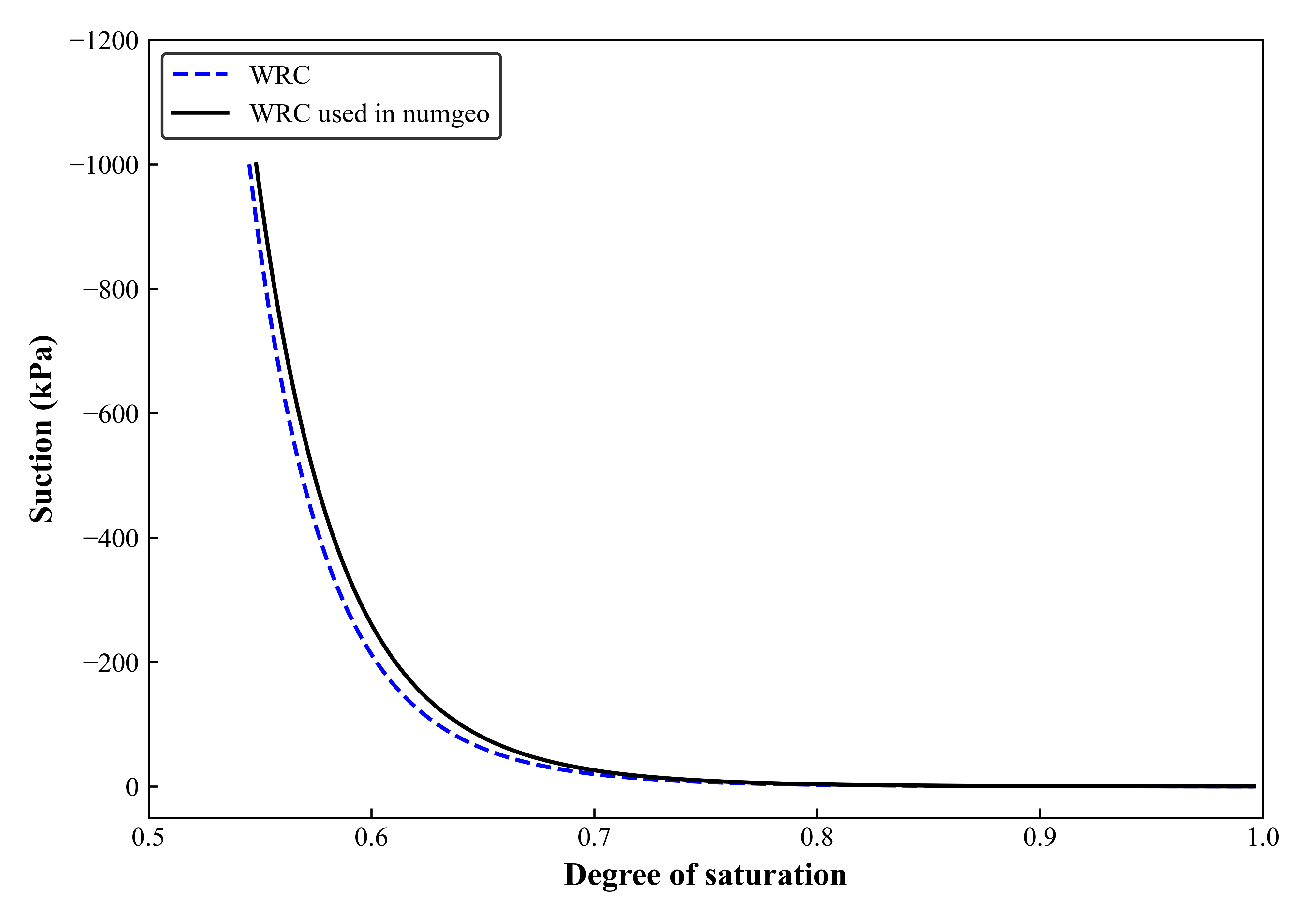
Figure 9. Suction-saturation relation for core

Please note that all the other procedure remains the same as per case I.

Results for Case II

After conducting the simulation the position of phreatic surface was recorded with respect to time.

Figure 10. Contours of phreatic surface for different times of the simulation

Figure 11. Pore water pressure for different times of the simulation

The degree of saturation is compared with the simulation conducted in Plaxis2D. It was observed that the numgeo results are in good agreement with the Plaxis2D results (Figure 12).

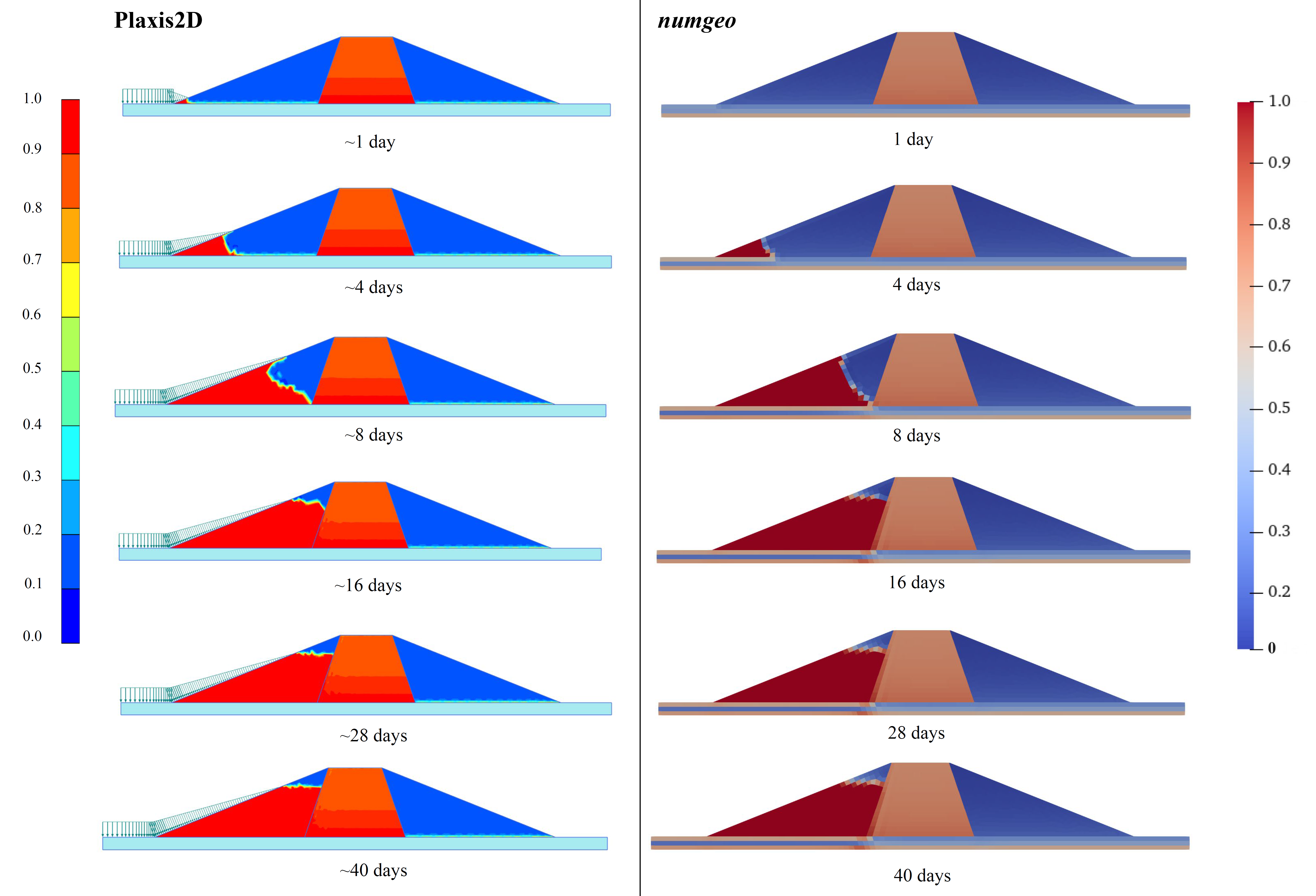
Figure 12. Comparison between numgeo and Plaxis2D for the degree of saturation at different times during the simulation.

Abaqus [Computer Software]. Dassault Systèmes. https://www.3ds.com/products-services/simulia/products/ abaqus/ ↩
Ahrens, J., Geveci, B., Law, C., Hansen, C., & Johnson, C. (2005). 36-paraview: An end-user tool for large-data visualization. The visualization handbook, 717, 50038-1. ↩
Plaxis2D 22.00.00.1733 [Computer Software]. PLAXIS B V, Netherlands. ↩
Van Genuchten, M. T. (1980). A closed‐form equation for predicting the hydraulic conductivity of unsaturated soils. Soil science society of America journal, 44(5), 892-898. ↩