Two-phase saturated porous elements with pore water pressure dof (u-p elements)

These elements are implemented for simulating the response of a two-phase solid-fluid fully coupled material, based on Biot's theory of porous medium:

• The porous medium is composed of one solid phase (e.g. soil skeleton) and one pore-fluid (e.g. water) and is assumed to be always saturated.

• Each node has 3 (4 in 3D) degrees of freedom:

  • solid displacements \(u_1\) and \(u_2\) (and \(u_3\) in 3D)
  • pore-fluid pressure \(p^w\)

• The prescribed densities are the density of the solid grains \(\rho^s\) and the pore fluid \(\rho^w\). The density of the continuum \(\rho\) is calculated based on the assigned porosity \(n\) (or void ratio):

  \[ \rho = (1-n) \cdot \rho^s + n \cdot \rho^w \]

Taylor-Hood Elements

2D Elements

Element label	Dim.	Shape	Nodes	Order	nIP*	Remarks
u4p4-sat	2D	rectangle	4	linear	4	(1), (6)
u6p3-sat	2D	triangle	6	quadratic	3	(1), (2)
u8p4-sat	2D	rectangle	8	quadratic	9	(1), (2)
u8p4-sat-red	2D	rectangle	8	quadratic	4	(2), (3)

Axisymmetric Elements

Element label	Dim.	Shape	Nodes	Order	nIP*	Remarks
u4p4-sat-ax	axisym.	rectangle	4	linear	4	(1), (6)
u6p3-sat-ax	axisym.	triangle	6	quadratic	3	(1), (2)
u8p4-sat-ax	axisym.	rectangle	8	quadratic	9	(1), (2)
u8p4-sat-ax-red	axisym.	rectangle	8	quadratic	4	(2), (3)

3D Elements

Element label	Dim.	Shape	Nodes	Order	nIP*	Remarks
u20p8-sat	3D	brick	20	quadratic	27	(1), (2), (4)
u20p8-sat-red	3D	brick	20	quadratic	8	(2), (3)
u27p8-sat	3D	brick	27	quadratic	27	(1), (2)

Stabilized first-order elements

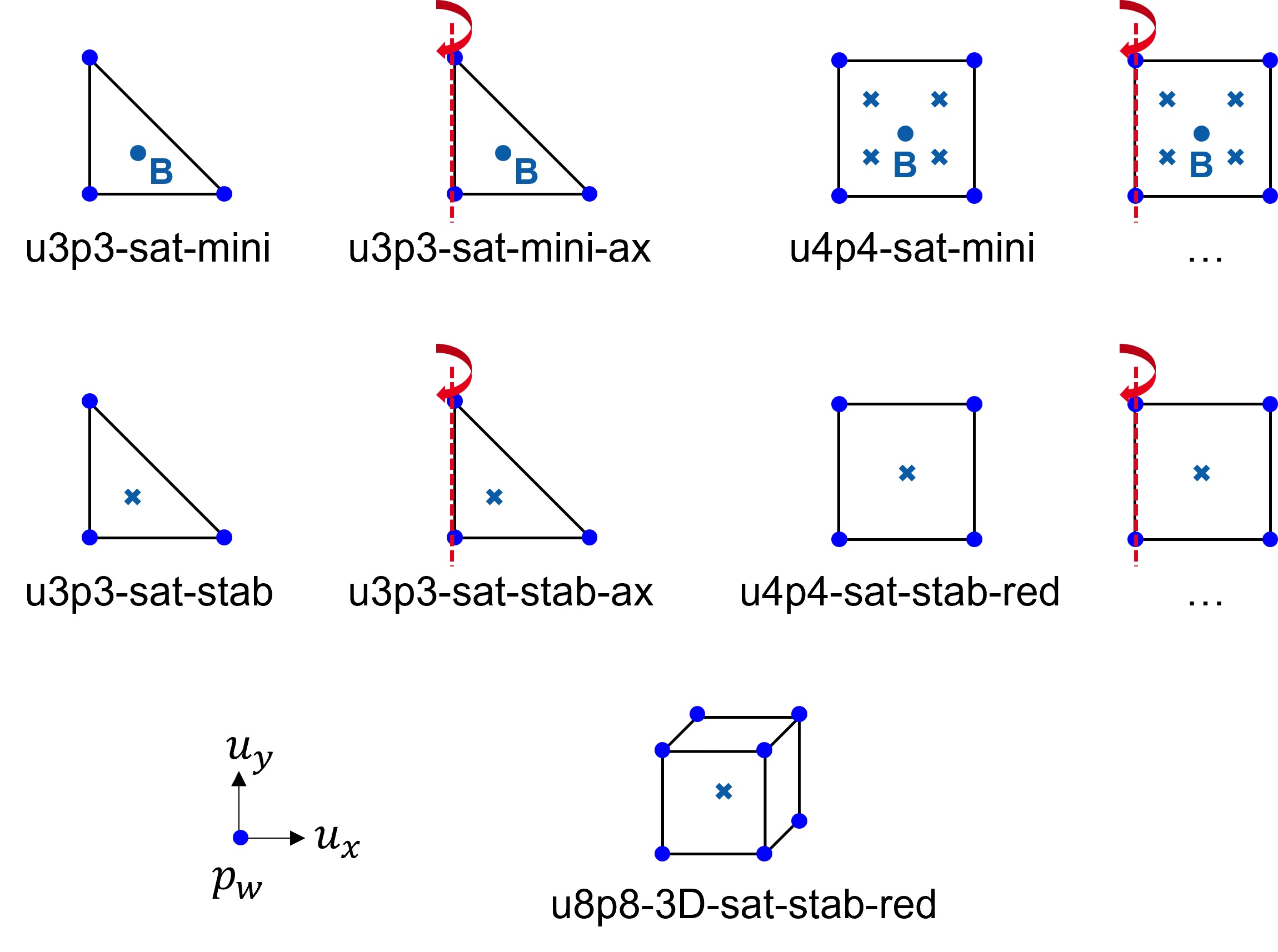
In coupled poromechanics problems, finite elements sometimes exhibit pressure oscillations especially near draining boundaries. These oscillations can be caused by (a) the incompressibility constraint and can be attributed to the violation of the LBB-condition or (b) by violation of the minimum time step criterion. The so far presented elements follow the Taylor-Hood formulation where the solid displacement is integrated using second order (quadratic) shape functions whereas the pore water pressure is integrated using first order (linear) shape functions. These elements satisfy the LBB-condition and are thus less prone to pressure oscillations. In many problems it is however beneficial to use equal order linear shape functions for both the displacement and the (pore water) pressure. In such cases, stabilization methods need to be applied, see Reference Manual. The following first-order elements are implemented in numgeo:

2D Elements

Element label	Dim.	Shape	Nodes	Order	nIP*	Remarks
u3p3-sat-mini	2D	triangle	3	linear	1	(1), (5)
u4p4-sat-mini	2D	rectangle	4	linear	4	(1), (5)
u3p3-sat-stab	2D	triangle	3	linear	1	(1), (7)
u4p4-sat-stab	2D	rectangle	4	linear	1	(3), (7)

Axisymmetric Elements

Element label	Dim.	Shape	Nodes	Order	nIP*	Remarks
u3p3-sat-mini-ax	axisym.	triangle	3	linear	1	(1), (5)
u4p4-sat-mini-ax	axisym.	rectangle	4	linear	4	(1), (5)
u3p3-sat-stab-ax	axisym.	triangle	3	linear	1	(1), (7)
u4p4-sat-stab-ax-red	axisym.	rectangle	4	linear	1	(3), (7)

3D Elements

Element label	Dim.	Shape	Nodes	Order	nIP*	Remarks
U8p8-sat-3d-stab-red	3D	brick	8	linear	1	(3), (7)

Remarks

*	nIP = number of integration points
(1)	Due to the full integration, the element will behave badly for isochoric material behavior. This shortcoming is more pronounced for linear interpolated elements and less pronounced for quadratic interpolated ones.
(2)	Taylor-Hood formulation: The solid displacements \(u\) are interpolated using quadratic shape functions, whereas the pore-fluid pressure \(p^w\) is interpolated using linear shape functions.
(3)	Reduced integration: This element does not suffer from the same locking issues as fully integrated elements.
(4)	3D-serendipity elements such as the element are not suitable for contact analysis. The option bi-quadratic can be used to automatically transform u20p8 into u27p8 elements
(5)	MINI-Elements use an additional shape ("bubble") function to satisfy the LBB-condition
(6)	Unstabilised equal order interpolated elements which do not satisfy the LBB-condition. Significant pore water pressure oscillations near the undrained limit are to be expected.
(7)	FPL-Stabilized equal order interpolated elements, stabilisation based on the Fluid Pressure Laplacian (FPL) approach

Notice that these elements require the definition of a two-phase material: (*Material,..., Phases=2) as described in *Material.

---