Three-phase porous solid elements (u-p elements)
-
Taylor-Hood elements
Elements with different order of interpolation for displacement (quadratic) and pore water pressure (linear)
-
Stabilised elements
Elements with special stabilisation techniques to satisfy the LBB condition.
These elements are implemented for simulating the response of a three-phase solid-fluid fully coupled material, based on Theory of Porous Media. The porous medium is assumed to be composed of one solid phase (e.g. the grain skeleton) and two pore-fluids (e.g. water and air). The following elements only allow to control one pore-fuild and is referred to as the "reduced" formulation.
In the "reduced" formulation, only one pore-fluid is discretized at the nodes of the element, the second pore-fluid is thus not controllable during the analysis. Each node has 3 degrees of freedom, the solid displacements \(u_1\) and \(u_2\) as well as the pore-fluid pressure \(p^w\). The capillary pressure is calculated using \(p^c=-p^w\) and the volume fraction (as well as the mass) of the second pore-fluid is derived from the saturation constraint (see Theory Manual). The following elements are available:
Stabilized equal-order elements
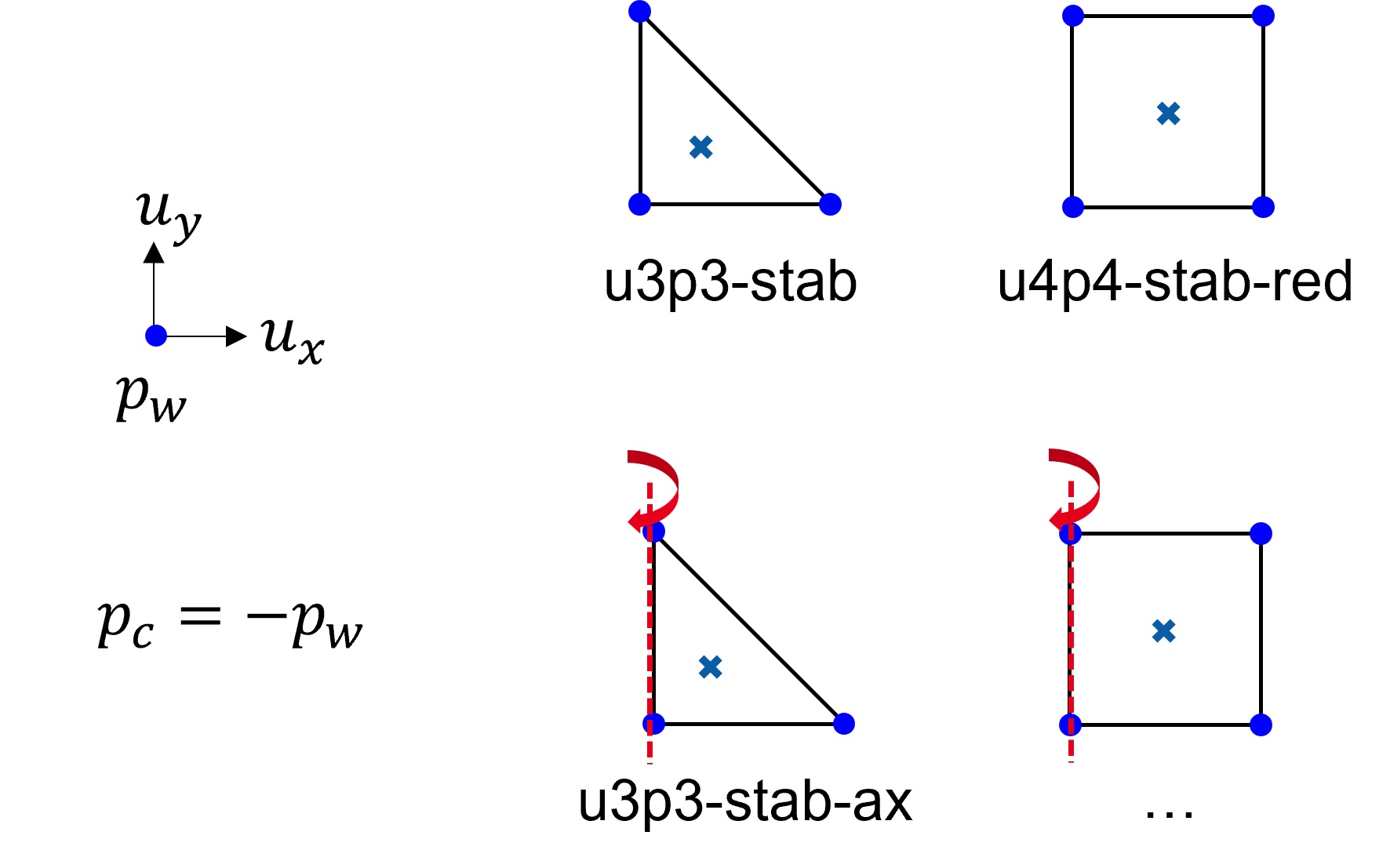
In coupled poromechanics problems, finite elements sometimes exhibit pressure oscillations especially near draining boundaries. These oscillations can be caused by (a) the incompressibility constraint and can be attributed to the violation of the LBB-condition or (b) by violation of the minimum time step criterion. The so far presented elements follow the Taylor-Hood formulation where the solid displacement is integrated using second order (quadratic) shape functions whereas the pore water pressure is integrated using first order (linear) shape functions. These elements satisfy the LBB-condition and are thus less prone to pressure oscillations. In many problems it is however beneficial to use equal order (linear or quadratic) shape functions for both the displacement and the (pore water) pressure. In such cases, stabilisation methods need to be applied, see Reference Manual. The following elements are implemented in numgeo:
2D Elements
| Element label | Dim. | Shape | Nodes | Order | nIP* | Remarks |
|---|---|---|---|---|---|---|
u3p3-stab |
2D | triangle | 3 | linear | 1 | (1), (5), (6) |
u4p4-stab-red |
2D | rectangle | 4 | linear | 1 | (4), (5), (6) , (7) |
u6p6-stab |
2D | triangle | 6 | quadratic | 3 | (1), (5) |
u8p8-stab |
2D | rectangle | 8 | quadratic | 9 | (1), (5) |
Axisymmetric Elements
| Element label | Dim. | Shape | Nodes | Order | nIP* | Remarks |
|---|---|---|---|---|---|---|
u3p3-stab-ax |
axisym. | triangle | 3 | linear | 1 | (1), (5), (6) |
u4p4-stab-ax-red |
axisym. | rectangle | 4 | linear | 1 | (4), (5), (6), (7) |
u8p8-stab-ax |
axisym. | rectangle | 4 | quadratic | 9 | (1), (5) |
u8p8-stab-ax-red |
axisym. | rectangle | 4 | quadratic | 4 | (4), (5) |
3D Elements
| Element label | Dim. | Shape | Nodes | Interpolation Order | nIP* | Remarks |
|---|---|---|---|---|---|---|
u8p8-3D-stab |
3D | brick | 8 | linear | 8 | (1), (5) |
u8p8-3D-stab-red |
3D | brick | 8 | linear | 1 | (4), (5), (6), (7) |
u20p20-stab |
3D | brick | 20 | quadratic | 27 | (1), (5) |
u20p20-stab-red |
3D | brick | 20 | quadratic | 8 | (4), (5) |
u10p10-stab |
3D | tetrahedron | 10 | quadratic | 4 | (1), (5) |
Taylor-Hood Elements
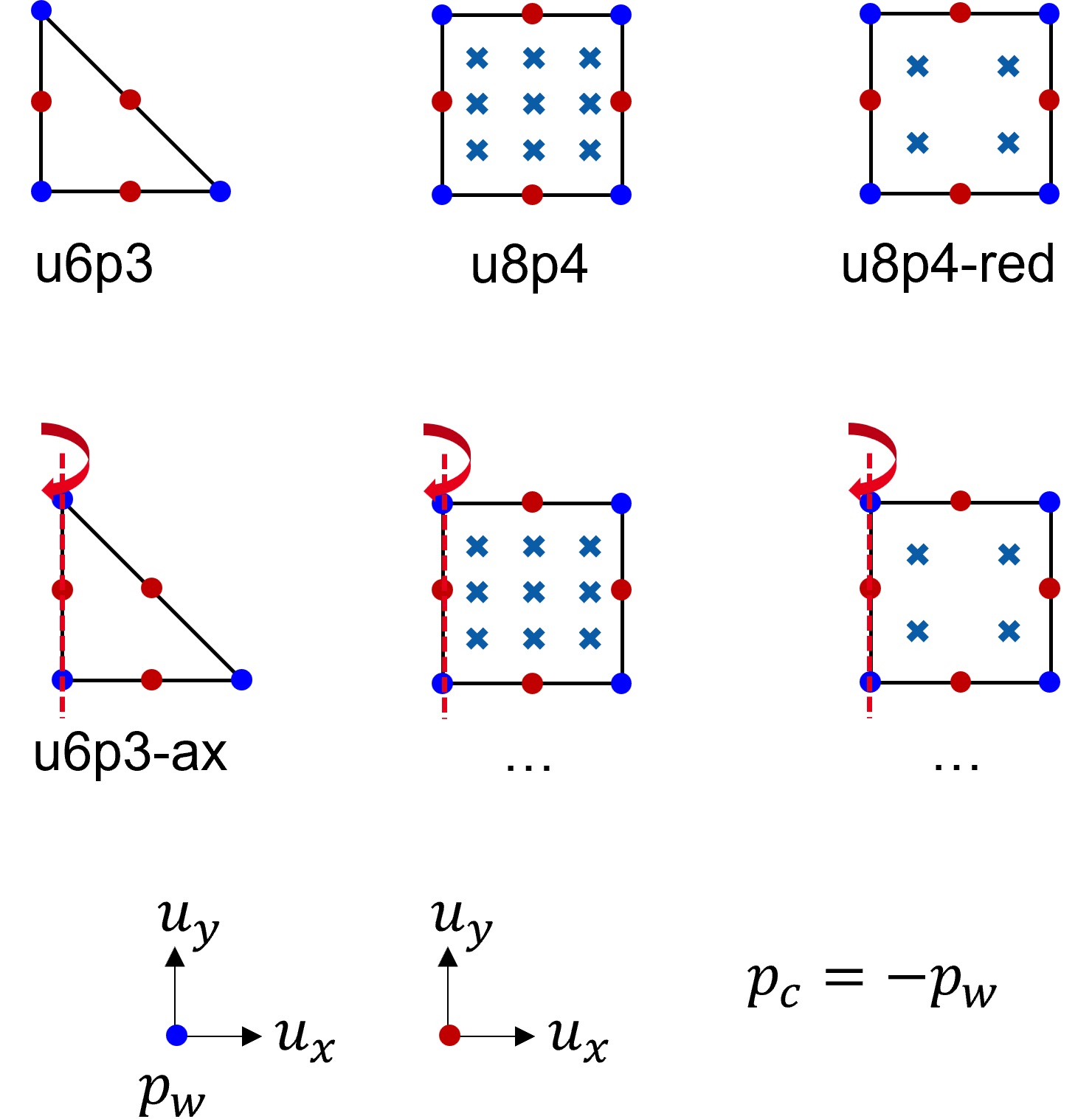
2D Elements
| Element label | Dim. | Shape | Nodes | Interpolation Order | nIP* | Remarks |
|---|---|---|---|---|---|---|
u6p3 |
2D | triangle | 6 | quadratic | 3 | (1), (2) |
u6p6 |
2D | triangle | 6 | quadratic | 3 | (1), (3) |
u8p4 |
2D | rectangle | 8 | quadratic | 9 | (1), (2) |
u8p8 |
2D | rectangle | 8 | quadratic | 9 | (1), (3) |
Axisymmetric Elements
| Element label | Dim. | Shape | Nodes | Interpolation Order | nIP* | Remarks |
|---|---|---|---|---|---|---|
u6p3-ax |
axisym. | triangle | 6 | quadratic | 3 | (1), (2) |
u8p4-ax |
axisym. | rectangle | 8 | quadratic | 9 | (1), (2) |
u8p8-ax |
axisym. | rectangle | 8 | quadratic | 9 | (1), (3) |
Remarks
| * | nIP = number of integration points |
|---|---|
| (1) | Due to the full integration, the element will behave badly for isochoric material behavior. This shortcoming is more pronounced for linear interpolated elements and less pronounced for quadratic interpolated ones. |
| (2) | Taylor-Hood formulation: The solid displacements \(u\) are interpolated using quadratic shape functions, whereas the pore-fluid pressure \(p^w\) is interpolated using linear shape functions. |
| (3) | Unstabilised equal order interpolated elements which do not satisfy the LBB-condition. Significant pore water pressure oscillations near the undrained limit are to be expected. |
| (4) | Reduced integration: This element does not suffer from the same locking issues as fully integrated elements. |
| (5) | FPL-Stabilized equal order interpolated elements, stabilisation based on the Fluid Pressure Laplacian (FPL) approach |
| (6) | This element uses 1-point reduced integration for the balance of linear momentum of the mixture and calculation of stress. For the integration of the mass balance of water and the evaluation of degree of saturation and relative permeability a 3-point or 4-point full integration scheme is used for such triangular and rectangular elements, respectively. |
| (7) | This element uses a selective augmented (or standard) integration rule for quadratic terms of the FPL stabilisation equation |
Notice that these elements require the definition of a three-phase material (*Material,..., Phases=3) as described in *Material (although only two phases are active). In addition, a saturation-suction relation and relative permeability models have to be prescribed.