User defined initial state
The input files can be downloaded here.
When using advanced constitutive models (e.g. hypoplasticity) or simulating boundary value problems with complex geometry or loading history the inbuilt functions to define initial state variables, e.g. void ratio \(e\), might not offer the required flexibility. In such cases the use of user defined initial state variables offers a possibility to initialize arbitrary state variables in a very flexible way.
For this purpose we consider the same rigid foundation on an elastic soil layer already studied in the tutorial Rigid strip footing and also used to introduce user defined material models in Section User defined material.
Warning
It is recommended to study User defined material first before continuing with this tutorial.
The model specifications are shown in Figure 1. The foundation is loaded by a distributed load along the top surface of the foundation and the settlement is studied assuming ideally drained conditions and a linearly increasing external load (\(\Delta \sigma_v(t=0 ~\text{s}) = 0\) kPa and \(\Delta \sigma_v(t=1 ~\text{s})=500\) kPa). A pressure dependent elasticity is used.
 Figure 1. Model of the rigid foundation
Figure 1. Model of the rigid foundation
The resulting vertical displacements of the top left node of the shallow foundation are reported in Figure 2.
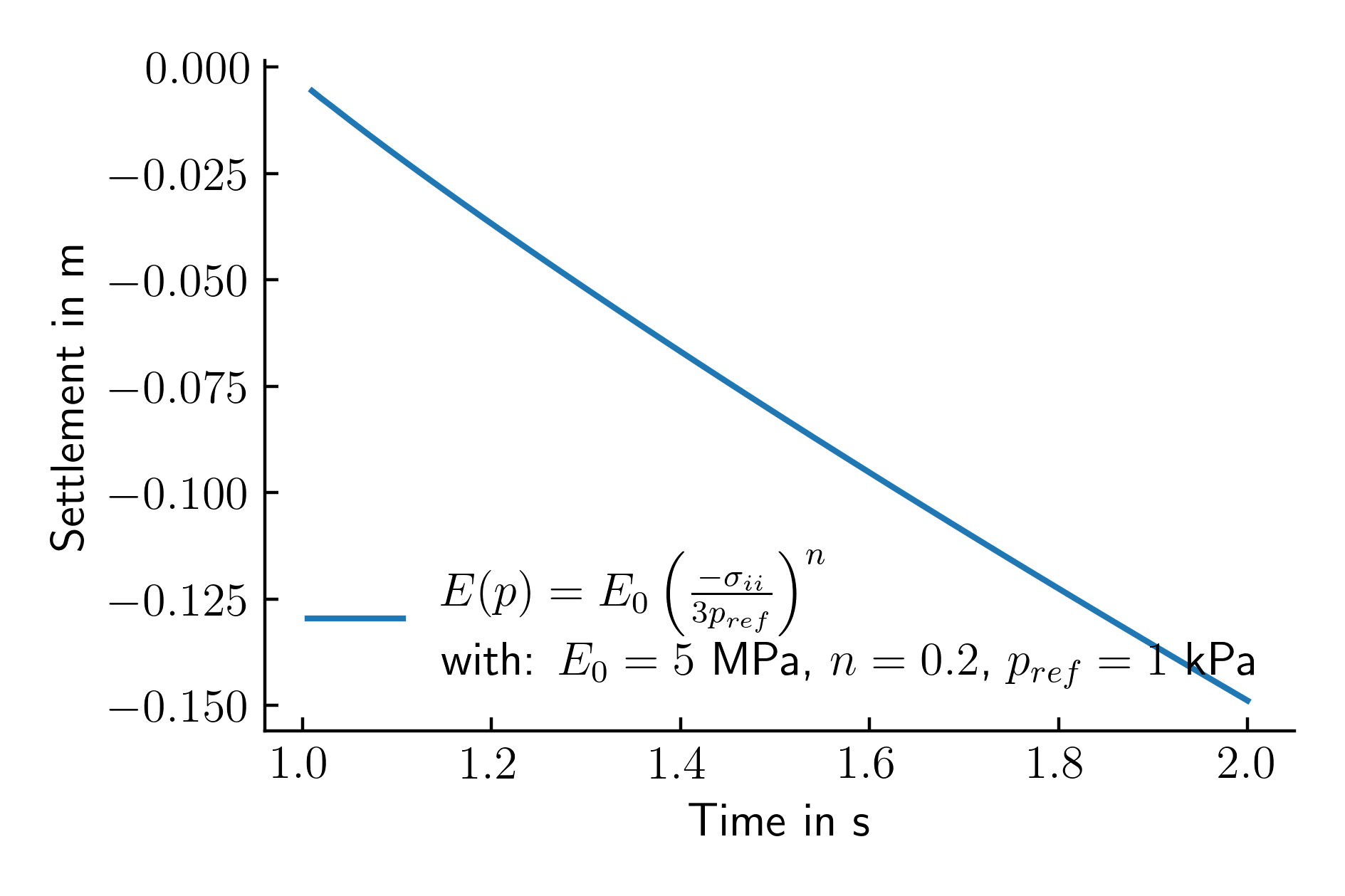
Figure 2. Settlement time history of the top left node of the shallow foundation for a linear increasing load for two different constitutive models for the soil
For the sake of this tutorial we will extend the pressure dependent model from here by a factor \(f_e\) accounting for pycnotropy (density) effects:
The relevant code snipped showing the required changes to the user material implementation presented in here is shown in the following:
subroutine user_material(material_name,nchar,ielem,igp,istep,iinc,ntens,nprops, &
nstatev,strain,dstrain,coords,time,dtime,props,statev,stress,dds_dde)
implicit none
!DEC$ ATTRIBUTES DLLEXPORT, STDCALL, REFERENCE :: user_material
...
real(8) :: EE, fe, e
...
! update void ratio and pycnotropy function
e = statev(1)
fe = (1.0d0 + e) / e
EE = E0 * fp * fe
...
statev(1) = e + (1.0d0+e)*sum(dstrain(1:3))
statev(2) = fp
statev(3) = fe
statev(4) = EE
end subroutine user_material
subroutine user_material(material_name,nchar,ielem,igp,istep,iinc,ntens,nprops,&
nstatev,strain,dstrain,coords,time,dtime,props,statev,stress,dds_dde) &
bind(c,name='user_material')
use, intrinsic :: iso_c_binding
...
real(8) :: EE, fe, e
...
! update void ratio and pycnotropy function
e = statev(1)
fe = (1.0d0 + e) / e
EE = E0 * fp * fe
...
statev(1) = e + (1.0d0+e)*sum(dstrain(1:3))
statev(2) = fp
statev(3) = fe
statev(4) = EE
end subroutine user_material
Obviously this new user defined material has an additional state variable, the void ratio \(e\), thus increasing the number of state variables to 4 (\(e, f_p, f_e, E\)). Notice that the update of the void ratio (see code for statev(1)) has to be performed in the user defined material as the state variables are private to the material model, no integration of state variables is performed by numgeo. To account for the additional state variables, change the material definition in the numgeo input file as follows:
*Material, name = soil, phases = 1
*Mechanical = user
*User properties, props=4, statev=4
5000, 0.3, 0.2, 1
*Density
2.0
To demonstrate the application of user defined initial state variables we consider a linearly increasing initial relative density with increasing depth (\(d\)) below ground surface:
For the initial distribution of void ratio \(e_0(d)\) we obtain:
where \(e_{min}\) and \(e_{max}\) are the minimum and maximum void ratio, respectively (we assume \(e_{min}=0.6\) and \(e_{max}=1.0\)). To specify the use of a user defined subroutine for the initialisation of state variables we use the following command block in the numgeo input file:
*Initial conditions, type=state variables, user
Soil.all
Note that when using the user subkeyword, the following line only contains information about the element set to which the initial conditions should be prescribed.
Next, we copy the files user_initial_state.f90 and user_initial_state.bat to the directory where we want to run the simulation. Once the files are relocated, we implement above equation into the Fortran file:
subroutine user_initial_state_variables(ie,igp,ndim,nstatev,nchar,material,coords,statev)
implicit none
!DEC$ ATTRIBUTES DLLEXPORT, STDCALL, REFERENCE :: user_initial_state_variables
integer , intent(in) :: ie !! element label
integer , intent(in) :: igp !! integration point label
integer , intent(in) :: ndim !! number of active dimensions
integer , intent(in) :: nstatev !! number of statev components
integer , intent(in) :: nchar !! length of the material name
character , intent(in) :: material(*) !! material name
real(8), dimension(3) , intent(in) :: coords !! coordinates of integration point
real(8), dimension(nstatev), intent(inout) :: statev !! initial statev
real(8) :: emin, emax, Dr0, htop
emin = 0.6d0
emax = 1.0d0
htop = 10.0d0
statev(:) = 0.0d0
Dr0 = 0.5 + 0.05*(htop-coords(2))
statev(1) = emax - Dr0 * (emax - emin)
end subroutine user_initial_state_variables
subroutine user_initial_state_variables(ie,igp,ndim,nstatev,nchar,material,coords,statev) &
bind(c,name='user_initial_state_variables')
use, intrinsic :: iso_c_binding
integer , intent(in) :: ie !! element label
integer , intent(in) :: igp !! integration point label
integer , intent(in) :: ndim !! number of active dimensions
integer , intent(in) :: nstatev !! number of statev components
integer , intent(in) :: nchar !! length of the material name
character , intent(in) :: material(*) !! material name
real(8), dimension(3) , intent(in) :: coords !! coordinates of integration point
real(8), dimension(nstatev), intent(inout) :: statev !! initial statev
real(8) :: emin, emax, Dr0, htop
emin = 0.6d0
emax = 1.0d0
htop = 10.0d0
statev(:) = 0.0d0
Dr0 = 0.5 + 0.05*(htop-coords(2))
statev(1) = emax - Dr0 * (emax - emin)
end subroutine user_initial_state_variables
The resulting initial distribution of the void ratio is given in Figure 3 showing clearly the linear decrease of void ratio (and thus increase of relative density) with increasing depth.
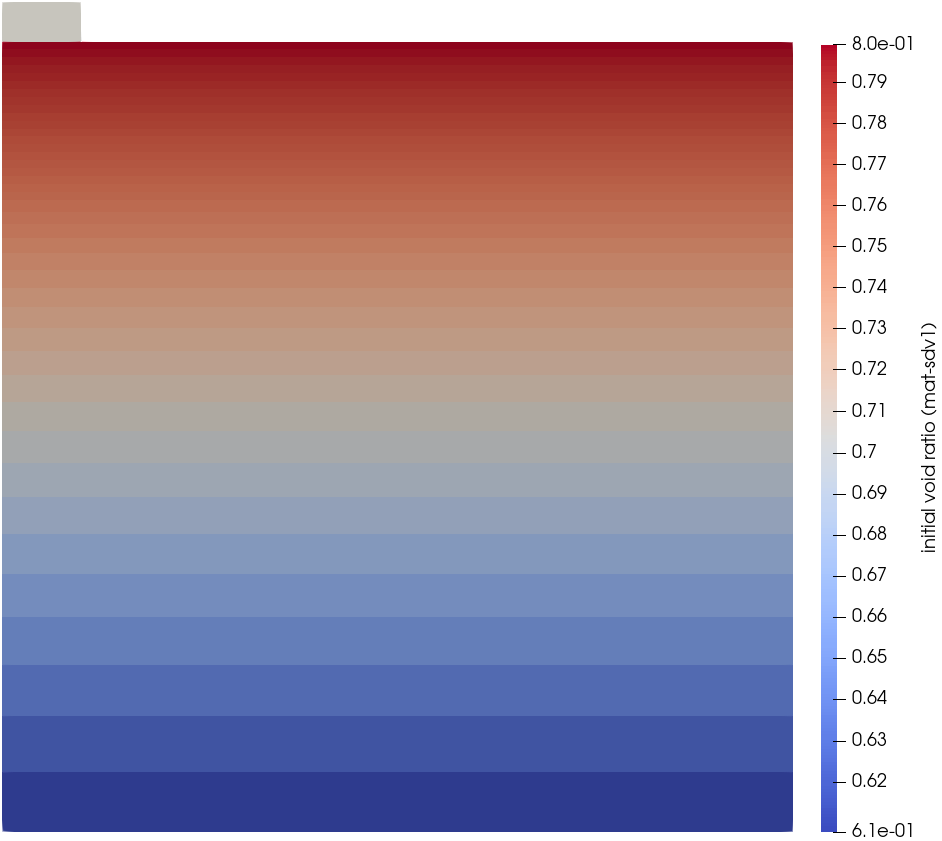
Figure 3. Initial distribution of void ratio
The shell script guiding the compilation of the user defined amplitude is as follows:
ifx -O3 /dll user_initial_state_variables.f90
#!/bin/bash
ifort -c -shared -fPIC user_initial_state_variables.f90
ifort -shared -fPIC user_initial_state_variables.o -o user_initial_state_variables.so
The simulation can now be started from the terminal using the standard procedure, e.g.
numgeo inp=input out=simulation ncpus=4
./numgeo inp=input out=simulation ncpus=4
numgeo will automatically compile the user subroutine user_material.f90 and link it to the code. The resulting settlement-time history is given in Figure 4 and compared to the reference simulation using the barotropic elasticity
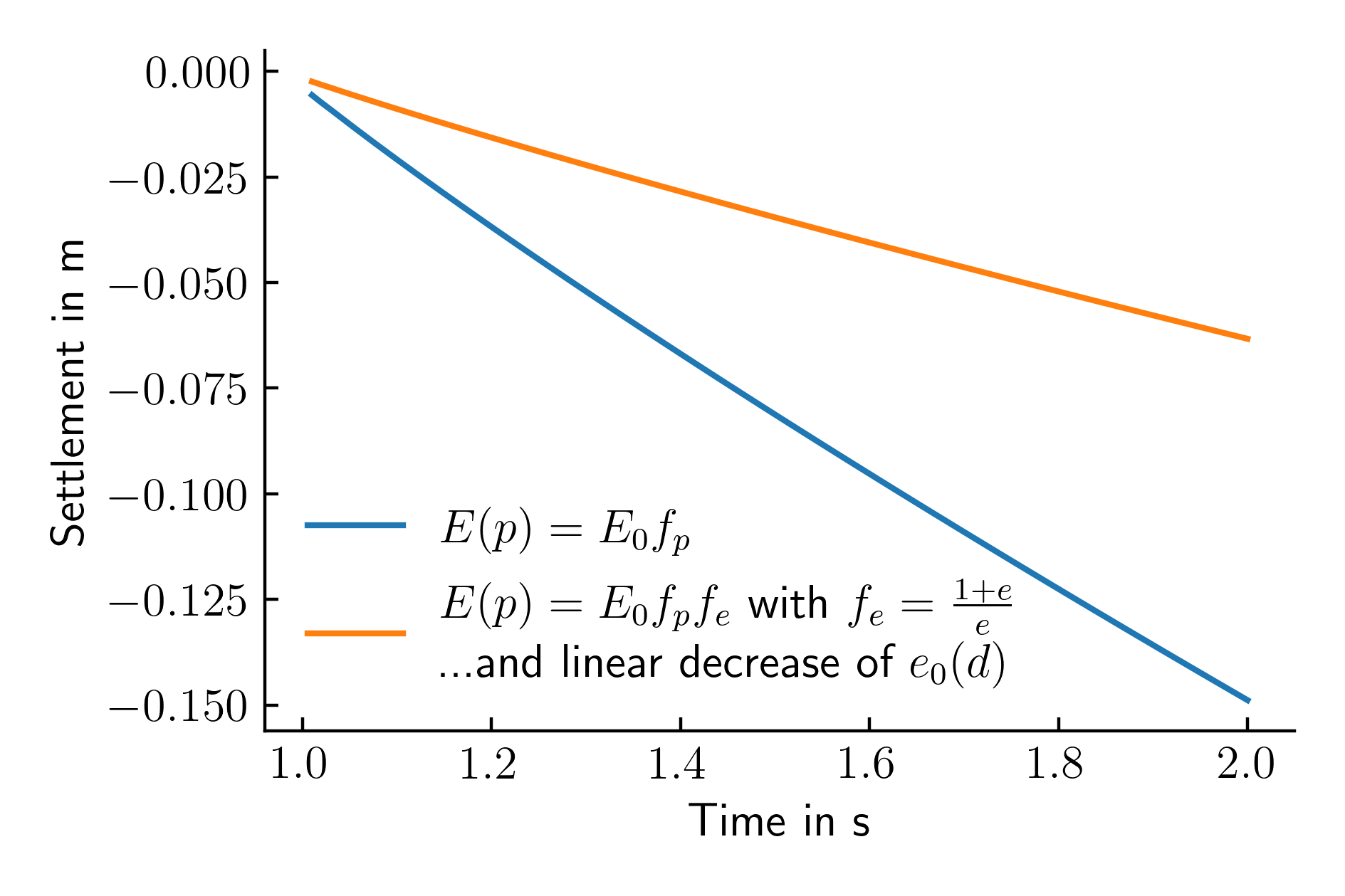
Figure 4. Settlement time history of the top left node of the shallow foundation for a linear increasing load for two different constitutive models for the soil
Plotting the results
For plotting the results as shown in above figures, the following python script can be used:
#%%
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
plt.rcParams['text.usetex'] = True
plt.rcParams['font.size'] = 12
plt.rcParams['axes.spines.right'] = False
plt.rcParams['axes.spines.top'] = False
def cm2inch(*tupl):
inch = 2.54
if isinstance(tupl[0], tuple):
return tuple(i/inch for i in tupl[0])
else:
return tuple(i/inch for i in tupl)
node_set_name = "FOUNDATION.TOP_LEFT_NODE_node_7703.dat"
ref = np.genfromtxt("./reference/simulation-print-out/"+node_set_name, skip_header=1)
data = np.genfromtxt("./user material/simulation-print-out/"+node_set_name, skip_header=1)
data2 = np.genfromtxt("./user initial state/simulation-print-out/"+node_set_name, skip_header=1)
plt.figure(figsize=cm2inch(12,8))
plt.plot(data[:,0], data[:,2], label='$E(p) = E_0 f_p$')
plt.plot(data2[:,0], data2[:,2], label='$E(p) = E_0 f_p f_e$ with $f_e=\\frac{1+e}{e}$ \n ...and linear decrease of $e_{0}(d)$')
plt.xlabel('Time in s')
plt.ylabel('Settlement in m')
plt.legend(loc='lower left', frameon=False)
plt.tight_layout()
plt.savefig('./time_settlement_user_initial_state.pdf', dpi=400)
plt.savefig('./time_settlement_user_initial_state.png', dpi=400)