Skip to content

Hypoplasticity-GIS

For the validation of the Hypo-GIS implemetation available in numgeo, a comparison with the simulation results on Zbraslav Sand reported in Mugele et al. (2024)1 is made. The Hypo-GIS implementation currently offers access to two different integration schemes:

  • Euler–Richardson — explicit scheme with adaptive substepping and error control.
  • Forward Euler — explicit scheme with a constant substep size.

Input files

The input files for the benchmark simulations can be downloaded here. The reference results were kindly provided by Luis Mugele.

We analyse an undrained cyclic triaxial test with stress amplitude \(q_{\text{ampl}} = 50\ \text{kPa}\).

The initial state is:

  • isotropic mean effective stress \(p^\prime_0 = 200\) kPa,
  • void ratio \(e_0 = 0.6915\) (relative density \(D_{r0} = 0.5\)),
  • intergranular strain \(\boldsymbol{h}_0 = \mathbf{0}\),
  • cyclic preloading variable \(\Omega_0 = 0\).

Cyclic loading is applied using the lab-cyclic-stress-strain-control amplitude, which drives the specimen at a constant strain rate of \(\dot{\varepsilon}_{ax}=10^{-6}\).

Notation: \(p^\prime\) denotes mean effective stress, \(q\) the deviatoric stress, and \(\varepsilon_{\text{ax}}\) the axial strain.

Euler Richardson (default)


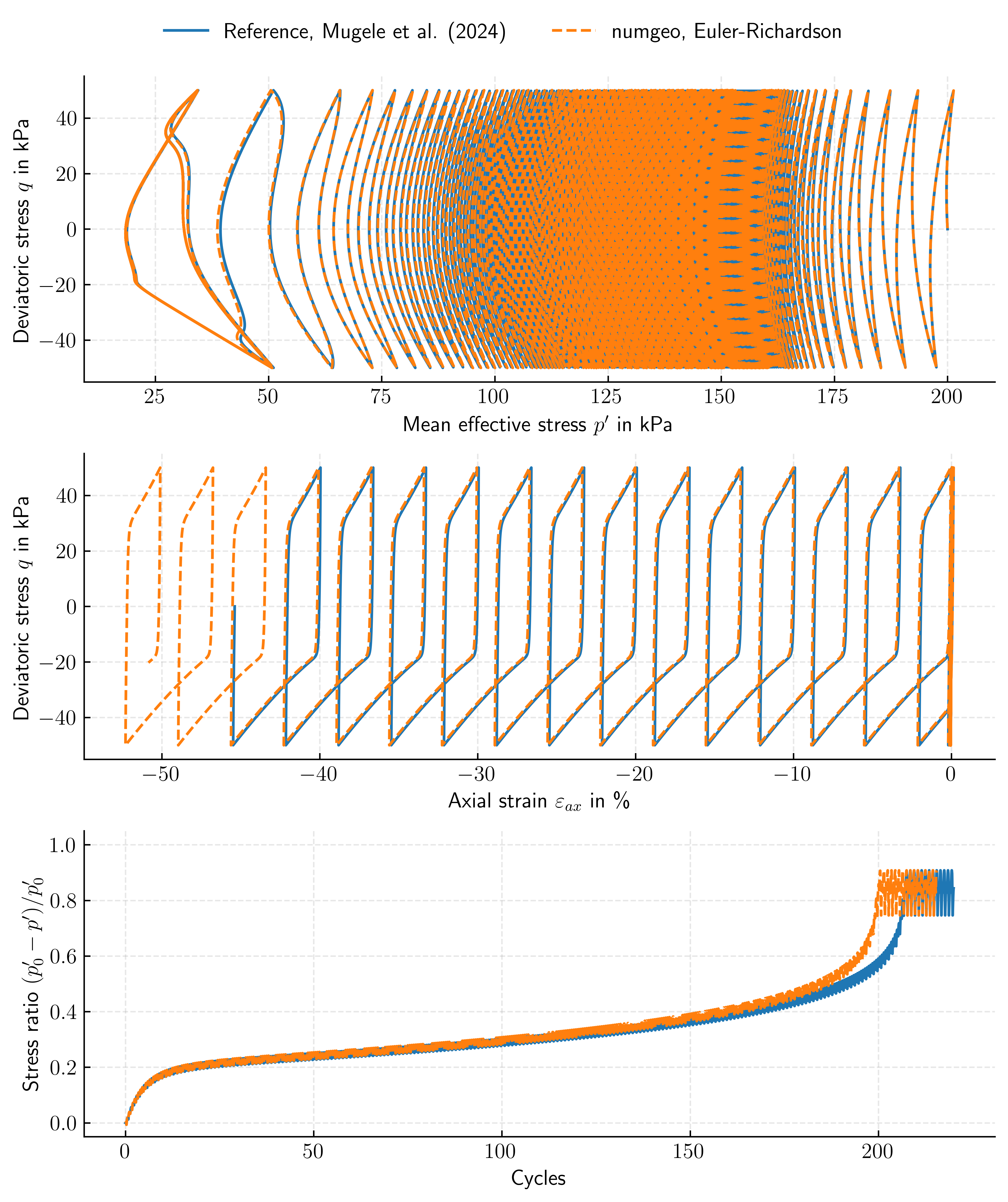
Figure 1: Undrained cyclic triaxial test — comparison of the numgeo implementation (Euler–Richardson) with the reference solution of Mugele et al. (2024)1.

The agreement between numgeo and the reference solution is very good in both the \(p'\)–\(q\) and \(\varepsilon_{\text{ax}}\)–\(q\) planes. A slightly faster accumulation of the stress ratio (e.g. \(\eta = q/p'\)) is observed in the numgeo results, which we attribute to small differences in load-path control compared with the Incremental Driver used to generate the reference curves.

Forward Euler


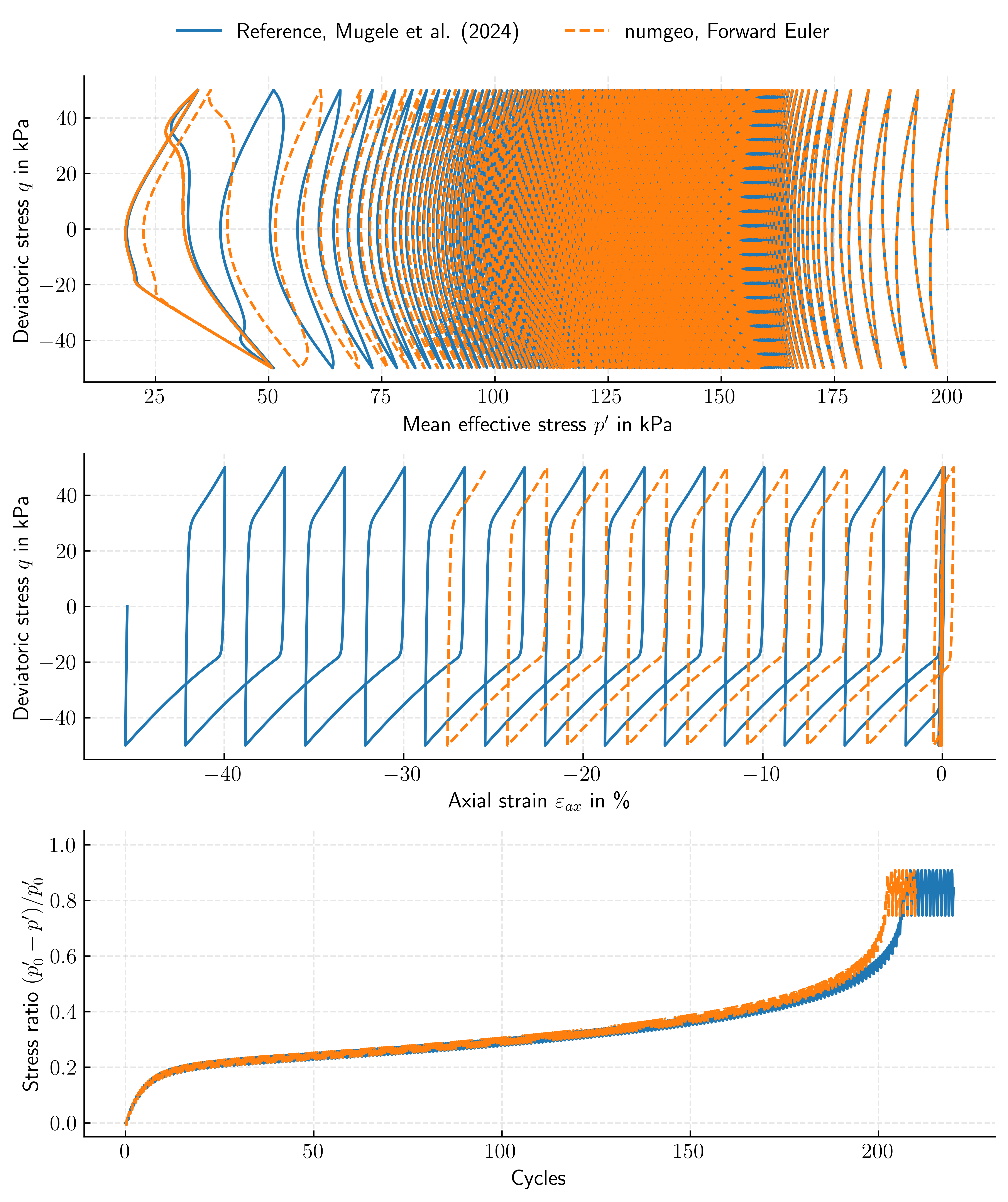
Figure 2: Undrained cyclic triaxial test — comparison of the numgeo implementation (Forward Euler) with the reference solution of Mugele et al. (2024)1.

Due to the lack of error control (and constant subincrement size) of the Forward Euler (FE) integration scheme, a ten times smaller strain rate (\(\dot{\varepsilon}_{ax}=10^{-6}\)) was used for the cyclic loading. Figure 2 shows that the general trend is captured well by the FE implementation in numgeo, however, especially when reaching the cyclic mobility phase, differences between the reference solution and the FE solution are observed.

  1. L. Mugele, H.H. Stutz, and D. Mašín. Generalized intergranular strain concept and its application to hypoplastic models. Computers and Geotechnics, 173:106480, 2024-09. doi:10.1016/j.compgeo.2024.106480. ↩↩↩