Brooks & Corey model
Governing Equation
Modified version of the original formulation of the Brooks & Corey - Mualem1 model according to Dury et al. (1999)2 :
\[\begin{align*}
k^w & = (1-k^w_{min}) \left(S^e\right)^{\frac{2+3\lambda}{\lambda}} + k^w_{min} \\
k^a &= (1-k^a_{min}) \left(1-S^e\right)^2 + k^a_{min} \left(1-\left(S^e\right)^{\frac{2+\lambda}{\lambda}}\right).
\end{align*}\]
Therein:
- \(k^{w}_{min}\) and \(k^{w}_{min}\) are the minimum relative permeability for the pore water and pore air phase, respectively.
- \(\lambda\) is the pore-size distribution index, see the hydraulic model. This dimensionless exponent reflects the uniformity of the pore sizes. A smaller \(\lambda\) value corresponds to a wider range of pore sizes, while a larger value indicates a more uniform pore structure.
The development of relative permeability \(k^\beta\) with effective degree of saturation \(S^e\) is presented here:
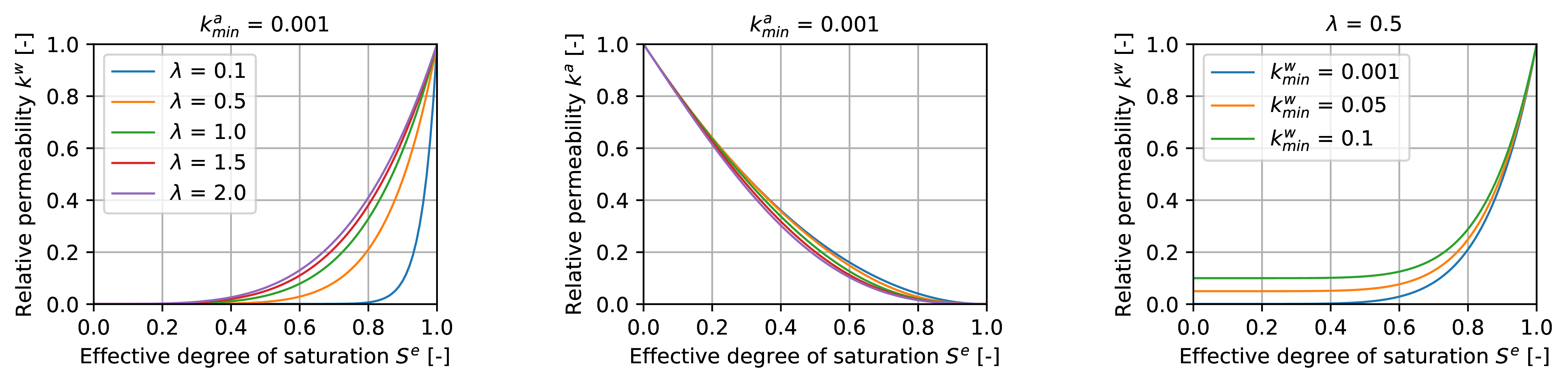
Jacobian Contribution
The contributions to the Jacobian read:
\[\begin{align*}
\frac{\partial k^w}{\partial S^e} &= (1-k^w_{min}) \frac{2+3\lambda}{\lambda} \Big(S^e\Big)^{\frac{2+3\lambda}{\lambda} - 1}, \\
\frac{\partial k^a}{\partial S^e} &= (1-k^a_{min}) \left( -2 \left(1-S^e\right) \Big( 1 - \left( S^e \right)^\frac{2+\lambda}{\lambda} \Big) - \frac{2+\lambda}{\lambda} \left(1-S^e\right)^2 \left(S^e\right)^{\frac{2+\lambda}{\lambda} - 1} \right).
\end{align*}\]
-
Reference manual
-
Yechezkel Mualem. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resources Research, 12(3):513–522, 1976. Publisher: American Geophysical Union (AGU). doi:10.1029/wr012i003p00513. ↩
-
O. Dury, U. Fischer, and R. Schulin. A comparison of relative nonwetting-phase permeability models. Water Resources Research, 35(5):1481–1493, 1999. Publisher: American Geophysical Union (AGU). doi:10.1029/1999wr900019. ↩