Drainage condition (seepage)

When the phreatic surface intersects an open, freely draining boundary (e.g. a dam face), pore fluid may drain out of the domain wherever the local pore water pressure is positive with respect to the exterior. Above the intersection point negative pore pressures can occur; their values are part of the solution.

Constitutive model on the draining surface

We model the drainage-only behaviour by prescribing an outward flux proportional to the positive excess pore pressure \(p^w\). In its classical "switch" form this reads

\[ q^w = \tilde{k}^{s}\,\langle p^w - p^w_{\text{target}}\rangle, ~~\text{where:}~~\langle x\rangle := \max(x,0), \]

which enforces no inflow when \(p^w \le p^w_{\text{target}}\) and a linear outflow when \(p^w > p^w_{\text{target}}\).

To improve Newton convergence we use a compact \(C^1\) smoothing of the Macaulay bracket. Let \(x := p^w - p^w_{\text{target}}\) and choose a small smoothing width \(\epsilon>0\) (in pressure units). Define

\[ \langle x\rangle_\epsilon = \begin{cases} 0, & x \le 0,\\ \epsilon\,(t^3 - 0.5t^4), & 0 < x < \epsilon,\\ x - 0.5\epsilon, & x \ge \epsilon \end{cases} \]

and

\[ H_\epsilon(x) := \dfrac{\mathrm{d}}{\mathrm{d}x}\langle x\rangle_\epsilon = \begin{cases} 0, & x \le 0,\\ 3t^2 - 2t^3, & 0 < x < \epsilon,\\ 1, & x \ge \epsilon, \end{cases} \]

where \(t = x/\epsilon\). The implemented boundary law is therefore

\[ q^w = \tilde{k}^{s}\,\langle p^w - p^w_{\text{target}}\rangle_\epsilon \]

with the consistent linearisation (Jacobian contribution)

\[ \dfrac{\partial q^w}{\partial p^w} = \tilde{k}^{s}\, H_\epsilon(p^w - p^w_{\text{target}}). \]

The smoothing width \(\epsilon\) should be small compared to typical positive \(p^w\) values expected on the boundary. The influence of \(\epsilon\) on \(\langle x\rangle_\epsilon\) is demonstrated in Figure 1. In numgeo \(\epsilon = 5\cdot 10^{-2}\) is used.

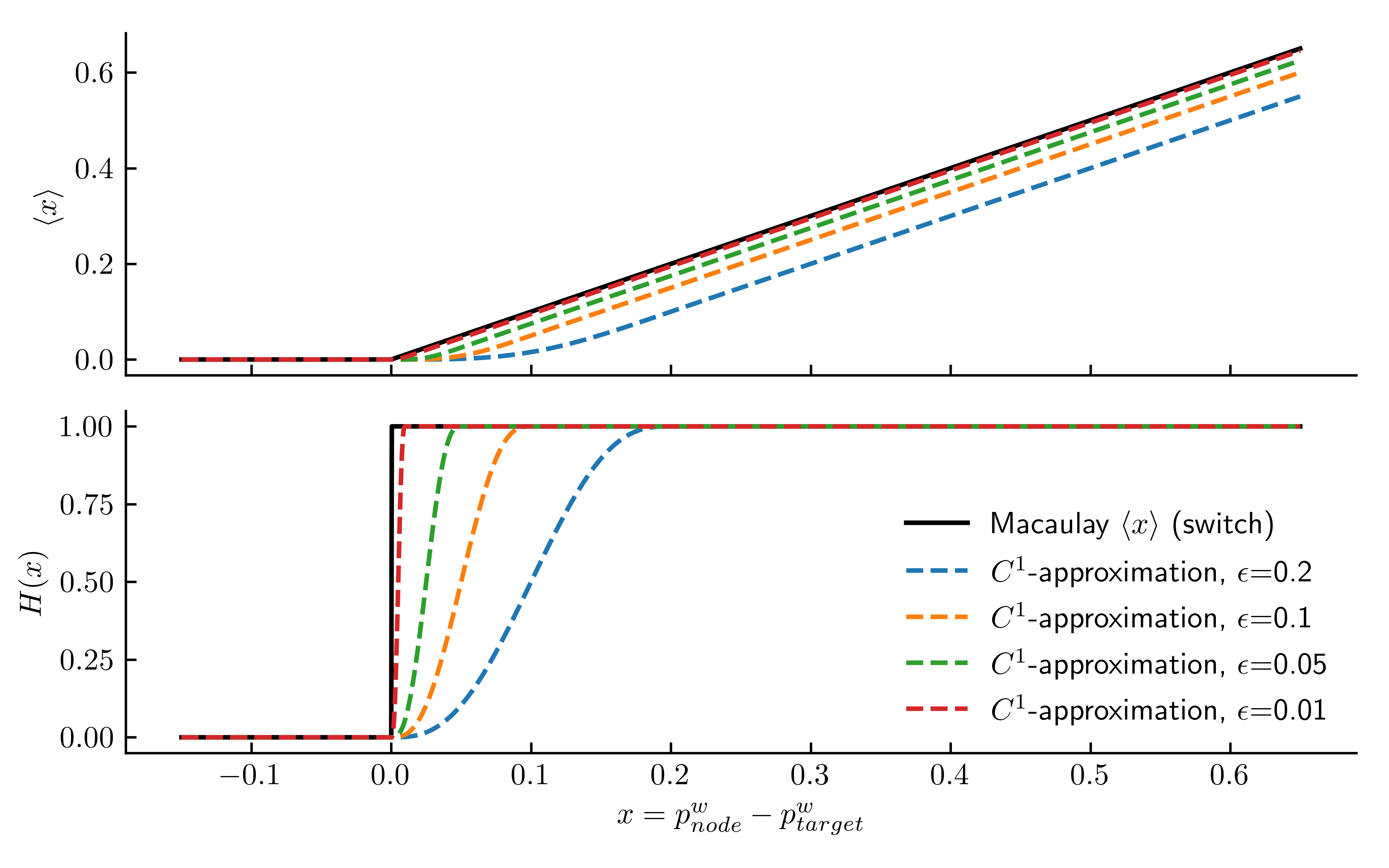
Figure 1: Comparison of the switch and the compact smoothing for different values of \(\epsilon\)

Seepage coefficient recommendations

The proportionality coefficient \(\tilde{k}^{s}\) controls how effectively the boundary drains. Little information is provided by available software on the exact choice of \(\tilde{k}^{s}\). One exception is the software Abaqus, which recommends to choose

\[ \tilde{k}^{s} = s_k_ \times \frac{k^{\text{sat}}}{\gamma_w \cdot c_E}, \]

where:

\(k^{\text{sat}}\) is the saturated hydraulic conductivity (m/s)
\(\gamma_w\) is the unit weight of water (kN/m³)
\(c_E\) is a characteristic element size below the draining face (m)
\(s_k\) = scaling factor, recommended in the order of \(10^3 - 10^5\)

Very large values of \(\tilde{k}^{s}\) may cause poor conditioning and convergence issues. Start with conservative values (\(s_k\) ≈ 1000) and increase if needed.

\(\tilde{k}^{s}\) in numgeo

With the updcoming release of numgeo, the characteristic element size \(c_E\) is automatically determined by the program. the user must thus only specify \(s_k \frac{k^{\text{sat}}}{\gamma_w}\) as parameter for the boundary condition. See also the Reference Manual.

Discrete contribution

Nodal area computation

The nodal areas \(A_i\) are computed through numerical integration over the element face:

\[ A_i = \int_{\Gamma_e} N_i\, \mathrm{d}\Gamma = \sum_{gp} N_i(\xi_{gp})\, J_{gp}\, w_{gp} \]

where \(N_i\) are the shape functions, \(J_{gp}\) is the Jacobian at Gauss point, and \(w_{gp}\) are the integration weights.

Element-specific implementation

For equal-order elements, the drainage condition is evaluated node-by-node:

\[ (f_\text{ext})_i = \tilde{k}^{s}\,A_i\,\langle p_i - p^w_{\text{target}}\rangle_\epsilon \]

\[ \frac{\partial (f_\text{ext})_i}{\partial p_j} = -\tilde{k}^{s}\,A_i\,H_\epsilon(p_i - p^w_{\text{target}})\,\delta_{ij} \]

This pointwise evaluation ensures that nodes with negative pressure contribute zero flux, respecting the physical drainage condition.

For Taylor-Hood elements, only corner nodes have pressure DOFs, and the implementation follows standard integration procedures.