Hardening Soil (MN)
This page provides a compact benchmark of the Hardening Soil (MN) implementation in numgeo using:
- (i) drained monotonic triaxial compression tests (Input files)
- (ii) undrained monotonic triaxial compression tests and (Input files)
- (iii) a vertically loaded shallow foundation (Input files).
Drained monotonic triaxial tests
The first validation exercise comprises three drained monotonic triaxial compression tests on dense Hostun sand at confining pressures of \(100\), \(300\), and \(600\) kPa. The material parameters used for these simulations are listed in Table 1.
Table 1: Hardening Soil (MN) parameters for the drained triaxial benchmark.
| Parameter | Unit | Value | Parameter | Unit | Value |
|---|---|---|---|---|---|
| \(E_{50}^{ref}\) | F/A | 30d3 | \(\nu_{ur}\) | – | 0.25 |
| \(E_{oed}^{ref}\) | F/A | 30d3 | \(p_{ref}\) | F/A | 100 |
| \(E_{ur}^{ref}\) | F/A | 90d3 | \(K_0^{nc}\) | – | 0.4 |
| \(m\) | – | 0.55 | \(R_f\) | – | 0.9 |
| \(c_{eff}\) | F/A | 0 | \(E_i^{ref}\) | F/A | 65d3 |
| \(\varphi\) | deg | 42 | \(\alpha\) | – | 0 |
| \(\psi\) | deg | 16 | \(H_{pp}\) | F/A | 0 |
The simulation results obtained with numgeo for the drained monotonic triaxial tests on dense Hostun sand are shown in Figure 1 and compared to the reference simulation results and experimental data reported in Benz (2007)1. Overall, the agreement is very good for all three confining pressures (\(100\), \(300\), and \(600\) kPa), indicating that the Hardening Soil (MN) implementation reproduces both the stress-strain response and the characteristic stiffness evolution reliably.
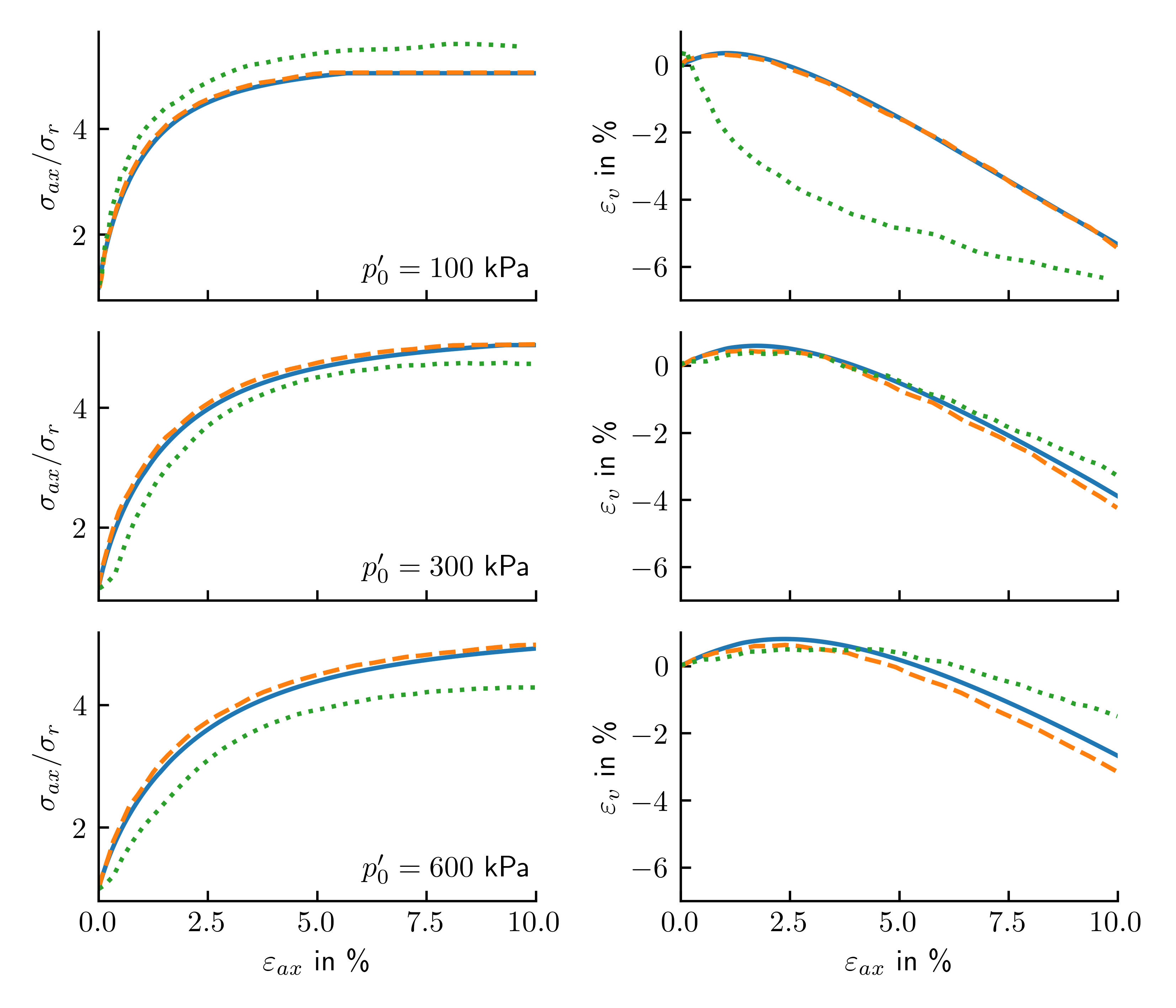 Figure 1: Drained triaxial compression tests on dense Hostun sand at confining pressures of \(100\), \(300\), and \(600\) kPa (comparison between numgeo and Benz (2007)1).
Figure 1: Drained triaxial compression tests on dense Hostun sand at confining pressures of \(100\), \(300\), and \(600\) kPa (comparison between numgeo and Benz (2007)1).
Undrained monotonic triaxial tests
The second validation exercise comprises three drained monotonic triaxial compression tests on dense Hostun sand at confining pressures of \(200\), \(300\), and \(600\) kPa. The material parameters used for these simulations are listed in Table 1.
The simulation results obtained with numgeo for the undrained monotonic triaxial tests on dense Hostun sand are shown in Figure 2 and compared to the reference simulation results and experimental data reported in Benz (2007)1. Overall, a good agreement is observed for all three confining pressures (\(200\), \(300\), and \(600\) kPa).
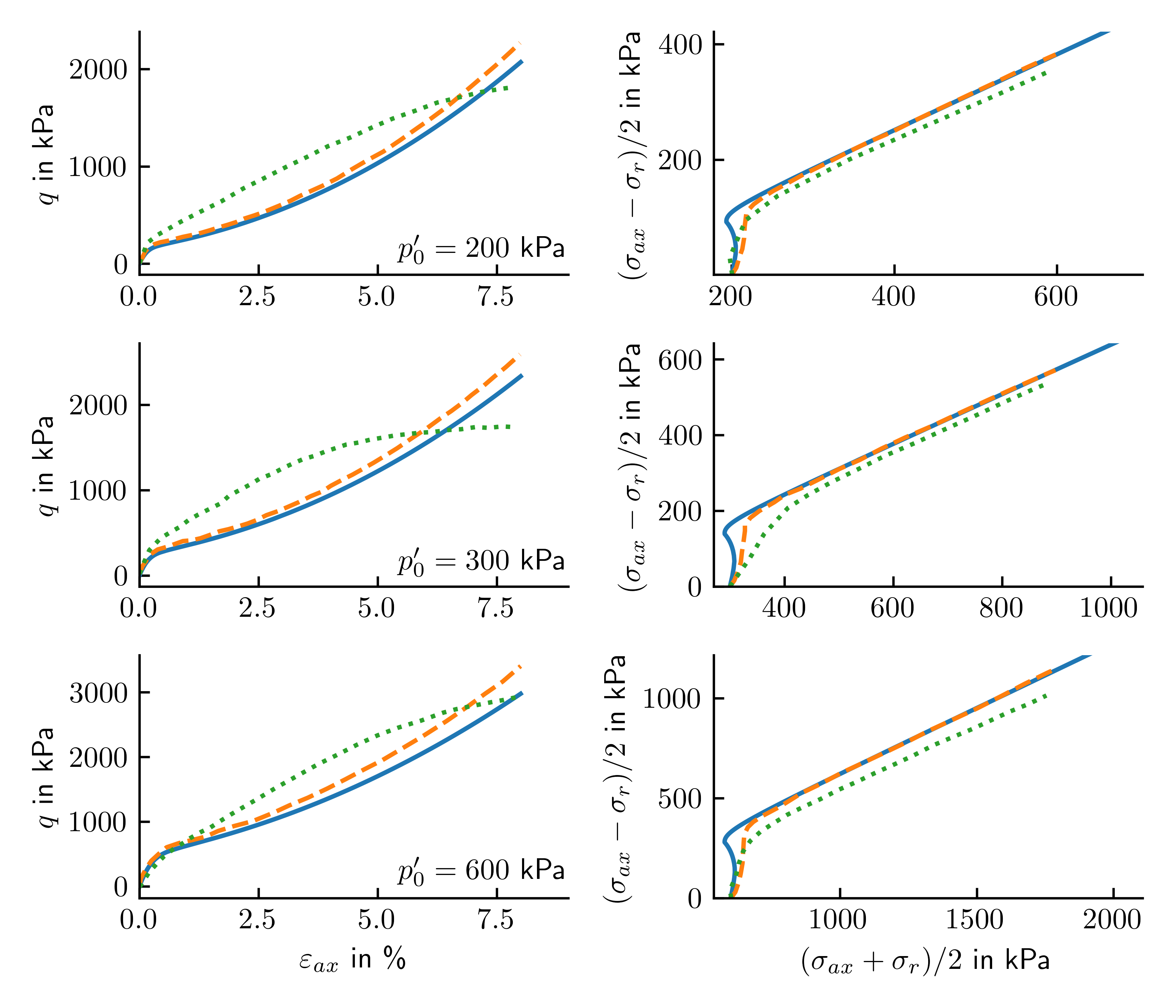 Figure 2: Undrained triaxial compression tests on dense Hostun sand at confining pressures of \(200\), \(300\), and \(600\) kPa (comparison between numgeo and Benz (2007)1).
Figure 2: Undrained triaxial compression tests on dense Hostun sand at confining pressures of \(200\), \(300\), and \(600\) kPa (comparison between numgeo and Benz (2007)1).
Shallow foundation
As a more advanced benchmark, the settlement of a circular shallow foundation under vertical loading is analysed. The finite element model has a plan size of \(10\) m \(\times 10\) m, which is sufficiently large to minimise boundary effects on the load-settlement response. The footing is idealised as a uniformly distributed pressure load of \(200\) kPa acting on a circular area with radius \(1\) m. The load is applied incrementally. The material parameters used for this benchmark are listed in Table 3.
Table 3: Hardening Soil (MN) parameters for the shallow foundation benchmark.
| Parameter | Unit | Value | Parameter | Unit | Value |
|---|---|---|---|---|---|
| \(E_{50}^{ref}\) | F/A | 30d3 | \(\nu_{ur}\) | – | 0.25 |
| \(E_{oed}^{ref}\) | F/A | 30d3 | \(p_{ref}\) | F/A | 100 |
| \(E_{ur}^{ref}\) | F/A | 90d3 | \(K_0^{nc}\) | – | 0.4 |
| \(m\) | – | 0.55 | \(R_f\) | – | 0.9 |
| \(c_{eff}\) | F/A | 0 | \(E_i^{ref}\) | F/A | 54.55d3 |
| \(\varphi\) | deg | 42 | \(\alpha\) | – | 0 |
| \(\psi\) | deg | 16 | \(H_{pp}\) | F/A | 0 |
The computed load-settlement response of the circular shallow foundation is presented in Figure 3 and compared to the corresponding reference simulation obtained with PLAXIS. The numgeo curve matches the reference response very well over the full loading path, demonstrating that the model implementation provides an accurate prediction of the nonlinear settlement development under incremental vertical loading.
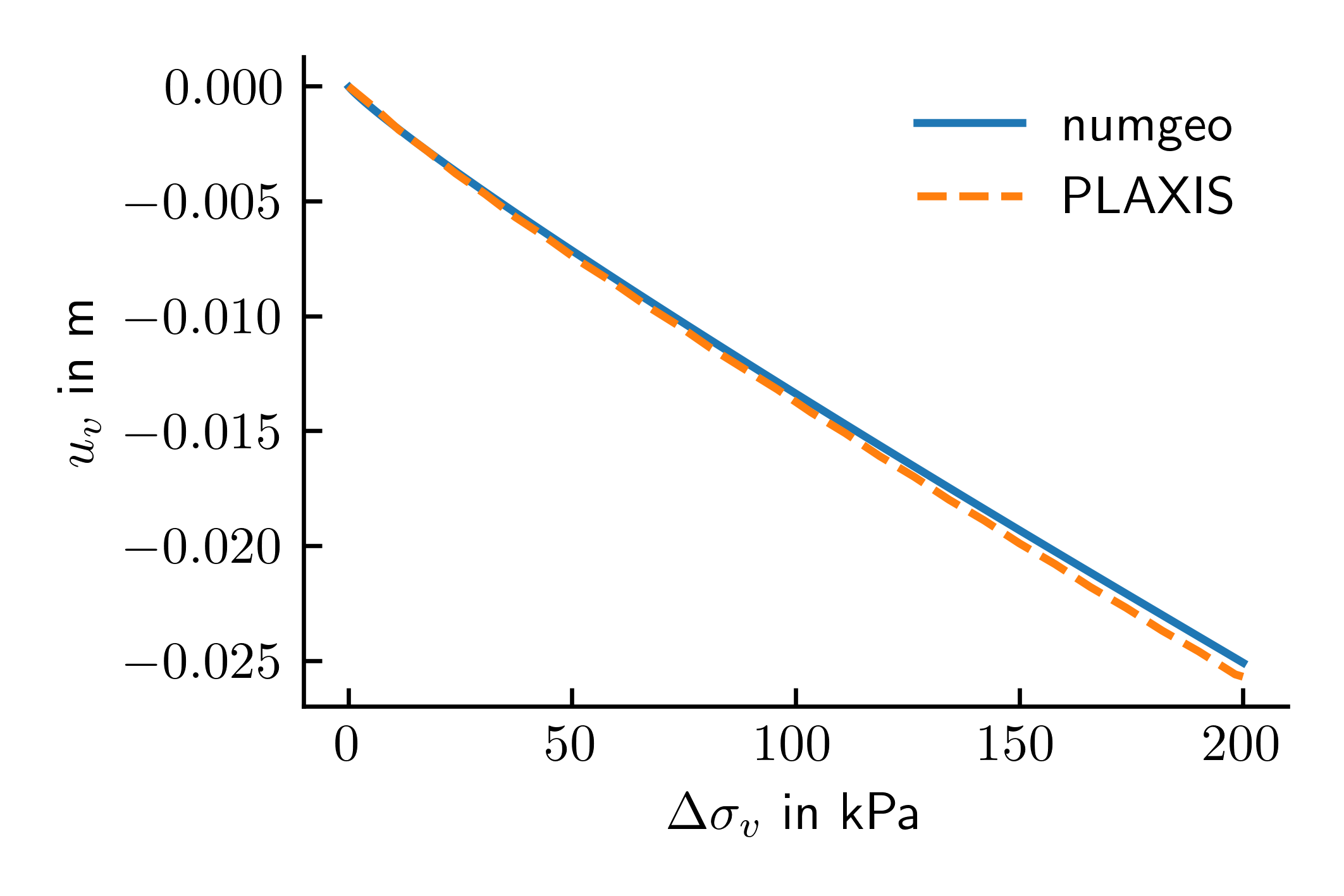 Figure 3: Load-settlement response of the circular shallow foundation under vertical loading (comparison between numgeo and PLAXIS).
Figure 3: Load-settlement response of the circular shallow foundation under vertical loading (comparison between numgeo and PLAXIS).
-
Thomas Benz. Small-Strain Stiffness of Soils and Its Numerical Consequences. PhD thesis, Inst. für Geotechnik, 2007. URL: https://www.igs.uni-stuttgart.de/dokumente/Mitteilungen/55_Benz.pdf. ↩↩↩↩