Nonlinear Geometry: Single-Element tests
This benchmark verifies the nonlinear geometry (nlgeom) implementation in numgeo by direct comparison with Abaqus reference solutions. The objective is to validate the geometric formulation independently of mesh effects, numerical locking, or constitutive-model-specific artefacts.
The comparison is performed using a single finite element subjected to prescribed displacement fields that induce large strains, large rotations, and rigid body motions.
1. Scope and objective
The benchmark addresses two distinct classes of constitutive formulations:
-
Hyperelastic materials (Neo-Hookean):
- stress is derived directly from a strain energy function,
- no incremental stress update is required,
- Hughes–Winget is not used.
-
Incremental (rate-type) constitutive models:
- nonlinear geometry handled via the Hughes–Winget algorithm,
- linear elasticity formulated and integrated incrementally,
- used to validate the general
nlgeominfrastructure for rate-form material models.
The purpose of this benchmark is therefore twofold:
- verify the finite-strain kinematics for hyperelastic materials, and
- verify the Hughes–Winget-based geometric update for incremental constitutive models.
2. Element geometry and discretisation
A single quadrilateral element with linear interpolation and full integration is used throughout. The element has dimensions \(1.0 \times 1.0\ \text{m}\) and is evaluated in plane strain and axisymmetric settings.
The nodal coordinates are:
- node 1: \((0.0, 0.0)\)
- node 2: \((1.0, 0.0)\)
- node 3: \((1.0, 1.0)\)
- node 4: \((0.0, 1.0)\)
All simulations employ linear shape functions, four Gauss integration points, identical element orientation and node numbering in numgeo and Abaqus.
3. Investigated load cases
Six kinematically prescribed deformation modes are investigated. For plane strain, all six cases are analysed. For axisymmetric elements, only Cases 1-4 are applicable.
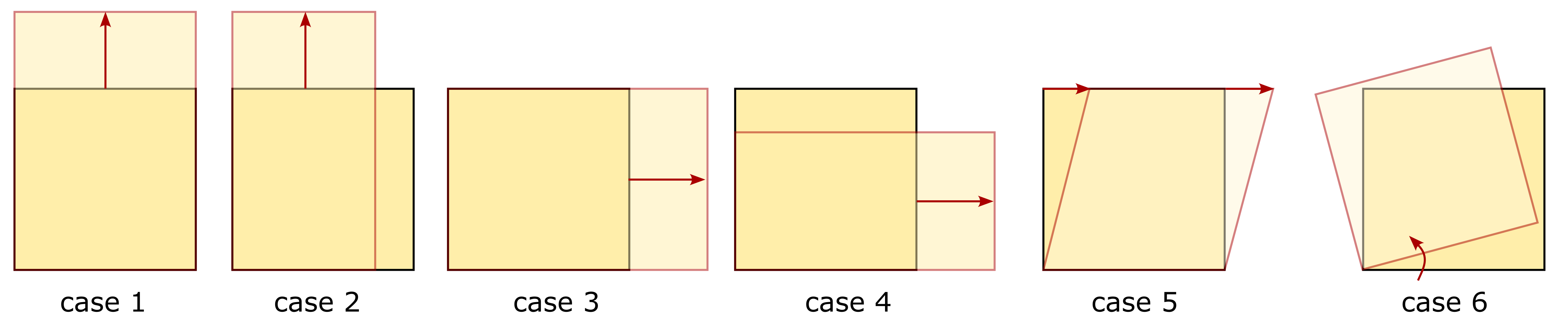
Figure 1. Different load/deformation cases considered in the benchmark simulations
The cases are defined as follows:
-
Vertical extension (horizontally fixed): Top nodes displaced vertically by \(+1.0\ \text{m}\); horizontal displacements fixed.
-
Vertical extension (horizontally free): As Case 1, but right-hand nodes free in the horizontal direction.
-
Horizontal extension (vertically fixed): Right-hand nodes displaced horizontally by \(+1.0\ \text{m}\); top nodes fixed vertically.
-
Horizontal extension (vertically free): As Case 3, but top nodes free in the vertical direction.
-
Simple shear: Top nodes displaced horizontally by \(+0.5\ \text{m}\); vertical displacements fixed.
-
Rigid body rotation: Approximate rigid rotation of the element by \(30^\circ\) about the point \((0,0)\), realised by prescribing nodal displacements with finite numerical precision.
4. Numerical design considerations
The prescribed deformation modes are chosen such that:
- no volumetric, shear, or bending locking can occur,
- no sensitivity to integration scheme or element formulation exists,
- differences between numgeo and Abaqus can only originate from the geometric implementation.
The rigid body rotation case is realised via prescribed displacements with finite numerical accuracy. As a consequence, small stress magnitudes are expected, but these stresses are identical in Abaqus and numgeo.
Input files
The input files to reproduce this benchmark can be downloaded here.
6. Results and comparison
The above introduced combination of constitutive models and load cases results in a total of 20 benchmark simulations. The results of which are provided in the following subsections. The results are reported by means of the sum of reaction forces \(RF\) and displacements \(u\) in horizontal (\(\sqcup_1\)) and vertical (\(\sqcup_2\)) direction. For the cases 1, 2, 5 and 6, the top nodes have been evaluated while nodes on the right side of the element have been considered for the cases 3 and 4.
Plane strain, Neo-Hooke
Plane strain, Linear elastic
Axisymmetric, Neo-Hooke
Axisymmetric, Linear elastic
7. Conclusions
The benchmark confirms that the nonlinear geometry (nlgeom) implementation in numgeo:
- is correct for finite-strain hyperelastic materials,
- correctly applies the Hughes–Winget algorithm for incremental constitutive models,
- handles large rotations and rigid body motions consistently,
- reproduces Abaqus reference solutions exactly for all investigated cases.